10.2 – Autokorrelation und Zeitreihenmethoden

Eine häufige Art und Weise, wie die Bedingung der „Unabhängigkeit“ in einem multiplen linearen Regressionsmodell versagen kann, ist, wenn die Stichprobendaten im Laufe der Zeit gesammelt wurden und das Regressionsmodell nicht in der Lage ist, irgendwelche Zeittrends effektiv zu erfassen. In einem solchen Fall sind die zufälligen Fehler im Modell im Laufe der Zeit oft positiv korreliert, so dass jeder zufällige Fehler mit größerer Wahrscheinlichkeit dem vorherigen zufälligen Fehler ähnelt, als es der Fall wäre, wenn die zufälligen Fehler unabhängig voneinander wären. Dieses Phänomen ist als Autokorrelation (oder serielle Korrelation) bekannt und kann manchmal durch das Auftragen der Modellresiduen über die Zeit erkannt werden. Wir werden dies in diesem und im nächsten Abschnitt näher untersuchen.

Eine Zeitreihe ist eine Folge von Messungen der gleichen Variable(n), die im Laufe der Zeit vorgenommen wurden. Normalerweise werden die Messungen in gleichmäßigen Zeitabständen vorgenommen – zum Beispiel monatlich oder jährlich. Betrachten wir zunächst das Problem, in dem wir eine y-Variable als Zeitreihe gemessen haben. Als Beispiel könnte y ein Maß für die globale Temperatur sein, mit Messungen, die jedes Jahr beobachtet werden. Um zu betonen, dass wir Messwerte über die Zeit haben, verwenden wir „t“ als tiefgestellten Index anstelle des üblichen „i“, d. h. \(y_t\) bedeutet \(y\) gemessen im Zeitraum \(t\). Ein autoregressives Modell liegt vor, wenn ein Wert aus einer Zeitreihe auf frühere Werte aus derselben Zeitreihe regressiert wird. z. B. \(y_{t}\) auf \(y_{t-1}\):

In diesem Regressionsmodell ist die Antwortvariable in der vorherigen Zeitperiode zum Prädiktor geworden und die Fehler haben unsere üblichen Annahmen über Fehler in einem einfachen linearen Regressionsmodell. Die Ordnung einer Autoregression ist die Anzahl der unmittelbar vorangehenden Werte in der Reihe, die zur Vorhersage des Wertes zum aktuellen Zeitpunkt verwendet werden. Das vorangegangene Modell ist also eine Autoregression erster Ordnung, geschrieben als AR(1).

Wenn wir \(y\) in diesem Jahr (\(y_{t}\)) anhand der Messungen der globalen Temperatur in den beiden vorangegangenen Jahren (\(y_{t-1},y_{t-2}\)) vorhersagen wollen, dann wäre das autoregressive Modell dafür:

Dieses Modell ist eine Autoregression zweiter Ordnung, geschrieben als AR(2), da der Wert zum Zeitpunkt $t$ aus den Werten zu den Zeitpunkten \(t-1\) und \(t-2\) vorhergesagt wird. Allgemeiner ausgedrückt, ist eine Autoregression \(k^{\textrm{th}})-Ordnung, geschrieben als AR(k), eine multiple lineare Regression, bei der der Wert der Reihe zu jedem Zeitpunkt t eine (lineare) Funktion der Werte zu den Zeitpunkten \(t-1,t-2,\ldots,t-k\) ist.

Autokorrelation und partielle Autokorrelation

Der Korrelationskoeffizient zwischen zwei Werten in einer Zeitreihe wird Autokorrelationsfunktion (ACF) genannt. Zum Beispiel ist die ACF für eine Zeitreihe \(y_t\) gegeben durch:

Der Wert von k ist der betrachtete Zeitabstand und wird Lag genannt. Eine Lag-1-Autokorrelation (d. h. k = 1 in der obigen Darstellung) ist die Korrelation zwischen Werten, die eine Zeitperiode auseinander liegen. Allgemeiner ausgedrückt ist eine Lag-k-Autokorrelation die Korrelation zwischen Werten, die k Zeitperioden auseinander liegen.

Der ACF ist eine Möglichkeit, die lineare Beziehung zwischen einer Beobachtung zum Zeitpunkt t und den Beobachtungen zu früheren Zeitpunkten zu messen. Wenn wir ein AR(k)-Modell annehmen, dann möchten wir vielleicht nur den Zusammenhang zwischen \(y_{t}\) und \(y_{t-k}\) messen und den linearen Einfluss der dazwischen liegenden Zufallsvariablen herausfiltern (d.h. \(y_{t-1},y_{t-2},\ldots,y_{t-(k-1 )}\)), was eine Transformation der Zeitreihe erfordert. Durch die Berechnung der Korrelation der transformierten Zeitreihen erhalten wir dann die partielle Autokorrelationsfunktion (PACF).

Die PACF ist sehr nützlich, um die Ordnung eines autoregressiven Modells zu identifizieren. Insbesondere zeigen partielle Autokorrelationen der Stichprobe, die sich signifikant von 0 unterscheiden, verzögerte Terme von \(y\) an, die nützliche Prädiktoren von \(y_{t}\) sind. Es ist wichtig, dass die Wahl der Reihenfolge sinnvoll ist. Nehmen wir zum Beispiel an, Sie haben Blutdruckmesswerte für jeden Tag in den letzten zwei Jahren. Sie könnten feststellen, dass ein AR(1)- oder AR(2)-Modell für die Modellierung des Blutdrucks geeignet ist. Der PACF kann jedoch einen großen partiellen Autokorrelationswert bei einer Verzögerung von 17 anzeigen, aber eine so große Ordnung für ein autoregressives Modell macht wahrscheinlich nicht viel Sinn.

Beispiel 1: Google-Daten

Der Datensatz (google_stock.txt) besteht aus n = 105 Werten, die den Schlusskurs einer Aktie von Google im Zeitraum vom 2.7.2005 bis zum 7.7.2005 darstellen. Wir werden den Datensatz analysieren, um die Ordnung eines autoregressiven Modells zu identifizieren. Ein Diagramm der Aktienkurse gegen die Zeit ist in der folgenden Abbildung dargestellt:

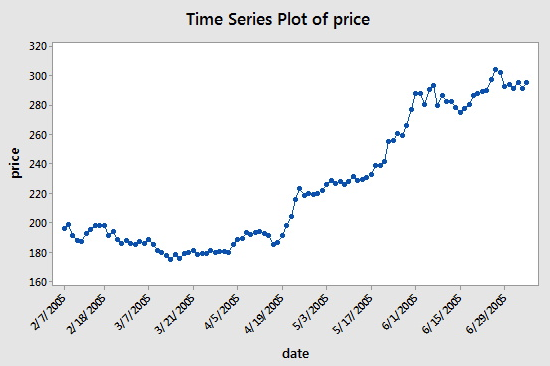
Die aufeinanderfolgenden Werte scheinen einander ziemlich genau zu folgen, was darauf hindeutet, dass ein Autoregressionsmodell angemessen sein könnte. Als nächstes sehen wir uns ein Diagramm der partiellen Autokorrelationen für die Daten an:

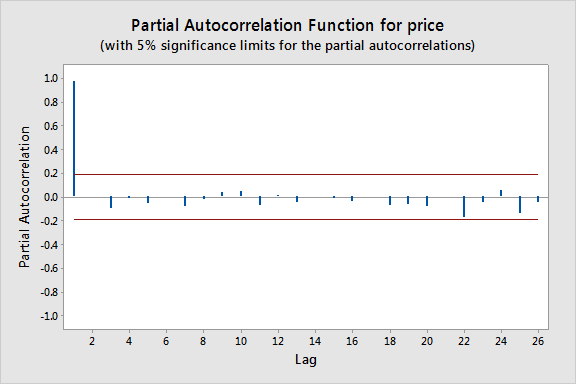
Hier sehen wir, dass es eine signifikante Spitze bei einer Verzögerung von 1 gibt und viel geringere Spitzen für die nachfolgenden Verzögerungen. Daher wäre ein AR(1)-Modell für diesen Datensatz wahrscheinlich realisierbar.

Auch für dieses Diagramm können ungefähre Grenzen konstruiert werden (wie durch die roten Linien im obigen Diagramm angegeben), um bei der Bestimmung großer Werte zu helfen. Ungefähre \((1-\alpha)\mal 100\%\) Signifikanzgrenzen sind durch \(\pm z_{1-\alpha/2}/\sqrt{n}\) gegeben. Werte, die außerhalb einer dieser Schranken liegen, deuten auf einen autoregressiven Prozess hin.

Als nächstes erstellen wir eine Lag-1-Preisvariable und betrachten ein Streudiagramm des Preises gegen diese Lag-1-Variable:

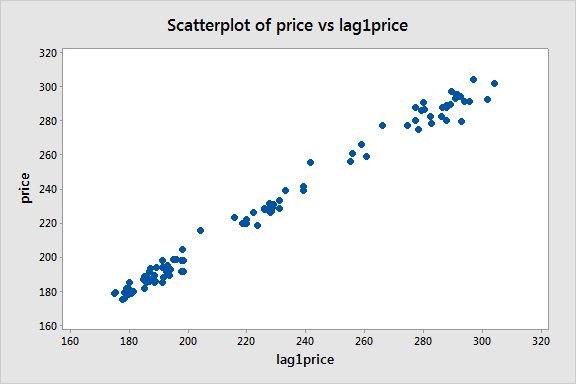
Es scheint ein starkes lineares Muster zu geben, was bestätigt, dass das Modell der Autoregression erster Ordnung

dabei nützlich sein könnte.

Beispiel 2: Erdbebendaten

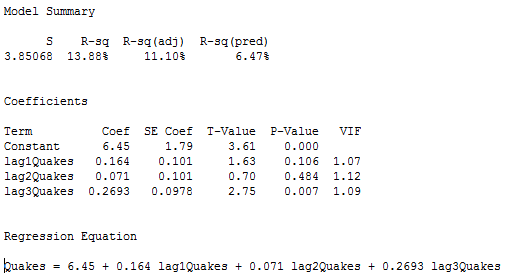
Lassen Sie yt = die jährliche Anzahl der weltweiten Erdbeben mit einer Stärke von mehr als 7 auf der Richterskala für n = 100 Jahre (Daten von earthquakes.txt, erhalten von https://earthquake.usgs.gov). Der folgende Plot zeigt eine Zeitreihendarstellung für diesen Datensatz.

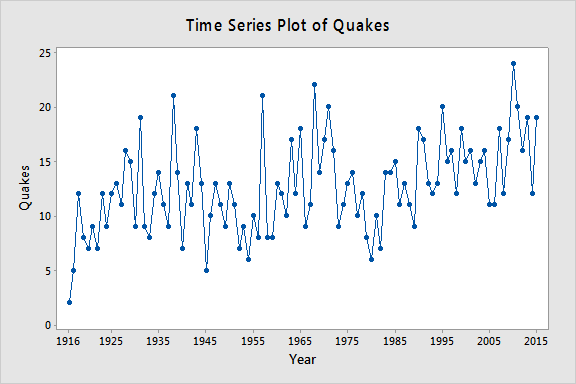
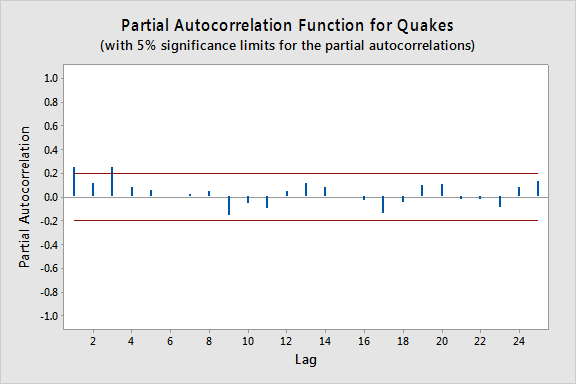
Der Plot unten zeigt einen Plot der PACF (partielle Autokorrelationsfunktion), der dahingehend interpretiert werden kann, dass eine Autoregression dritter Ordnung gerechtfertigt sein könnte, da es bemerkenswerte partielle Autokorrelationen für Lags 1 und 3 gibt.

Der nächste Schritt ist die Durchführung einer multiplen linearen Regression mit der Anzahl der Beben als Antwortvariable und Lag-1, Lag-2 und Lag-3 Beben als Prädiktorvariablen. In den Ergebnissen unten sehen wir, dass der lag-3 Prädiktor auf dem 0,05-Niveau signifikant ist (und der p-Wert des lag-1 Prädiktors ist auch relativ klein).