3.7 – Power Analysis
Nach Abschluss eines statistischen Tests werden Rückschlüsse auf die Nullhypothese gezogen. In Fällen, in denen die Nullhypothese nicht verworfen wird, kann ein Forscher immer noch der Meinung sein, dass die Behandlung einen Effekt hatte. Nehmen wir an, dass drei Behandlungen zur Gewichtsabnahme durchgeführt werden. Am Ende der Studie analysiert der Forscher die Daten und stellt fest, dass es keine Unterschiede zwischen den Behandlungen gibt. Der Forscher glaubt, dass es tatsächlich Unterschiede gibt. Während Sie vielleicht denken, dass dies nur Wunschdenken des Forschers ist, könnte es einen statistischen Grund für das Fehlen signifikanter Ergebnisse geben.
An diesem Punkt kann der Forscher eine Power-Analyse durchführen. Erinnern Sie sich an Ihren einführenden Text oder Kurs, dass Power die Fähigkeit ist, die Null zurückzuweisen, wenn die Null wirklich falsch ist. Die Faktoren, die sich auf die Potenz auswirken, sind die Stichprobengröße (größere Stichproben führen zu mehr Potenz), die Effektgröße (Behandlungen, die zu größeren Unterschieden zwischen den Gruppen führen, haben Unterschiede, die leichter gefunden werden), die Variabilität des Experiments und die Signifikanz des Typ-1-Fehlers.
Zu beachten ist, dass die häufigste Art von Potenzanalysen diejenigen sind, die die erforderlichen Stichprobengrößen für experimentelle Designs berechnen. Bei diesen Analysen werden Pilotdaten oder frühere Untersuchungen herangezogen. Wenn die Power-Analyse im Voraus durchgeführt wird, handelt es sich um eine PROSPEKTIVE Power-Analyse. In unserem Beispiel ist die Verwendung einer Power-Analyse, nachdem das Experiment durchgeführt wurde, eine retrospektive Power-Analyse.
Zurück zu unserem Beispiel. Normalerweise wollen wir eine Power von 80 % haben. Wiederum stellt die Potenz unsere Fähigkeit dar, die Null zurückzuweisen, wenn sie falsch ist, also bedeutet eine Potenz von 80 %, dass wir dies in 80 % der Fälle richtig machen. Im Umkehrschluss bedeutet dies, dass wir in 20 % der Fälle riskieren, den Nullwert nicht abzulehnen, obwohl wir den Nullwert eigentlich ablehnen sollten.
Anhand unseres Beispiels mit dem Gewächshaus können wir eine retrospektive Power-Analyse durchführen (nur zur Erinnerung: Wir führen dies normalerweise nicht durch, es sei denn, wir haben einen Grund zu der Annahme, dass die Power unseres Tests sehr niedrig war). Dies ist eine Analyse, bei der Minitab viel einfacher und dennoch genauso genau wie SAS ist, daher werden wir Minitab verwenden, um diese einfache Power-Analyse zu veranschaulichen.
Minitab: Power-Analyse
Mit den folgenden Screenshots können Sie das Power-Menü in Minitab aufrufen.
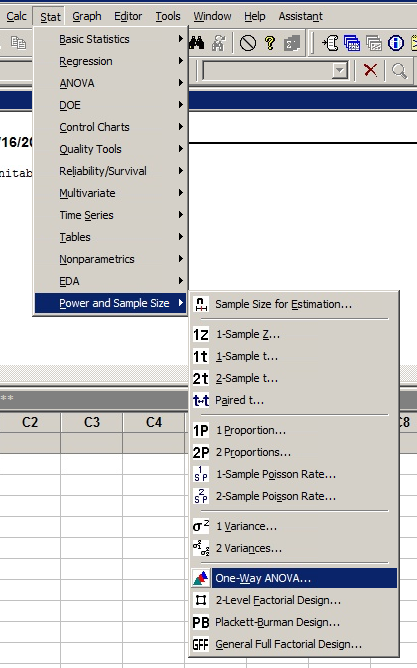
Da es sich um eine einseitige ANOVA handelt, wählen wir diesen Test aus (wie Sie sehen, gibt es Power-Analysen für viele verschiedene Tests, und SAS erlaubt sogar noch kompliziertere Optionen)
Als Nächstes fragt das Dialogfeld nach den vier oben beschriebenen Elementen.
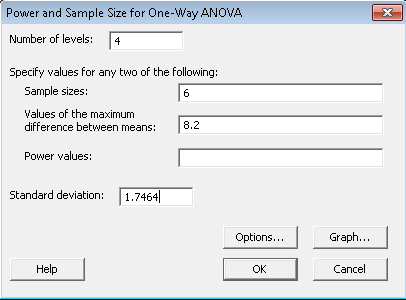
Wenn Sie sich unser ausgefülltes Dialogfeld ansehen, fällt Ihnen auf, dass wir keinen Wert für die Potenz eingegeben haben. Das liegt daran, dass Minitab das Feld berechnet, das Sie leer lassen. Wenn wir also den Stichprobenumfang benötigen, würden wir den Stichprobenumfang leer lassen und einen Wert für die Potenz eingeben. Aus unserem Beispiel wissen wir, dass die Anzahl der Ebenen 4 beträgt, da wir vier Behandlungen haben. Wir haben sechs Beobachtungen für jede Behandlung, also ist der Stichprobenumfang 6. Der Wert für die maximale Differenz der Mittelwerte ist 8,2 (wir haben einfach den kleinsten Mittelwert vom größten Mittelwert subtrahiert, und die Standardabweichung ist 1,747. Woher kommt das? Der MSE stellt den Fehler im Modell dar. Wir betrachten den MSE auch als die Variabilität im Modell. Um die Standardabweichung zu erhalten, nehmen wir einfach die Quadratwurzel aus dem MSE (in diesem Fall war der MSE ungefähr 3).
Nachdem wir auf OK klicken, erhalten wir die folgende Ausgabe:
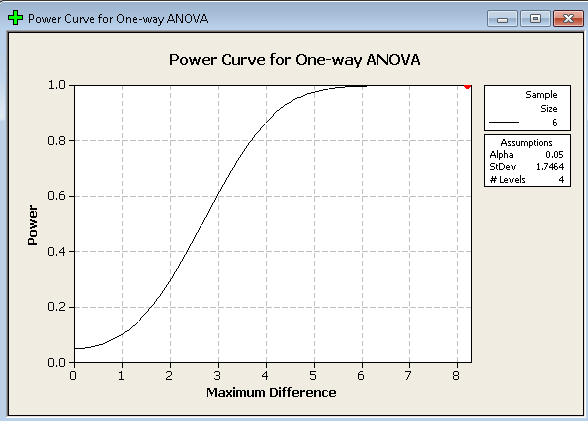
Wenn Sie diese Grafik verfolgen, sehen Sie, dass die Power auf der y-Achse liegt. Da wir daran interessiert sind, zu bestimmen, wie hoch die Leistung des Beispiels mit dem grünen Haus ist, müssen wir nur den kleinen roten Punkt im Diagramm finden. Er ist schwer zu finden, aber wenn man genau hinschaut, entspricht der rote Punkt einer Potenz von 1. Das ist sehr ungewöhnlich, lässt sich aber leicht damit erklären, dass die Gewächshausdaten zusammengestellt wurden, um Unterschiede zu zeigen.
Wir können die Frage stellen, wie es mit den Unterschieden zwischen den Behandlungsgruppen aussieht, ohne die Kontrolle zu berücksichtigen. Alles, was wir tun müssen, ist, einige der Eingaben in Minitab zu ändern.
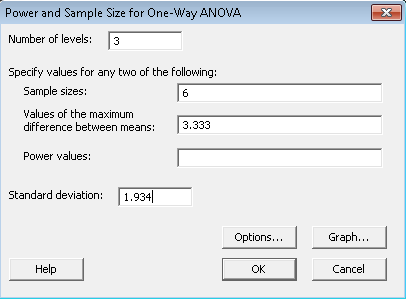
Beachten Sie hier die Unterschiede zum vorherigen Bildschirmfoto. Wir haben jetzt 3 Ebenen, weil wir nur die drei Behandlungen betrachten. Die maximalen Unterschiede zwischen den Mittelwerten und auch die Standardabweichung sind ebenfalls unterschiedlich.
Die Ausgabe ist jetzt viel einfacher zu sehen:
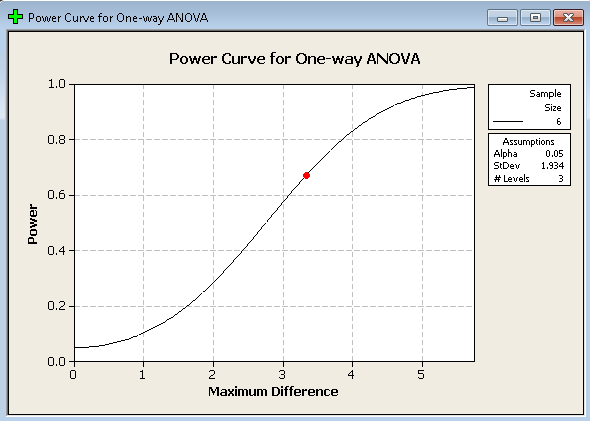
Hier können wir sehen, dass die Leistung geringer ist als bei Einbeziehung der Kontrolle. Der Hauptgrund für diese Abnahme ist, dass der Unterschied zwischen den Mittelwerten kleiner ist.
Sie können mit der Potenzfunktion in Minitab experimentieren, um sich Stichprobengrößen usw. für verschiedene Potenzen anzeigen zu lassen. Unten sehen Sie einige Beispielausgaben, wenn wir nach verschiedenen Potenzkurven für verschiedene Stichprobengrößen fragen, eine Art „Was-wäre-wenn“-Szenario.
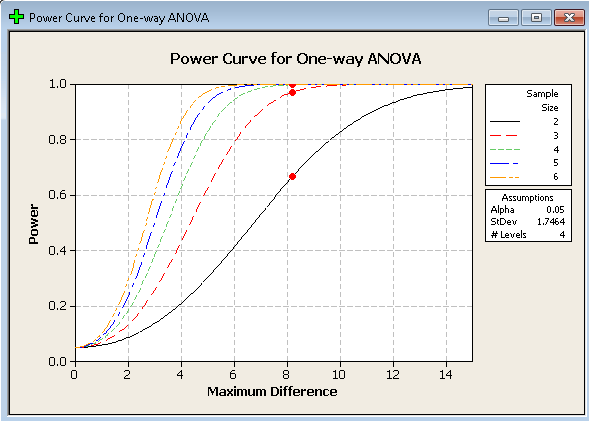
Nur zur Erinnerung: Potenzanalysen werden meistens VOR der Durchführung eines Experiments durchgeführt, aber gelegentlich kann eine Potenzanalyse Hinweise darauf liefern, warum keine signifikanten Unterschiede gefunden wurden.