Anwendungen von Operationsverstärkern

Das erste Beispiel ist der Differenzverstärker, von dem sich viele der anderen Anwendungen ableiten lassen, darunter der invertierende, nichtinvertierende und summierende Verstärker, der Spannungsfolger, Integrator, Differenzierer und Gyrator.

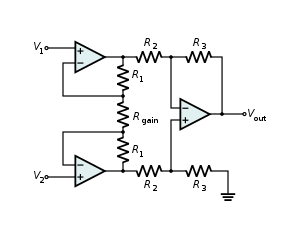
Differenzverstärker (Differenzverstärker)

Hauptartikel: Differenzverstärker

Verstärkt die Spannungsdifferenz zwischen seinen Eingängen.

Die Bezeichnung „Differenzverstärker“ ist nicht zu verwechseln mit dem „Differenzierer“, der ebenfalls auf dieser Seite abgebildet ist. Der ebenfalls auf dieser Seite gezeigte „Instrumentenverstärker“ ist eine Abwandlung des Differenzverstärkers, der ebenfalls eine hohe Eingangsimpedanz aufweist.

Die gezeigte Schaltung berechnet die Differenz von zwei Spannungen, multipliziert mit einem Verstärkungsfaktor. Die Ausgangsspannung

V out = ( R f + R 1 ) R g ( R g + R 2 ) R 1 V 2 – R f R 1 V 1 = ( R 1 + R f R 1 ) ⋅ ( R g R g + R 2 ) V 2 – R f R 1 V 1 . {\displaystyle V_{\text{out}}={\frac {\left(R_{\text{f}}+R_{1}\right)R_{\text{g}}}{\left(R_{\text{g}}+R_{2}\right)R_{1}}}V_{2}-{\frac {R_{\text{f}}}{R_{1}}}V_{1}=\left({\frac {R_{1}+R_{\text{f}}}{R_{1}}}\right)\cdot \left({\frac {R_{\text{g}}}{R_{\text{g}}+R_{2}}}\right)V_{2}-{\frac {R_{\text{f}}}{R_{1}}}V_{1}.}

$V_{\text{out}}={\frac {\left(R_{\text{f}}+R_{1}\right)R_{\text{g}}}{\left(R_{\text{g}}+R_{2}\right)R_{1}}}V_{2}-{\frac {R_{\text{f}}}{R_{1}}}V_{1}=\left({\frac {R_{1}+R_{\text{f}}}{R_{1}}}\right)\cdot \left({\frac {R_{\text{g}}}{R_{\text{g}}+R_{2}}}\right)V_{2}-{\frac {R_{\text{f}}}{R_{1}}}V_{1}.$

Oder, ausgedrückt als Funktion des Gleichtakteingangs Vcom und des Differenzeingangs Vdif:

V com = ( V 1 + V 2 ) / 2 ; V dif = V 2 – V 1 , {\displaystyle V_{\text{com}}=(V_{1}+V_{2})/2;V_{\text{dif}}=V_{2}-V_{1},}

$V_{\text{com}}=(V_{1}+V_{2})/2;V_{\text{dif}}=V_{2}-V_{1},$

die Ausgangsspannung ist

V out R 1 R f = V com R 1 / R f – R 2 / R g 1 + R 2 / R g + V dif 1 + ( R 2 / R g + R 1 / R f ) / 2 1 + R 2 / R g . {\displaystyle V_{\text{out}}{\frac {R_{1}}{R_{\text{f}}}}=V_{\text{com}}{\frac {R_{1}/R_{\text{f}}-R_{2}/R_{\text{g}}}{1+R_{2}/R_{\text{g}}}}+V_{\text{dif}}{\frac {1+(R_{2}/R_{\text{g}}+R_{1}/R_{\text{f}})/2}{1+R_{2}/R_{\text{g}}}}.}

$V_{\text{out}}{\frac {R_{1}}{R_{\text{f}}}}=V_{\text{com}}{\frac {R_{1}/R_{\text{f}}-R_{2}/R_{\text{g}}}{1+R_{2}/R_{\text{g}}}}+V_{\text{dif}}{\frac {1+(R_{2}/R_{\text{g}}+R_{1}/R_{\text{f}})/2}{1+R_{2}/R_{\text{g}}}}.$

Damit diese Schaltung ein zur Spannungsdifferenz der Eingangsklemmen proportionales Signal erzeugt, muss der Koeffizient des Vcom-Terms (die Gleichtaktverstärkung) gleich Null sein, oder

R 1 / R f = R 2 / R g. {\displaystyle R_{1}/R_{\text{f}}=R_{2}/R_{\text{g}}.}

$R_{1}/R_{\text{f}}=R_{2}/R_{\text{g}}.$

Mit dieser Randbedingung ist das Gleichtaktunterdrückungsverhältnis dieser Schaltung unendlich groß, und der Ausgang

V out = R f R 1 V dif = R f R 1 ( V 2 – V 1 ) , {\displaystyle V_{\text{out}}={\frac {R_{\text{f}}}{R_{1}}}V_{\text{dif}}={\frac {R_{\text{f}}}{R_{1}}}\left(V_{2}-V_{1}\right),}

$V_{\text{out}}={\frac {R_{\text{f}}}{R_{1}}}V_{\text{dif}}={\frac {R_{\text{f}}}{R_{1}}}\left(V_{2}-V_{1}\right),$

wobei der einfache Ausdruck Rf / R1 die Regelverstärkung des Differenzverstärkers darstellt.

Der Spezialfall, bei dem die Regelverstärkung eins ist, ist ein Differenzialfolger, mit

V out = V 2 – V 1 . {\displaystyle V_{\text{out}}=V_{2}-V_{1}.}

$V_{\text{out}}=V_{2}-V_{1}.$

Invertierender VerstärkerEdit

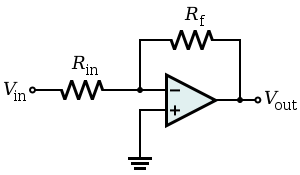
Ein invertierender Verstärker ist ein Spezialfall des Differenzverstärkers, bei dem der nichtinvertierende Eingang V2 dieser Schaltung geerdet ist und der invertierende Eingang V1 mit dem obigen Vin identifiziert wird. Die Regelverstärkung ist Rf / Rin, also

V out = – R f R in V in {\displaystyle V_{\text{out}}=-{\frac {R_{\text{f}}}{R_{\text{in}}}}V_{\text{in}}\!\,}

$V_{{{\text{out}}}}=-{\frac {R_{{{\text{f}}}}}{R_{{{\text{in}}}}}}V_{{{\text{in}}}}\!\,$

Die obige vereinfachte Schaltung ist wie der Differenzverstärker in der Grenze von R2 und Rg sehr klein. In diesem Fall ist die Schaltung jedoch aufgrund der Fehlanpassung zwischen Rf und Rin anfällig für eine Drift des Eingangsvorspannungsstroms.

Um die obige Verstärkungsgleichung intuitiv zu verstehen, berechnen Sie den Strom in Rin:

i in = V in R in {\displaystyle i_{\text{in}}={\frac {V_{\text{in}}{R_{\text{in}}}}}

$i_{{\text{in}}}}={\frac {V_{{\text{in}}}}}{R_{{\text{in}}}}}}$

Dann erinnern Sie sich, dass derselbe Strom durch Rf fließen muss, also (weil V- = V+ = 0):

V out = – i in R f = – V in R f R in {\displaystyle V_{\text{out}}=-i_{\text{in}}R_{\text{f}}=-V_{\text{in}}{\frac {R_{\text{f}}}{R_{\text{in}}}}}

$V_{\text{out}} = -i_{\text{in}} , R_{\text{f}} = - V_{\text{in}} \frac{ R_{\text{f}} }{ R_{\text{in}} }$

Eine mechanische Analogie ist eine Wippe, mit dem V-Knoten (zwischen Rin und Rf) als Drehpunkt, auf Erdpotential. Vin befindet sich in einer Länge Rin vom Drehpunkt entfernt; Vout befindet sich in einer Länge Rf. Wenn Vin „unter Masse“ sinkt, steigt der Ausgang Vout proportional an, um die Wippe auszugleichen, und umgekehrt.

Da der negative Eingang des Operationsverstärkers als virtuelle Masse wirkt, ist die Eingangsimpedanz dieser Schaltung gleich Rin.

Nicht-invertierender VerstärkerBearbeiten

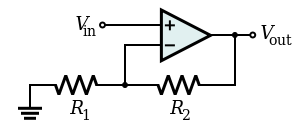
Ein nichtinvertierender Verstärker ist ein Spezialfall des Differenzverstärkers, bei dem der invertierende Eingang V1 dieser Schaltung geerdet ist und der nichtinvertierende Eingang V2 mit dem obigen Vin identifiziert wird, mit R1 ≫ R2.Bezogen auf die Schaltung unmittelbar oben,

V out = ( 1 + R 2 R 1 ) V in {\displaystyle V_{\text{out}}=\left(1+{\frac {R_{\text{2}}}{R_{\text{1}}}}\right)V_{\text{in}}\!\,}

$V_{{{\text{out}}}}=\left(1+{\frac {R_{{{\text{2}}}}}{R_{{{\text{1}}}}}}\right)V_{{{\text{in}}}}\!\,$

Um diese Verstärkungsgleichung intuitiv zu verstehen, verwenden Sie die Technik der virtuellen Masse, um den Strom im Widerstand R1 zu berechnen:

i 1 = V in R 1 , {\displaystyle i_{1}={\frac {V_{\text{in}}{R_{1}}},,}

$i_{1}={\frac {V_{{{\text{in}}}}}{R_{1}}}},,$

Erinnern Sie sich dann daran, dass derselbe Strom durch R2 fließen muss, also:

V out = V in + i 1 R 2 = V in ( 1 + R 2 R 1 ) {\displaystyle V_{\text{out}}=V_{\text{in}}+i_{1}R_{2}=V_{\text{in}}\left(1+{\frac {R_{2}}{R_{1}}}\right)}

$V_{\text{out}}=V_{\text{in}}+i_{1}R_{2}=V_{\text{in}}\left(1+{\frac {R_{2}}{R_{1}}}\right)$

Im Gegensatz zum invertierenden Verstärker, kann ein nicht-invertierender Verstärker keine Verstärkung von weniger als 1 haben.

Eine mechanische Analogie ist ein Klasse-2-Hebel, mit einem Anschluss von R1 als Drehpunkt, der auf Massepotential liegt. Vin befindet sich in einer Länge R1 vom Drehpunkt entfernt, Vout in einer Länge R2 weiter. Wenn Vin „über Masse“ steigt, steigt der Ausgang Vout proportional mit dem Hebel.

Die Eingangsimpedanz des vereinfachten nicht-invertierenden Verstärkers ist hoch:

Z in = ( 1 + A OL B ) Z dif {\displaystyle Z_{\text{in}}=(1+A_{\text{OL}}B)Z_{\text{dif}}

$Z_{\text{in}}=(1+A_{\text{OL}}B)Z_{\text{dif}}$

wobei Zdif die Eingangsimpedanz des Operationsverstärkers für Differenzsignale ist, und AOL die Open-Loop-Spannungsverstärkung des Operationsverstärkers ist (die mit der Frequenz variiert), und B der Rückkopplungsfaktor ist (der Anteil des Ausgangssignals, der zum Eingang zurückkehrt). Im Fall des idealen Operationsverstärkers, bei dem AOL unendlich und Zdif unendlich ist, ist auch die Eingangsimpedanz unendlich. In diesem Fall ist die Schaltung jedoch aufgrund der Fehlanpassung zwischen den Impedanzen, die die V+- und V–Operationsverstärkereingänge antreiben, anfällig für eine Drift des Eingangsvorspannungsstroms.

Die Rückkopplungsschleife verringert die Ausgangsimpedanz auf ähnliche Weise:

Z out = Z OL 1 + A OL B {\displaystyle Z_{\text{out}}={\frac {Z_{\text{OL}}{1+A_{\text{OL}}B}}}

$Z_{\text{out}}={\frac {Z_{\text{OL}}{1+A_{\text{OL}}B}}$

wobei Zout die Ausgangsimpedanz mit Rückkopplung und ZOL die Ausgangsimpedanz mit offener Schleife ist.

Spannungsfolger (Einheits-Pufferverstärker)

Wird als Pufferverstärker verwendet, um Ladeeffekte zu eliminieren (z.B., Anschluss eines Geräts mit hoher Quellimpedanz an ein Gerät mit niedriger Eingangsimpedanz).

V out = V in {\displaystyle V_{\text{out}}=V_{\text{in}}\!}

$V_{\text{out}}=V_{\text{in}}\!$

Z in = ∞ {\displaystyle Z_{\text{in}}=\infty }

$Z_{{\text{in}}}}=\infty$

(realistisch gesehen die differentielle Eingangsimpedanz des Operationsverstärkers selbst (1 MΩ bis 1 TΩ), multipliziert mit der Open-Loop-Verstärkung des Operationsverstärkers)

Aufgrund der starken (d. h. Einheitsverstärkung) Rückkopplung und bestimmter nicht idealer Eigenschaften realer Operationsverstärker neigt dieses Rückkopplungssystem dazu, schlechte Stabilitätsmargen zu haben. Folglich kann das System instabil sein, wenn es an ausreichend kapazitive Lasten angeschlossen wird. In diesen Fällen kann ein Verzögerungskompensationsnetzwerk (z. B. Verbindung der Last mit dem Spannungsfolger über einen Widerstand) verwendet werden, um die Stabilität wiederherzustellen. Das Herstellerdatenblatt für den Operationsverstärker kann eine Anleitung für die Auswahl der Komponenten in externen Kompensationsnetzwerken bieten. Alternativ kann ein anderer Operationsverstärker gewählt werden, der über eine geeignetere interne Kompensation verfügt.

Die Eingangs- und Ausgangsimpedanz werden von der Rückkopplungsschleife auf die gleiche Weise beeinflusst wie beim nicht-invertierenden Verstärker mit B=1.

SummenverstärkerBearbeiten

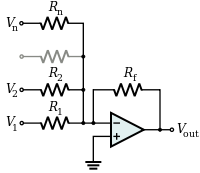
Ein Summierverstärker summiert mehrere (gewichtete) Spannungen:

V out = – R f ( V 1 R 1 + V 2 R 2 + ⋯ + V n R n ) {\displaystyle V_{\text{out}}=-R_{\text{f}}\left({\frac {V_{1}}{R_{1}}}+{\frac {V_{2}}{R_{2}}+\cdots +{\frac {V_{n}}{R_{n}}\right)}

$V_{{\text{out}}}}=-R_{{\text{f}}}}\left({\frac {V_{1}}{R_{1}}}+{\frac {V_{2}}{R_{2}}}+\cdots +{\frac {V_{n}}{R_{n}}\right)$

Wenn R 1 = R 2 = ⋯ = R n {\displaystyle R_{1}=R_{2}=\cdots =R_{n}}
$R_{1}=R_{2}=\cdots =R_{n}$

, und R f {\displaystyle R_{\text{f}}}

$R_{{{\text{f}}}}$

unabhängig

V out = – R f R 1 ( V 1 + V 2 + ⋯ + V n ) {\displaystyle V_{\text{out}}=-{\frac {R_{\text{f}}}{R_{1}}}(V_{1}+V_{2}+\cdots +V_{n})\!}

$V_{\text{out}}=-{\frac {R_{\text{f}}}{R_{1}}(V_{1}+V_{2}+\cdots +V_{n})\!$

Wenn R 1 = R 2 = ⋯ = R n = R f {\displaystyle R_{1}=R_{2}=\cdots =R_{n}=R_{\text{f}}}
$R_{1}=R_{2}=\cdots =R_{n}=R_{{\text{f}}}}$

V out = – ( V 1 + V 2 + ⋯ + V n ) {\displaystyle V_{\text{out}}=-(V_{1}+V_{2}+\cdots +V_{n})\!}

$V_{\text{out}}=-(V_{1}+V_{2}+\cdots +V_{n})\!$

Ausgang ist invertiert
Eingangsimpedanz des n-ten Eingangs ist Z n = R n {\displaystyle Z_{n}=R_{n}}
$Z_{n}=R_{n}$

( V – {\displaystyle V_{-}}

$V_{-}$

ist eine virtuelle Masse)