Backpropagation Schritt für Schritt

Wenn Sie Ihr eigenes neuronales Netzwerk aufbauen, müssen Sie auf jeden Fall verstehen, wie man es trainiert.

Backpropagation ist eine häufig verwendete Technik zum Trainieren von neuronalen Netzwerken. Es gibt viele Ressourcen, die die Technik erklären, aber dieser Beitrag wird Backpropagation mit einem konkreten Beispiel in sehr detaillierten, bunten Schritten erklären.

Sie können die Visualisierung des Vorwärtsdurchlaufs und der Backpropagation hier sehen. Sie können Ihr neuronales Netzwerk mit netflow bauen.js

Übersicht

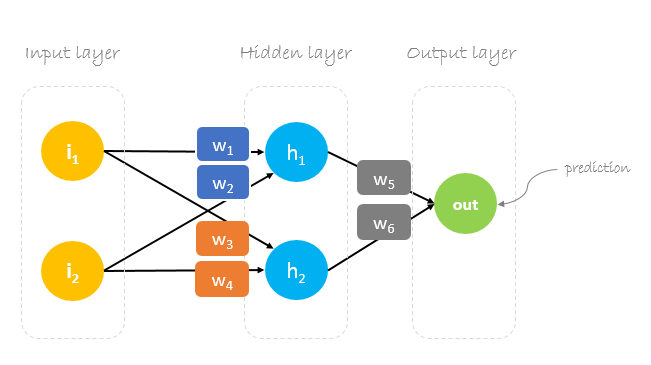
In diesem Beitrag werden wir ein neuronales Netzwerk mit drei Schichten aufbauen:

• Eingabeschicht mit zwei Eingangsneuronen
• Eine versteckte Schicht mit zwei Neuronen
• Ausgabeschicht mit einem einzelnen Neuron

Gewichte, Gewichte, Gewichte

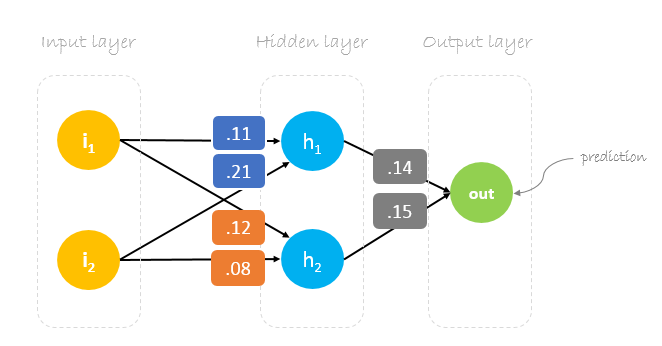
Beim Training eines neuronalen Netzes geht es darum, Gewichte zu finden, die den Vorhersagefehler minimieren. Normalerweise beginnen wir unser Training mit einem Satz zufällig generierter Gewichte, die dann mittels Backpropagation aktualisiert werden, um beliebige Eingaben korrekt auf Ausgaben abzubilden.

Unsere anfänglichen Gewichte werden wie folgt aussehen:w1 = 0.11w2 = 0.21w3 = 0.12w4 = 0.08w5 = 0.14 und w6 = 0.15

Datensatz

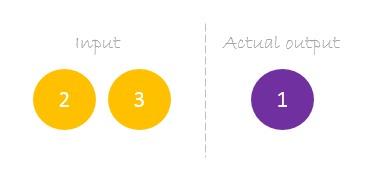
Unser Datensatz hat eine Probe mit zwei Eingängen und einem Ausgang.

Unser einzelnes Beispiel sieht wie folgt aus: inputs= und output=.

Vorwärtspass

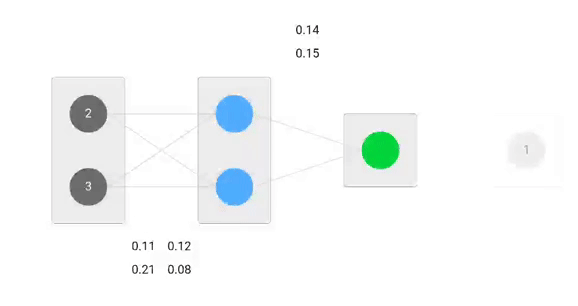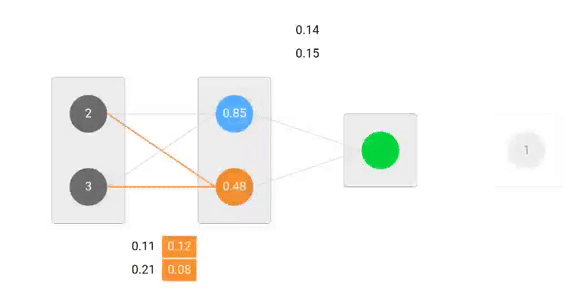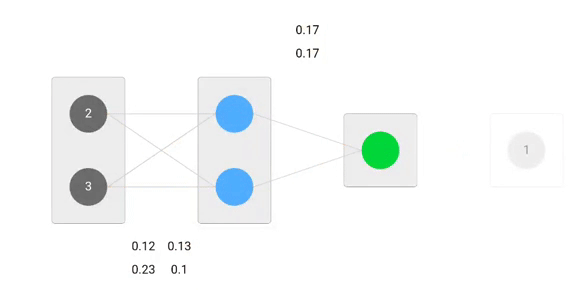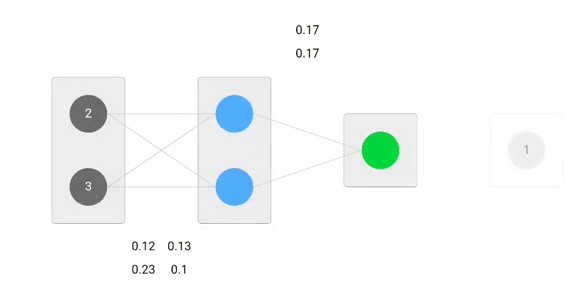
Wir verwenden gegebene Gewichte und Eingaben, um die Ausgabe vorherzusagen. Die Eingaben werden mit den Gewichten multipliziert; die Ergebnisse werden dann an die nächste Schicht weitergegeben.

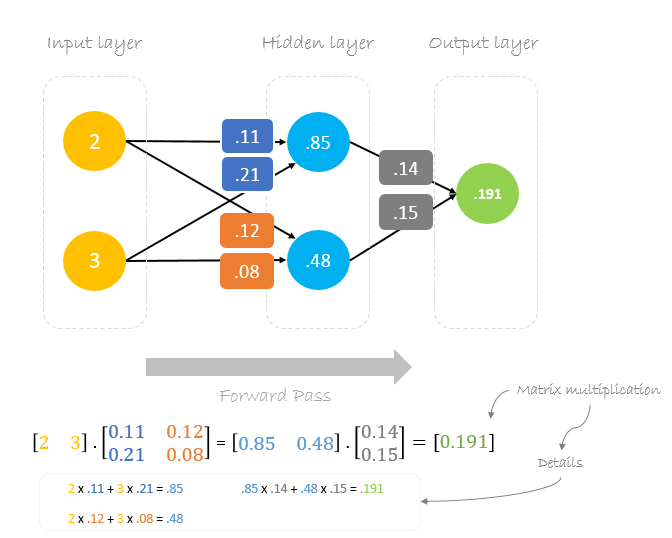
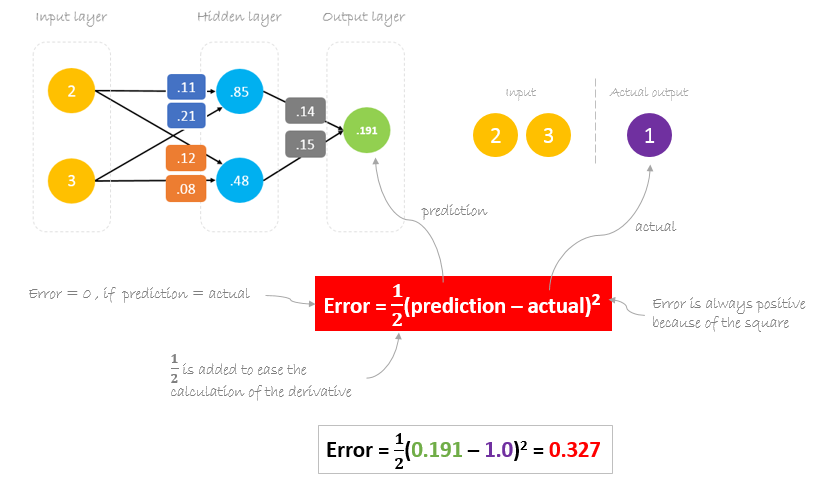
Fehlerberechnung

Nun ist es an der Zeit, herauszufinden, wie unser Netzwerk abgeschnitten hat, indem wir die Differenz zwischen der tatsächlichen und der vorhergesagten Ausgabe berechnen. Es ist klar, dass unsere Netzwerkausgabe oder Vorhersage nicht einmal annähernd der tatsächlichen Ausgabe entspricht. Wir können die Differenz oder den Fehler wie folgt berechnen.

Fehler reduzieren

Unser Hauptziel des Trainings ist es, den Fehler oder die Differenz zwischen Vorhersage und tatsächlicher Ausgabe zu reduzieren. Da die tatsächliche Ausgabe konstant ist, sich also nicht ändert, besteht die einzige Möglichkeit, den Fehler zu reduzieren, darin, den Vorhersagewert zu ändern. Die Frage ist nun, wie man den Vorhersagewert ändern kann?

Bei der Zerlegung der Vorhersage in ihre Grundelemente können wir feststellen, dass die Gewichte die variablen Elemente sind, die den Vorhersagewert beeinflussen. Mit anderen Worten, um den Vorhersagewert zu ändern, müssen wir die Gewichtungswerte ändern.

Die Frage ist nun, wie man die Gewichtungswerte ändern kann, damit der Fehler reduziert wird?
Die Antwort ist Backpropagation!

Backpropagation

Backpropagation, kurz für „Rückwärtsfortpflanzung von Fehlern“, ist ein Mechanismus, der verwendet wird, um die Gewichte mittels Gradientenabstieg zu aktualisieren. Dabei wird der Gradient der Fehlerfunktion in Bezug auf die Gewichte des neuronalen Netzes berechnet. Die Berechnung erfolgt rückwärts durch das Netz.

Gradientenabstieg ist ein iterativer Optimierungsalgorithmus zum Finden des Minimums einer Funktion; in unserem Fall wollen wir die Fehlerfunktion minimieren. Um ein lokales Minimum einer Funktion mit Hilfe des Gradientenabstiegs zu finden, macht man Schritte, die proportional zum Negativ des Gradienten der Funktion am aktuellen Punkt sind.

Zum Beispiel, um w6 zu aktualisieren, nehmen wir das aktuelle w6 und subtrahieren die partielle Ableitung der Fehlerfunktion in Bezug auf w6. Optional multiplizieren wir die Ableitung der Fehlerfunktion mit einer ausgewählten Zahl, um sicherzustellen, dass das neue aktualisierte Gewicht die Fehlerfunktion minimiert; diese Zahl wird Lernrate genannt.

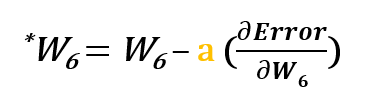
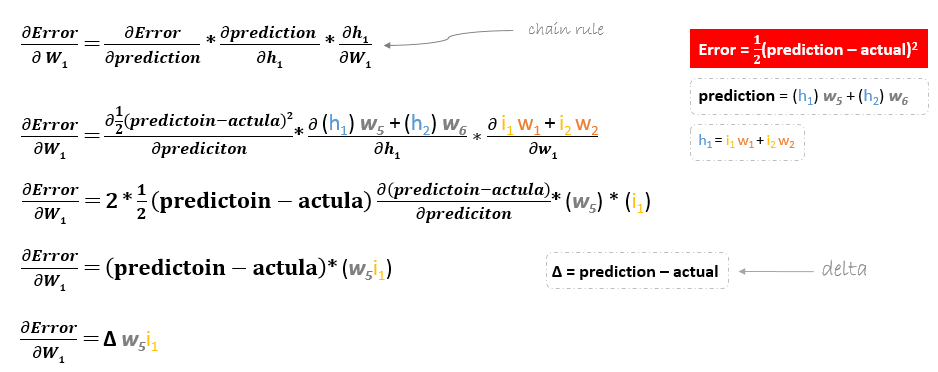
Die Ableitung der Fehlerfunktion wird durch Anwendung der Kettenregel wie folgt ausgewertet

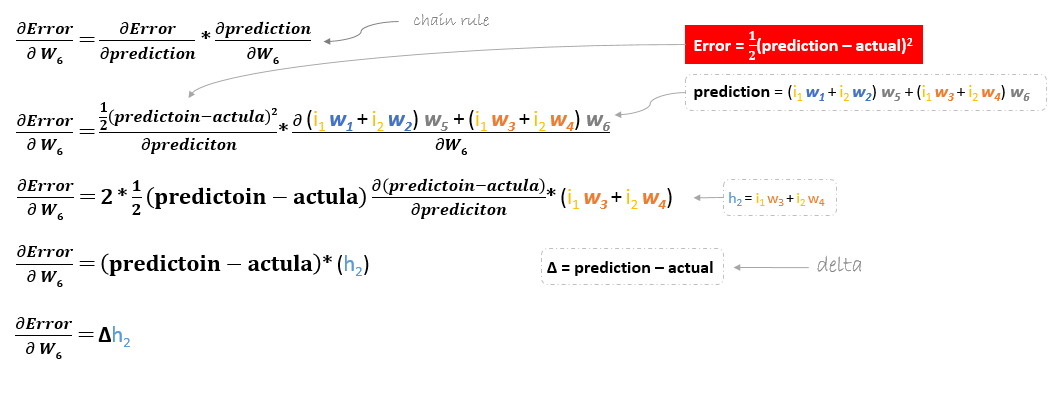
Um also w6 zu aktualisieren, können wir die folgende Formel anwenden

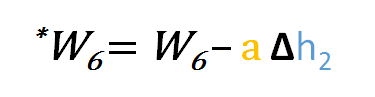
In ähnlicher Weise können wir die Aktualisierungsformel für w5 und alle anderen Gewichte, die zwischen der Ausgabe und der versteckten Schicht existieren, ableiten.

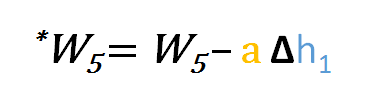
Wenn man sich jedoch rückwärts bewegt, um w1w2w3 und w4 zu aktualisieren, die zwischen Eingabe und versteckter Schicht existieren, sieht die partielle Ableitung für die Fehlerfunktion nach w1 zum Beispiel wie folgt aus.

Auf die gleiche Weise können wir die Aktualisierungsformel für die übrigen Gewichte w2w3 und w4 finden.

Zusammengefasst lauten die Aktualisierungsformeln für alle Gewichte wie folgt:

Wir können die Aktualisierungsformeln in Matrizen wie folgt umschreiben

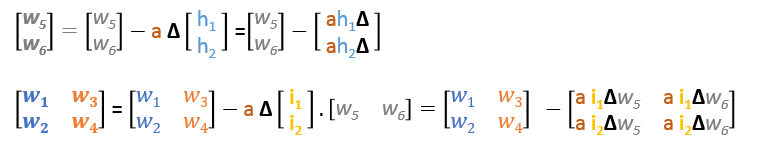
Rückwärtspass

Mit abgeleiteten Formeln können wir die neuen Gewichte finden.

Lernrate: ist ein Hyperparameter, was bedeutet, dass wir seinen Wert manuell schätzen müssen.

Nun, unter Verwendung der neuen Gewichte wiederholen wir den Vorwärtsdurchlauf

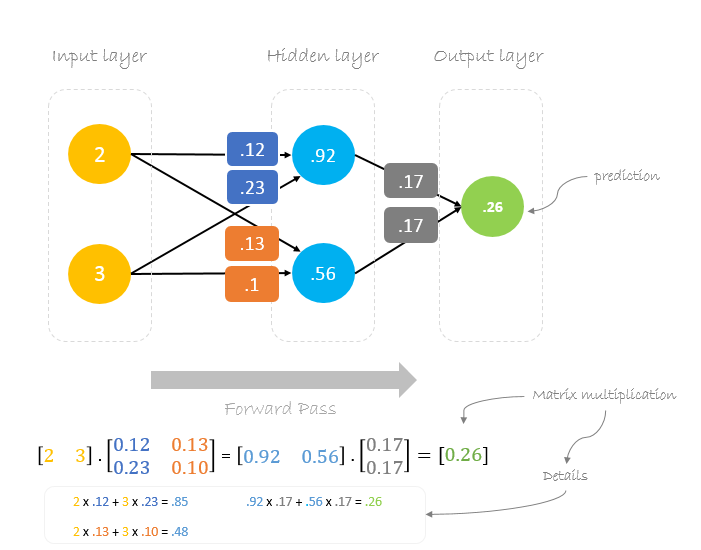
Wir können feststellen, dass die Vorhersage 0.26 etwas näher an der tatsächlichen Ausgabe liegt als die zuvor vorhergesagte 0.191. Wir können den gleichen Prozess des Rückwärts- und Vorwärtsdurchlaufs wiederholen, bis der Fehler nahe oder gleich Null ist.

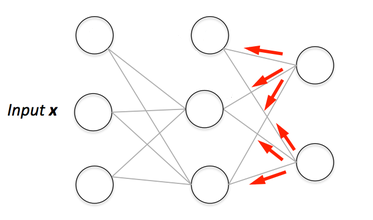
Visualisierung der Backpropagation

Sie können die Visualisierung des Vorwärtsdurchlaufs und der Backpropagation hier sehen.

Sie können Ihr neuronales Netzwerk mit netflow.js aufbauen