Chang Hsin Lee

Wenn ich ein maschinelles Lernmodell für Klassifikationsprobleme entwickle, ist eine der Fragen, die ich mir stelle, warum mein Modell nicht Mist ist. Manchmal habe ich das Gefühl, dass die Entwicklung eines Modells wie das Halten einer Granate ist, und die Kalibrierung ist eine meiner Sicherheitsnadeln. In diesem Beitrag werde ich das Konzept der Kalibrierung durchgehen und dann in Python zeigen, wie man diagnostische Kalibrierungsplots erstellt.

Hier ist der Link zum Jupyter-Notebook für diesen Beitrag

Evaluieren probabilistischer Vorhersagen

Lassen Sie mich zunächst erklären, was Kalibrierung ist und woher die Idee stammt.

Beim maschinellen Lernen erzeugen die meisten Klassifikationsmodelle Vorhersagen von Klassenwahrscheinlichkeiten zwischen 0 und 1 und haben dann die Möglichkeit, probabilistische Ausgaben in Klassenvorhersagen umzuwandeln. Selbst Algorithmen, die nur Scores erzeugen, wie z. B. Support Vector Machine, können so nachgerüstet werden, dass sie wahrscheinlichkeitsähnliche Vorhersagen erzeugen.

Für ein binäres Klassifikationsproblem gibt es zusammenfassende Metriken – Genauigkeit, Präzision, Recall, F1-Score usw. -, die die Qualität von binären 0- und 1-Ausgaben bewerten. Wenn die Ausgaben nicht binär sind, sondern Fließkommazahlen zwischen 0 und 1 sind, kann ich sie als Scores für die Klassifizierung verwenden. Aber fließende Zahlen zwischen 0 und 1 schreien nach Wahrscheinlichkeiten, und woher weiß ich, ob ich ihnen als Wahrscheinlichkeiten trauen kann?

Die Ausgabe eines Modells kann als eine Aussage darüber betrachtet werden, wie wahrscheinlich es ist, dass etwas passiert. Ein Beispiel für ein solches Modell – dessen Aussagen ich jeden Tag prüfe, bevor ich mein Haus verlasse – ist der Wetterdienst. Insbesondere, wie wahrscheinlich ist es, dass es regnet?

Bild von weather.com

Es sagt, dass es am Sonntag eine 80%ige Chance auf Regen gibt. Wie vertrauenswürdig ist diese 80%-Ansage? Wenn ich mir die vergangenen Vorhersagen von weather.com ansehe und herausfinde, dass 8 von 10 Tagen regnerisch sind, wenn sie eine 80%ige Vorhersage gemacht haben, dann kann ich mich selbst davon überzeugen, meine Hörbücher zu laden und mich auf einen verrückten Verkehr auf der Autobahn am Nachmittag vorzubereiten.

In anderen Worten, eine genaue Wettervorhersage bedeutet, dass wenn ich mir 100 Tage ansehe, die mit einer 80%igen Regenwahrscheinlichkeit vorhergesagt sind, dann sollte es ungefähr 80 Regentage geben. Sie muss auch in anderen Wahrscheinlichkeitsbereichen genau sein. Für Tage, für die eine Regenwahrscheinlichkeit von 30 % vorhergesagt wird, sollte es im Durchschnitt 30 Regentage von 100 Tagen geben. Wenn die Vorhersagen dieses Wettervorhersagedienstes alle diesem guten Muster folgen, dann sagen wir, dass ihre Vorhersagen kalibriert sind. Das ist die probabilistische Art zu sagen, dass sie den Nagel auf den Kopf getroffen haben.

• Ein probabilistisches Modell ist kalibriert, wenn ich die Teststichproben auf der Basis ihrer vorhergesagten Wahrscheinlichkeiten in Kisten eingeteilt habe und die wahren Ergebnisse jeder Kiste einen Anteil haben, der nahe an den Wahrscheinlichkeiten in der Kiste liegt.

Wie kann ich die Kalibrierung beurteilen? Anstatt die Kalibrierung in einer einzigen Zahl zusammenzufassen, ziehe ich es vor, Kalibrierungsplots zu erstellen.

Kalibrierungsplots sind oft Liniendiagramme. Sobald ich die Anzahl der Bins gewählt und Vorhersagen in die Bins geworfen habe, wird jedes Bin in einen Punkt auf dem Plot umgewandelt. Für jedes Bin ist der y-Wert der Anteil der wahren Ergebnisse, und der x-Wert ist die mittlere vorhergesagte Wahrscheinlichkeit. Daher hat ein gut kalibriertes Modell eine Kalibrierungskurve, die der geraden Linie y=x folgt. Hier ist ein Beispiel für ein Kalibrierungsdiagramm mit zwei Kurven, die jeweils ein Modell auf denselben Daten darstellen.

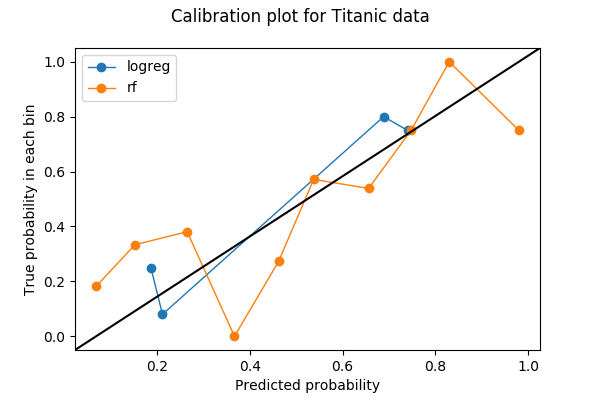
Ich werde zeigen, wie ich dieses Diagramm in Python erstellt habe und was ich darin gesehen habe.

Ein Python-Beispiel

Das erste, was man bei der Erstellung eines Kalibrierungsdiagramms tun muss, ist, die Anzahl der Bins zu wählen. In diesem Beispiel habe ich die Wahrscheinlichkeiten in 10 Bins zwischen 0 und 1 eingeteilt: von 0 bis 0,1, 0,1 bis 0,2, …, 0,9 bis 1. Die Daten, die ich verwendet habe, sind der Titanic-Datensatz von Kaggle, bei dem das vorherzusagende Label eine binäre Variable Survived ist.

Ich werde die Kalibrierungskurven für zwei Modelle darstellen – eines für logistische Regression und eines für Random Forest. Beide Modelle erzeugen Klassenwahrscheinlichkeiten auf Survived basierend auf zwei Features Age und Sex.

+----+------+--------+| Age| Sex|Survived|+----+------+--------+|22.0| male| 0||38.0|female| 1||26.0|female| 1|+----+------+--------+

Vorverarbeitung

Bevor ich meine Modelle trainierte, füllte ich die fehlenden Werte in Age mit ihrem Mittelwert auf und verwandelte außerdem Sex in eine numerische Variable mit den Werten 0 und 1.

import numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom sklearn import preprocessingfrom sklearn import model_selectiontitanic = pd.read_csv('train.csv')fitted_age_imputer = preprocessing.Imputer(axis=1).fit(titanic.values)titanic = fitted_age_imputer.transform( titanic.values.reshape(1, -1) ).transpose()titanic = np.where(titanic.Sex == 'female', 1, 0)

Dann habe ich die Daten durch eine 80/20-Aufteilung in Trainings- und Validierungsset aufgeteilt.

from sklearn import model_selectionfeature_cols = feature_train, feature_test, label_train, label_test = ( model_selection.train_test_split( titanic, titanic.Survived, test_size=0.2, random_state=1) )

Training und Vorhersage

Ich kann nun ein logistisches Regressionsmodell auf meiner Trainingsmenge trainieren und auf der Validierungsmenge vorhersagen.

from sklearn.linear_model import LogisticRegressionlogreg_model = LogisticRegression().fit(X=feature_train,y=label_train)logreg_prediction = logreg_model.predict_proba(feature_test)

In ähnlicher Weise kann ich ein Random-Forest-Modell trainieren und auf dem Validierungsset vorhersagen.

from sklearn.ensemble import RandomForestClassifierrf_model = RandomForestClassifier(random_state=1234).fit(X=feature_train, y=label_train)rf_prediction = rf_model.predict_proba(feature_test)

Die positive Klassenwahrscheinlichkeit wird von den Modellen in der zweiten Spalte (Index=1) geliefert:

logreg_prediction

array(, , , , ])

Kalibrierungsplot

Sobald ich die Klassenwahrscheinlichkeiten und Bezeichnungen habe, kann ich die Bins für einen Kalibrierungsplot berechnen. Hier verwende ich sklearn.calibration.calibration_curve, das die (x,y) Koordinaten der Bins auf dem Kalibrierungsdiagramm zurückgibt.

from sklearn.calibration import calibration_curvelogreg_y, logreg_x = calibration_curve(label_test, logreg_prediction, n_bins=10)

Beachten Sie, dass, obwohl ich nach 10 Bins für die logistische Regression gefragt habe, 6 von 10 Bins keine Daten haben. Der Grund dafür ist eine Kombination aus der Tatsache, dass die logistische Regression ein einfaches Modell ist, dass es nur zwei Features gibt und dass ich weniger als 200 Datenpunkte im Validierungsset habe.

), array()]

Als Nächstes berechne ich die Koordinaten für die Bins des Random Forest-Modells.

rf_y, rf_x = calibration_curve(label_test, rf_prediction, n_bins=10)

Nun kann ich die beiden Kalibrierungskurven darstellen. Um den Plot besser lesbar zu machen, habe ich außerdem eine y=x-Referenzlinie hinzugefügt, die auf einer StackOverflow-Antwort basiert.

%matplotlib inlineimport matplotlib.pyplot as pltimport matplotlib.lines as mlinesimport matplotlib.transforms as mtransformsfig, ax = plt.subplots()# only these two lines are calibration curvesplt.plot(logreg_x,logreg_y, marker='o', linewidth=1, label='logreg')plt.plot(rf_x, rf_y, marker='o', linewidth=1, label='rf')# reference line, legends, and axis labelsline = mlines.Line2D(, , color='black')transform = ax.transAxesline.set_transform(transform)ax.add_line(line)fig.suptitle('Calibration plot for Titanic data')ax.set_xlabel('Predicted probability')ax.set_ylabel('True probability in each bin')plt.legend()plt.show()

Bin-Summen und Diskriminierung

Es gibt nur 4 nicht leere Bins für die logistische Regression, obwohl ich um 10 Bins gebeten habe. Ist das ein schlechtes Ergebnis? Lassen Sie uns eine Funktion verwenden, die ich aus dem Quellcode von sklearn.calibration.calibration_curve entnommen habe, um herauszufinden, welches die fehlenden Bins sind.

def bin_total(y_true, y_prob, n_bins): bins = np.linspace(0., 1. + 1e-8, n_bins + 1) # In sklearn.calibration.calibration_curve, # the last value in the array is always 0. binids = np.digitize(y_prob, bins) - 1 return np.bincount(binids, minlength=len(bins))bin_total(label_test, logreg_prediction, n_bins=10)

array(, dtype=int64)

Die fehlenden Bins haben Mittelwerte von 5%, 35%, 45%, 55%, 85% und 95%. Tatsächlich können niedrige Summen oder leere Bins in den mittleren Bins (30-60%) sogar eine gute Sache sein – ich möchte, dass meine Vorhersagen diese mittleren Bins vermeiden und diskriminativ werden.

Diskriminierung ist ein Konzept, das bei Klassifikationsproblemen Seite an Seite mit der Kalibrierung geht. Manchmal kommt es vor der Kalibrierung, wenn das Ziel bei der Erstellung eines Modells darin besteht, automatische Entscheidungen zu treffen, anstatt statistische Schätzungen zu liefern. Stellen Sie sich ein Szenario vor, in dem ich zwei Wettermodelle habe und in Podunk, Nevada, lebe, wo 10 % (36 Tage pro Jahr) der Tage regnerisch sind:

• Modell A sagt immer, dass es 10 % Regenwahrscheinlichkeit gibt, egal welcher Tag es ist.
• Modell B sagt, dass es im Juni jeden Tag regnen wird (100 %), und in den anderen 11 Monaten nie regnet (0 %).

Modell A ist perfekt kalibriert. Es gibt nur einen Bereich – den 10 %-Bereich – und die wahre Wahrscheinlichkeit beträgt 10 %. Modell B hingegen ist etwas falsch kalibriert, da es 30 Tage im 100%-Bin gibt, aber auch 6 Regentage im 0%-Bin. Aber Modell B ist eindeutig nützlicher, wenn ich Wochenend-Wanderpläne mache. Modell B ist diskriminanter als A, weil es einfacher ist, Entscheidungen (wandern/nicht wandern) basierend auf den Ergebnissen von Modell B zu treffen.

Die Diskriminierung wird oft mit den Receiver-Operating-Characteristic-Kurven (ROC-Kurven) überprüft, aber das ist ein Thema für einen anderen Beitrag.

Cross-Validierung?

Wenn ich mich nicht um die Diskriminierung kümmere und nur eine gute Kalibrierung möchte, dann scheint die logistische Regression (blau) besser abzuschneiden als Random Forest (orange). Ist das wirklich der Fall? Insbesondere, wenn ich mir die Anzahl der Punkte in den Bins für Random Forest ansehe,

bin_total(label_test, rf_prediction, n_bins=10)

array(, dtype=int64)

Ich vermute, dass das Problem darin liegen könnte, dass einige Bins zu wenige Datenpunkte haben. Ich habe 200 Punkte in 10 Bins gelegt, also werden einige Bins nur wenige bekommen, daher leidet der Kalibrierungsplot, weil eine Fehlklassifikation in einem winzigen Bin das Verhältnis stark verändert.

Nur 20% meiner Daten wurden im vorherigen Plot verwendet, also kann ich vielleicht mehr verwenden. Um alle meine Daten beim Testen der Kalibrierung zwischen verschiedenen Modellen zu verwenden, dachte ich, ich könnte die Idee der Kreuzvalidierung stehlen. Wenn ich meine Daten für die Kreuzvalidierung in 5 Foldings aufteile, wird jeder Fold einmal als Validierungsset verwendet. Daher kann ich die vorhergesagten Wahrscheinlichkeiten aus allen 5 Falten verketten und daraus ein Kalibrierungsdiagramm erstellen. Das Ergebnis einer 5-fachen Kalibrierungsdarstellung ist die folgende Darstellung. Der Code ist im letzten Abschnitt des Jupyter-Notebooks zu finden.

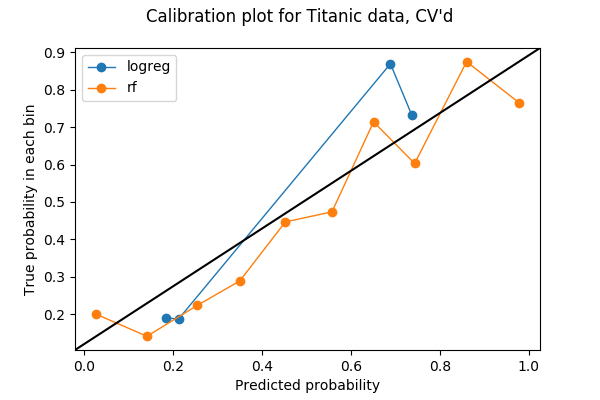
Jedes Bin hat nun mehr Punkte:

array(, dtype=int64)

und ich denke, man kann mit Sicherheit sagen, dass in diesem Beispiel der Random Forest besser kalibriert ist als die logistische Regression.

***

Nate Silver hat ein großartiges Beispiel zur Wetterkalibrierung in dem Buch The Signal and the Noise, wo er in Kapitel 4, For Years You’ve Been Telling Us That Rain Is Green, die Vorhersagen von drei Quellen – dem National Weather Service, dem Weather Channel und lokalen Nachrichtensendern – untersucht. Er kam zu dem Schluss, dass die meisten lokalen Nachrichtensender schlecht kalibriert sind und „nass“ sind. Es ist ein Juwel, und ich empfehle, das Buch in die Hand zu nehmen, wenn Sie es in die Finger bekommen.

Ich habe zum ersten Mal durch meinen Kollegen Kevin im Jahr 2016 über Kalibrierung gelernt, als wir verschiedene Metriken zu Klassifikationsmodellen diskutierten. Ohne ihn wird es wahrscheinlich noch ein oder zwei Jahre dauern, bis ich die Bedeutung der Kalibrierung erkenne, und viel später, bevor ich diesen Beitrag schreibe.