College Algebra
Lernergebnisse
- Umrechnung von logarithmischer in exponentielle Form.
- Umrechnung von exponentieller in logarithmische Form.
Um die Stärke von Erdbeben zu analysieren oder die Stärke von zwei verschiedenen Erdbeben zu vergleichen, müssen wir in der Lage sein, zwischen logarithmischer und exponentieller Form umzurechnen. Nehmen wir zum Beispiel an, dass die Energiemenge, die von einem Erdbeben freigesetzt wurde, 500-mal größer war als die Energiemenge, die von einem anderen freigesetzt wurde. Wir wollen den Unterschied in der Magnitude berechnen. Die Gleichung, die dieses Problem darstellt, lautet {10}^{x}=500, wobei x die Differenz der Magnituden auf der Richterskala darstellt. Wie würden wir für x lösen?
Wir haben noch keine Methode zum algebraischen Lösen von Exponentialgleichungen gelernt. Keines der bisher besprochenen algebraischen Hilfsmittel ist ausreichend, um {10}^{x}=500 zu lösen. Wir wissen, dass {10}^{2}=100 und {10}^{3}=1000 ist, also ist es klar, dass x irgendein Wert zwischen 2 und 3 sein muss, da y={10}^{x} steigend ist. Wir können einen Graphen untersuchen, um die Lösung besser abzuschätzen.
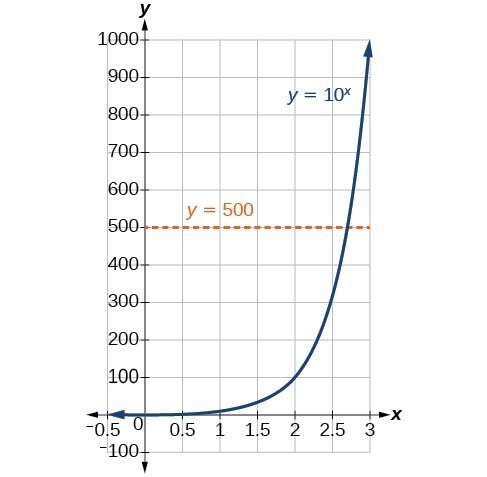
Das Abschätzen anhand eines Graphen ist jedoch ungenau. Um eine algebraische Lösung zu finden, müssen wir eine neue Funktion einführen. Beachten Sie, dass der obige Graph den Test der horizontalen Linie besteht. Die Exponentialfunktion y={b}^{x} ist eineindeutig, also ist ihre Inverse, x={b}^{y}, auch eine Funktion. Wie bei allen inversen Funktionen tauschen wir einfach x und y aus und lösen nach y, um die inverse Funktion zu finden. Um y als Funktion von x darzustellen, verwenden wir eine logarithmische Funktion der Form y={\mathrm{log}}_{b}\left(x\right). Der Logarithmus zur Basis b einer Zahl ist der Exponent, um den wir b erhöhen müssen, um diese Zahl zu erhalten.
Wir lesen einen logarithmischen Ausdruck als: „Der Logarithmus zur Basis b von x ist gleich y“, oder, vereinfacht gesagt, „log zur Basis b von x ist y.“ Wir können auch sagen: „b hoch y ist x“, denn Logarithmen sind Exponenten. Zum Beispiel ist der Logarithmus zur Basis 2 von 32 gleich 5, weil 5 der Exponent ist, den wir auf 2 anwenden müssen, um 32 zu erhalten. Da {2}^{5}=32 ist, können wir schreiben: {\mathrm{log}}_{2}32=5. Wir lesen dies als „log Basis 2 von 32 ist 5.“
Wir können die Beziehung zwischen der logarithmischen Form und der entsprechenden Exponentialform wie folgt ausdrücken:
{\mathrm{log}}_{b}\left(x\right)=y\Leftrightarrow {b}^{y}=x,\text{}b>0,b\ne 1
Beachte, dass die Basis b immer positiv ist.
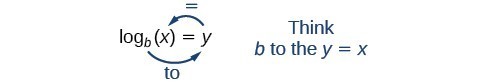
Da ein Logarithmus eine Funktion ist, wird er am korrektesten als {\mathrm{log}}_{b}\left(x\right) geschrieben, wobei Klammern verwendet werden, um die Funktionsauswertung zu bezeichnen, genauso wie wir es mit f\left(x\right) tun würden. Wenn die Eingabe jedoch eine einzelne Variable oder Zahl ist, werden die Klammern häufig weggelassen und der Ausdruck ohne Klammern als {\mathrm{log}}_{b}x geschrieben. Beachten Sie, dass viele Taschenrechner Klammern um das x benötigen.
Wir können die Notation von Logarithmen wie folgt veranschaulichen:
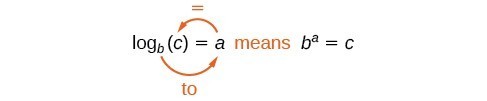
Beachten Sie, dass beim Vergleich der Logarithmusfunktion und der Exponentialfunktion der Eingang und der Ausgang vertauscht werden. Das bedeutet, dass y={\mathrm{log}}_{b}\left(x\right) und y={b}^{x} inverse Funktionen sind.
Ein allgemeiner Hinweis: Definition der logarithmischen Funktion
Ein Logarithmus zur Basis b einer positiven Zahl x erfüllt die folgende Definition:
Für x>0,b>0,b\ne 1,
y={\mathrm{log}}_{b}\left(x\right)\text{ ist gleich }{b}^{y}=x, wobei
- Wir lesen {\mathrm{log}}_{b}\left(x\right) als, „der Logarithmus zur Basis b von x“ oder die „logarithmische Basis b von x.“
- Der Logarithmus y ist der Exponent, auf den b erhöht werden muss, um x zu erhalten.
- Wenn keine Basis b angegeben ist, wird die Basis des Logarithmus mit 10 angenommen.
Da die Logarithmus- und die Exponentialfunktion die x- und y-Werte vertauschen, werden auch die Domäne und der Bereich der Exponentialfunktion für die logarithmische Funktion vertauscht. Deshalb,
- der Bereich der Logarithmusfunktion zur Basis b \text{ ist} \left(0,\infty \right).
- der Bereich der Logarithmusfunktion zur Basis b \text{ ist} \left(-\infty ,\infty \right).
Q & A
Kann man den Logarithmus einer negativen Zahl bilden?
Nein. Da die Basis einer Exponentialfunktion immer positiv ist, kann keine Potenz dieser Basis jemals negativ sein. Wir können niemals den Logarithmus einer negativen Zahl bilden. Wir können auch nicht den Logarithmus von Null nehmen. Taschenrechner können im komplexen Modus einen Logarithmus einer negativen Zahl ausgeben, aber der Logarithmus einer negativen Zahl ist keine reelle Zahl.
Hilfe: Wandeln Sie eine Gleichung in logarithmischer Form {\mathrm{log}}_{b}\left(x\right)=y in die Exponentialform um
- Untersuchen Sie die Gleichung y={\mathrm{log}}_{b}x und identifizieren Sie b, y und x.
- Schreiben Sie {\mathrm{log}}_{b}x=y als {b}^{y}=x um.
Beispiel: Umformung von der logarithmischen Form in die Exponentialform
Schreiben Sie die folgenden logarithmischen Gleichungen in die Exponentialform.
- {\mathrm{log}}_{6}\left(\sqrt{6}\right)=\frac{1}{2}
- {\mathrm{log}}_{3}\left(9\right)=2
Versuch es
Schreibe die folgenden logarithmischen Gleichungen in Exponentialform.
- {\mathrm{log}}_{10}\left(1.000,000\rechts)=6
- {\mathrm{log}}_{5}\links(25\rechts)=2
Umwandeln von der Exponential- in die Logarithmusform
Um von der Exponential- in die Logarithmusform umzuwandeln, folgen wir denselben Schritten in umgekehrter Reihenfolge. Wir identifizieren die Basis b, den Exponenten x und die Ausgabe y. Dann schreiben wir x={\mathrm{log}}_{b}\left(y\right).
Beispiel: Umwandlung von der Exponentialform in die logarithmische Form
Schreiben Sie die folgenden Exponentialgleichungen in die logarithmische Form.
- {2}^{3}=8
- {5}^{2}=25
- {10}^{-4}=\frac{1}{10,000}
Versuchen Sie es
Schreiben Sie die folgenden Exponentialgleichungen in logarithmische Form.
- {3}^{2}=9
- {5}^{3}=125
- {2}^{-1}=\frac{1}{2}
Beitragen!
Verbessern Sie diese SeiteMehr erfahren