Álgebra universitaria
Resultados de aprendizaje
- Convertir de forma logarítmica a exponencial.
- Convertir de forma exponencial a logarítmica.
Para analizar la magnitud de los terremotos o comparar las magnitudes de dos terremotos diferentes, necesitamos ser capaces de convertir entre la forma logarítmica y la exponencial. Por ejemplo, supongamos que la cantidad de energía liberada por un terremoto es 500 veces mayor que la cantidad de energía liberada por otro. Queremos calcular la diferencia de magnitud. La ecuación que representa este problema es {10}^{x}=500 donde x representa la diferencia de magnitudes en la escala de Richter. Cómo resolveríamos x?
Aún no hemos aprendido un método para resolver ecuaciones exponenciales algebraicamente. Ninguna de las herramientas algebraicas comentadas hasta ahora es suficiente para resolver {10}^{x}=500. Sabemos que {10}^{2}=100 y {10}^{3}=1000, por lo que está claro que x debe ser algún valor entre 2 y 3 ya que y={10}^{x} es creciente. Podemos examinar una gráfica para estimar mejor la solución.
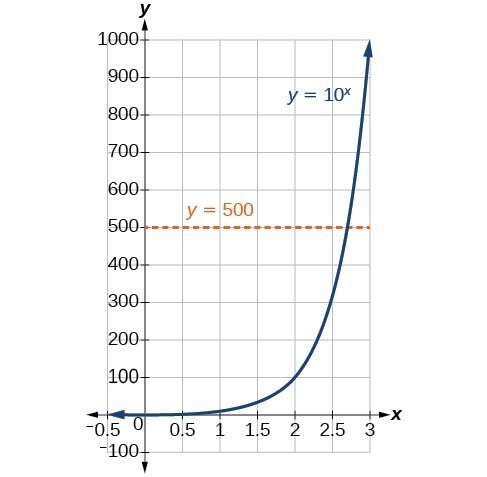
Estimar a partir de una gráfica, sin embargo, es impreciso. Para encontrar una solución algebraica, debemos introducir una nueva función. Observa que la gráfica anterior pasa la prueba de la línea horizontal. La función exponencial y={b}^{x} es uno a uno, por lo que su inversa, x={b}^{y}, también es una función. Como ocurre con todas las funciones inversas, simplemente intercambiamos x e y y resolvemos para y para encontrar la función inversa. Para representar y como una función de x, utilizamos una función logarítmica de la forma y={\mathrm{log}}_{b} {left(x\right)). El logaritmo de base b de un número es el exponente por el que debemos elevar b para obtener ese número.
Leemos una expresión logarítmica como, «El logaritmo con base b de x es igual a y», o, simplificado, «log base b de x es y». También podemos decir, «b elevado a la potencia de y es x», porque los logaritmos son exponentes. Por ejemplo, el logaritmo de base 2 de 32 es 5, porque 5 es el exponente que debemos aplicar a 2 para obtener 32. Como {2}^{5}=32, podemos escribir {\mathrm{log}}_{2}32=5. Lo leemos como «el log de base 2 de 32 es 5.»
Podemos expresar la relación entre la forma logarítmica y su correspondiente forma exponencial como sigue:
{mathrm{log}_{b}{izquierda(x\ derecha)=y}{b}^{y}=x,{text{}b>0,b\ne 1
Nota que la base b es siempre positiva.
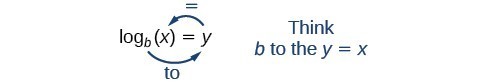
Debido a que un logaritmo es una función, lo más correcto es escribirlo como {{mathrm{log}}_{b}left(x\right) usando paréntesis para denotar la evaluación de la función tal y como lo haríamos con f\left(x\right). Sin embargo, cuando la entrada es una sola variable o número, es común ver los paréntesis eliminados y la expresión escrita sin paréntesis como {\mathrm{log}_{b}x. Tenga en cuenta que muchas calculadoras requieren paréntesis alrededor de la x.
Podemos ilustrar la notación de logaritmos de la siguiente manera:
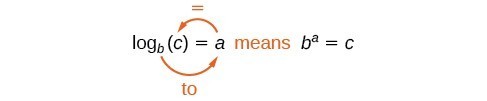
Nótese que al comparar la función logaritmo y la función exponencial, la entrada y la salida se intercambian. Esto quiere decir que y={mathrm{log}_{b} {left(x\right) y y={b}^{x} son funciones inversas.
Una nota general: definición de la función logarítmica
Un logaritmo base b de un número positivo x satisface la siguiente definición:
Para x>0,b>0,b\ne 1,
y={mathrm{log}}_{b}left(x\right)\text{}es igual a }{b}^{y}=x, donde
- leemos {{mathrm{log}}_{b}{left(x\right) como, «el logaritmo con base b de x» o el «log base b de x.»
- El logaritmo y es el exponente al que hay que elevar b para obtener x.
- Si no se indica la base b, se supone que la base del logaritmo es 10.
- el dominio de la función logaritmo con base b \text{ es} \left(0,\infty \right).
- el rango de la función logaritmo con base b \text{ es} \left(-\infty ,\infty \right).
Además, como las funciones logarítmica y exponencial intercambian los valores de x e y, el dominio y el rango de la función exponencial se intercambian para la función logarítmica. Por tanto,
¿Podemos tomar el logaritmo de un número negativo?
No. Como la base de una función exponencial es siempre positiva, ninguna potencia de esa base puede ser nunca negativa. Nunca podemos tomar el logaritmo de un número negativo. Tampoco podemos tomar el logaritmo de cero. Las calculadoras pueden dar el logaritmo de un número negativo cuando están en modo complejo, pero el logaritmo de un número negativo no es un número real.
Cómo: dada una ecuación en forma logarítmica {{mathrm{log}}_{b}left(x\right)=y, conviértela en forma exponencial
- Examina la ecuación y={mathrm{log}_{b}x e identifica b, y, y x.
- Reescribe {{mathrm{log}}_{b}x=y como {b}^{y}=x.
Ejemplo: Conversión de la forma logarítmica a la forma exponencial
Escribe las siguientes ecuaciones logarítmicas en forma exponencial.
- {mathrm{log}_{6}{left(\sqrt{6}{right)=\frac{1}{2}
- {mathrm{log}{3}{left(9\right)=2
Inténtalo
Escribe las siguientes ecuaciones logarítmicas en forma exponencial.
- {mathrm{log}_{10}{left(1,000,000\Nderecho)=6
- {mathrm{log}{5}\NIzquierda(25\Nderecho)=2
Convertir de forma exponencial a logarítmica
Para convertir de forma exponencial a logarítmica, seguimos los mismos pasos a la inversa. Identificamos la base b, el exponente x, y la salida y. Entonces escribimos x={mathrm{log}_{b}{left(y\right).
Ejemplo: Conversión de la forma exponencial a la forma logarítmica
Escribe las siguientes ecuaciones exponenciales en forma logarítmica.
- {2}^{3}=8
- {5}^{2}=25
- {10}^{4}=\frac{1}{10,000}
Inténtalo
Escribe las siguientes ecuaciones exponenciales en forma logarítmica.
- {3}^{2}=9
- {5}^{3}=125
- {2}^-1}=\frac{1}{2}
¡Contribuye!
Mejora esta páginaAprende más