Aplicaciones de los amplificadores operacionales
El primer ejemplo es el amplificador diferencial, del que se pueden derivar muchas de las otras aplicaciones, incluyendo el amplificador inversor, no inversor y sumador, el seguidor de tensión, el integrador, el diferenciador y el girador.
Amplificador diferencial (amplificador diferencial)

Amplifica la diferencia de tensión entre sus entradas.
No hay que confundir el nombre de «amplificador diferencial» con el de «diferenciador», que también aparece en esta página. El «amplificador de instrumentación», que también se muestra en esta página, es una modificación del amplificador diferencial que también proporciona una alta impedancia de entrada.
El circuito mostrado calcula la diferencia de dos tensiones, multiplicada por algún factor de ganancia. La tensión de salida
V out = ( R f + R 1 ) R g ( R g + R 2 ) R 1 V 2 – R f R 1 V 1 = ( R 1 + R f R 1 ) ⋅ ( R g R g + R 2 ) V 2 – R f R 1 V 1 . {\displaystyle V_{\text{out}}={\frac {\left(R_{\text{f}}+R_{1}\right)R_{\text{g}}}{\left(R_{\text{g}}+R_{2}\right)R_{1}}}V_{2}-{\frac {R_{\text{f}}}{R_{1}}}V_{1}=\left({\frac {R_{1}+R_{\text{f}}}{R_{1}}}\right)\cdot \left({\frac {R_{\text{g}}}{R_{\text{g}}+R_{2}}}\right)V_{2}-{\frac {R_{\text{f}}}{R_{1}}}V_{1}.}

O, expresado en función de la entrada en modo común Vcom y la entrada en diferencia Vdif:
V com = ( V 1 + V 2 ) / 2 ; V dif = V 2 – V 1 , {\displaystyle V_{text{com}=(V_{1}+V_{2})/2;V_{\text{dif}}=V_{2}-V_{1},}

La tensión de salida es
V out R 1 R f = V com R 1 / R f – R 2 / R g 1 + R 2 / R g + V dif 1 + ( R 2 / R g + R 1 / R f ) / 2 1 + R 2 / R g . {\displaystyle V_{\text{out}}{\frac {R_{1}}{R_{\text{f}}}}=V_{\text{com}}{\frac {R_{1}/R_{\text{f}}-R_{2}/R_{\text{g}}}{1+R_{2}/R_{\text{g}}}}+V_{\text{dif}}{\frac {1+(R_{2}/R_{\text{g}}+R_{1}/R_{\text{f}})/2}{1+R_{2}/R_{\text{g}}}}.}

Para que este circuito produzca una señal proporcional a la diferencia de tensión de los terminales de entrada, el coeficiente del término Vcom (la ganancia en modo común) debe ser cero, o
R 1 / R f = R 2 / R g . {\displaystyle R_{1}/R_{text{f}=R_{2}/R_{text{g}}.

Con esta restricción, la relación de rechazo en modo común de este circuito es infinitamente grande, y la salida
V out = R f R 1 V dif = R f R 1 ( V 2 – V 1 ) , {\displaystyle V_{\text{out}}={\frac {R_{\text{f}}}{R_{1}}}V_{\text{dif}}={\frac {R_{\text{f}}}{R_{1}}}\left(V_{2}-V_{1}\right),}

donde la sencilla expresión Rf / R1 representa la ganancia en lazo cerrado del amplificador diferencial.
El caso especial cuando la ganancia en lazo cerrado es la unidad es un seguidor diferencial, con
V out = V 2 – V 1 . {\displaystyle V_{\text{out}}=V_{2}-V_{1}.}

Amplificador inversorEditar
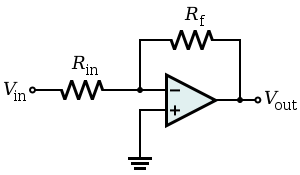
Un amplificador inversor es un caso especial del amplificador diferencial en el que la entrada no inversora de ese circuito, V2, está conectada a tierra, y la entrada inversora, V1, se identifica con Vin arriba. La ganancia en lazo cerrado es Rf / Rin, por lo tanto
V out = – R f R in V in {{displaystyle V_{text{out}}=-{{frac {R_{text{f}}{R_{text{in}}}}V_{text{in}}\,}

.
El circuito simplificado anterior es como el amplificador diferencial en el límite de R2 y Rg muy pequeño. Sin embargo, en este caso, el circuito será susceptible a la deriva de la corriente de polarización de entrada debido al desajuste entre Rf y Rin.
Para ver intuitivamente la ecuación de ganancia anterior, calcule la corriente en Rin:
i in = V en R en {{displaystyle i_{text{in}}={{frac} {V_{text{in}}{R_{text{in}}}}}}}

entonces recuerda que esta misma corriente debe estar pasando por Rf, por lo tanto (porque V- = V+ = 0):
V out = – i in R f = – V in R f R in {displaystyle V_{text{out}=-i_{text{in}}R_{text{f}=V_{text{in}}frac {R_{text{f}}}}}}}

Una analogía mecánica es un balancín, con el nodo V- (entre Rin y Rf) como punto de apoyo, a potencial de tierra. Vin está a una longitud Rin del punto de apoyo; Vout está a una longitud Rf. Cuando Vin desciende «por debajo de tierra», la salida Vout aumenta proporcionalmente para equilibrar el balancín, y viceversa.
Como la entrada negativa del amplificador óptico actúa como tierra virtual, la impedancia de entrada de este circuito es igual a Rin.
Amplificador no inversorEditar
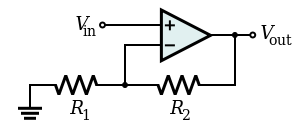
Un amplificador no inversor es un caso especial del amplificador diferencial en el que la entrada inversora V1 de ese circuito está conectada a tierra, y la entrada no inversora V2 se identifica con Vin arriba, con R1 ≫ R2.Refiriéndonos al circuito inmediatamente anterior,
V out = ( 1 + R 2 R 1 ) V in {\displaystyle V_{{text{out}}=left(1+{\frac {R_{text{2}}{R_{text{1}}}}}right)V_{{text{in}}.\,}

.
Para ver intuitivamente esta ecuación de ganancia, utilice la técnica de tierra virtual para calcular la corriente en la resistencia R1:
i 1 = V en R 1 , {\displaystyle i_{1}={frac {V_{text{in}}{R_{1}},,}

Entonces recuerda que esta misma corriente debe estar pasando por R2, por lo tanto:
V out = V in + i 1 R 2 = V in ( 1 + R 2 R 1 ) {\displaystyle V_{texto{out}=V_{texto{in}+i_{1}R_{2}=V_{texto{in} {{dirección}(1+{frac {R_{2}}{R_{1}}{dirección})}

A diferencia del amplificador inversor, un amplificador no inversor no puede tener una ganancia inferior a 1.
Una analogía mecánica es una palanca de clase 2, con un terminal de R1 como punto de apoyo, a potencial de tierra. Vin está en una longitud R1 desde el punto de apoyo; Vout está en una longitud R2 más adelante. Cuando Vin asciende «por encima de tierra», la salida Vout aumenta proporcionalmente con la palanca.
La impedancia de entrada del amplificador simplificado no inversor es alta:
Z in = ( 1 + A OL B ) Z dif {\displaystyle Z_{text{in}}=(1+A_{text{OL}}B)Z_{text{dif}}

donde Zdif es la impedancia de entrada del op-amp a las señales diferenciales, y AOL es la ganancia de tensión en bucle abierto del op-amp (que varía con la frecuencia), y B es el factor de realimentación (la fracción de la señal de salida que vuelve a la entrada). En el caso del amplificador óptico ideal, con AOL infinito y Zdif infinito, la impedancia de entrada también es infinita. En este caso, sin embargo, el circuito será susceptible a la deriva de la corriente de polarización de entrada debido a la falta de coincidencia entre las impedancias que conducen a las entradas V+ y V- del op-amp.
El bucle de realimentación disminuye de manera similar la impedancia de salida:
Z out = Z OL 1 + A OL B {\displaystyle Z_{text{out}={\frac {Z_{text{OL}}{1+A_{text{OL}}B}}

donde Zout es la impedancia de salida con realimentación, y ZOL es la impedancia de salida en bucle abierto.
Seguidor de tensión (amplificador de ganancia unitaria)Editar

Se utiliza como un amplificador buffer para eliminar los efectos de carga (por ejemplo, conectando un dispositivo con una alta impedancia de fuente a un dispositivo con una baja impedancia de entrada).
V out = V in {{displaystyle V_{text{out}}=V_{text{in}}

Z in = ∞ {{displaystyle Z_{text{in}}={infty}}

(de forma realista, la impedancia de entrada diferencial del propio amplificador operacional (1 MΩ a 1 TΩ), multiplicada por la ganancia en bucle abierto del amplificador operacional)
Debido a la retroalimentación fuerte (es decir, ganancia unitaria) y a ciertas características no ideales de los amplificadores operacionales reales, este sistema de retroalimentación es propenso a tener márgenes de estabilidad pobres. En consecuencia, el sistema puede ser inestable cuando se conecta a cargas suficientemente capacitivas. En estos casos, se puede utilizar una red de compensación de retardo (por ejemplo, conectando la carga al seguidor de tensión a través de una resistencia) para restaurar la estabilidad. La hoja de datos del fabricante del amplificador operacional puede servir de guía para la selección de los componentes de las redes de compensación externas. Alternativamente, se puede elegir otro amplificador operacional que tenga una compensación interna más adecuada.
La impedancia de entrada y de salida se ven afectadas por el bucle de realimentación de la misma manera que el amplificador no inversor, con B=1.
Amplificador sumadorEditar
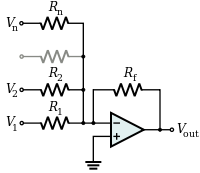
Un amplificador sumador suma varias tensiones (ponderadas):
V out = – R f ( V 1 R 1 + V 2 R 2 + ⋯ + V n R n ) {\displaystyle V_{text{out}=-R_{{text{f}}left({{frac {V_{1}}{R_{1}}+{{frac {V_{2}}+{cdots +{frac {V_{n}}right)}

- Cuando R 1 = R 2 = ⋯ = R n {{displaystyle R_{1}=R_{2}={cdots =R_{n}}
, y R f {\displaystyle R_{text{f}}
independiente V out = – R f R 1 ( V 1 + V 2 + ⋯ + V n ) {\displaystyle V_{text{out}=-{\frac {R_{text{f}}{R_{1}}(V_{1}+V_{2}+\cdots +V_{n})}} ¡
- Cuando R 1 = R 2 = ⋯ = R n = R f {\displaystyle R_{1}=R_{2}=\cdots =R_{n}=R_{text{f}}
V out = – ( V 1 + V 2 + ⋯ + V n ) {\displaystyle V_{{text{out}}=-(V_{1}+V_{2}+\cdots +V_{n})¡!
- La salida está invertida
- La impedancia de entrada de la nª entrada es Z n = R n {displaystyle Z_{n}=R_{n}}.
( V – {\displaystyle V_{-}
es una tierra virtual)
Amplificador de instrumentaciónEdit
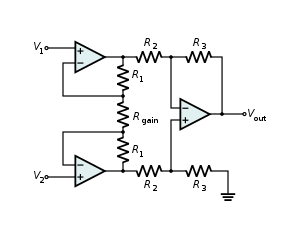
- Cuando R 1 = R 2 = ⋯ = R n = R f {\displaystyle R_{1}=R_{2}=\cdots =R_{n}=R_{text{f}}






