Backpropagation Paso a Paso
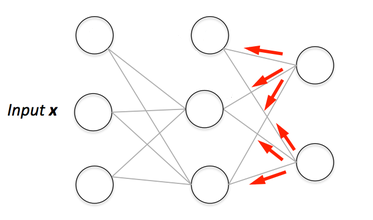Si estás construyendo tu propia red neuronal, definitivamente necesitarás entender cómo entrenarla.Backpropagation es una técnica comúnmente usada para entrenar redes neuronales. Hay muchos recursos que explican la técnica, pero este post explicará la retropropagación con un ejemplo concreto en unos pasos muy detallados y coloridos.
Puedes ver la visualización del pase hacia adelante y la retropropagación aquí. Puedes construir tu red neuronal usando netflow.js
Resumen
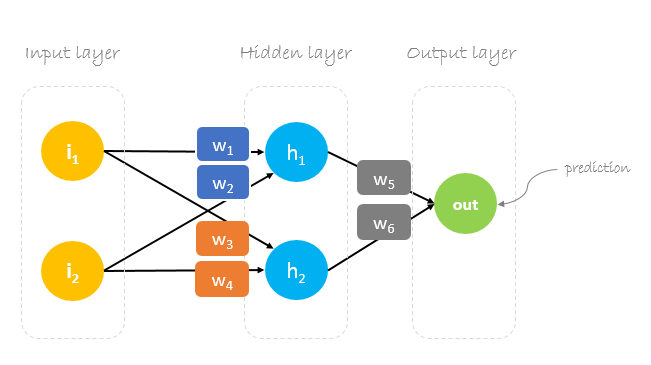
En este post, construiremos una red neuronal con tres capas:
- Capa de entrada con dos neuronas de entrada
- Una capa oculta con dos neuronas
- Capa de salida con una sola neurona
Pesos, pesos, pesos
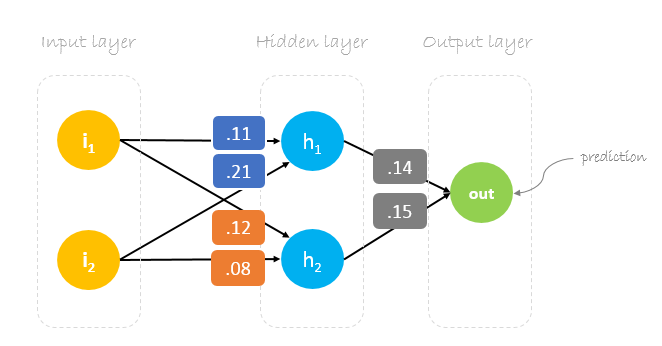
El entrenamiento de una red neuronal consiste en encontrar los pesos que minimicen el error de predicción. Por lo general, comenzamos nuestro entrenamiento con un conjunto de pesos generados al azar.Luego, la retropropagación se utiliza para actualizar los pesos en un intento de asignar correctamente entradas arbitrarias a las salidas.
Nuestros pesos iniciales serán los siguientes:w1 = 0.11w2 = 0.21w3 = 0.12w4 = 0.08w5 = 0.14 y w6 = 0.15
Conjunto de datos
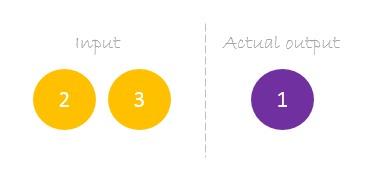
Nuestro conjunto de datos tiene una muestra con dos entradas y una salida.
Nuestra única muestra es la siguiente inputs= y output=.
Paso adelante
Utilizaremos los pesos y las entradas dadas para predecir la salida. Las entradas se multiplican por los pesos; los resultados se pasan a la siguiente capa.
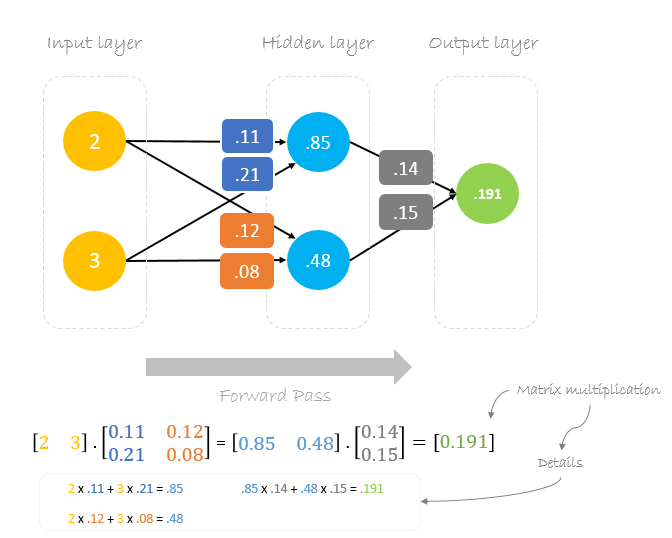
Calcular el error
Ahora, es el momento de averiguar cómo ha funcionado nuestra red calculando la diferencia entre la salida real y la predicha. Está claro que la salida de nuestra red, o predicción, no se acerca ni de lejos a la salida real. Podemos calcular la diferencia o el error de la siguiente manera.
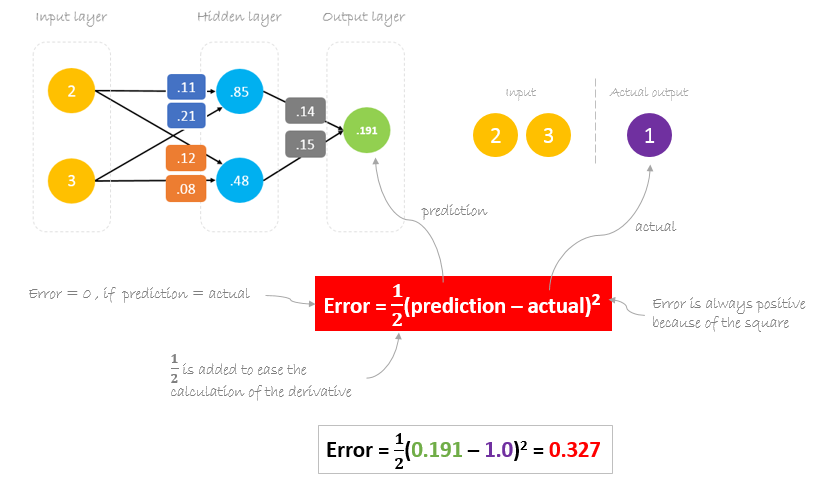
Reducir el error
Nuestro principal objetivo del entrenamiento es reducir el error o la diferencia entre la predicción y la salida real. Como la salida real es constante, «no cambia», la única forma de reducir el error es cambiar el valor de la predicción. La pregunta ahora es, ¿cómo cambiar el valor de la predicción?
Descomponiendo la predicción en sus elementos básicos podemos encontrar que los pesos son los elementos variables que afectan al valor de la predicción. En otras palabras, para cambiar el valor de la predicción, necesitamos cambiar los valores de los pesos.
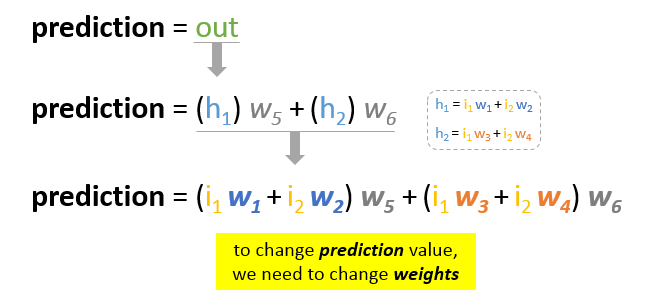
La pregunta ahora es ¿cómo cambiar el valor de los pesos para que el error se reduzca?
¡La respuesta es Backpropagation!
Backpropagation
Backpropagation, abreviatura de «backward propagation of errors», es un mecanismo utilizado para actualizar los pesos utilizando el descenso de gradiente. Calcula el gradiente de la función de error con respecto a los pesos de la red neuronal. El cálculo procede hacia atrás a través de la red.
El descenso de gradiente es un algoritmo de optimización iterativo para encontrar el mínimo de una función; en nuestro caso queremos minimizar la función de error. Para encontrar un mínimo local de una función utilizando el descenso de gradiente, se dan pasos proporcionales al negativo del gradiente de la función en el punto actual.
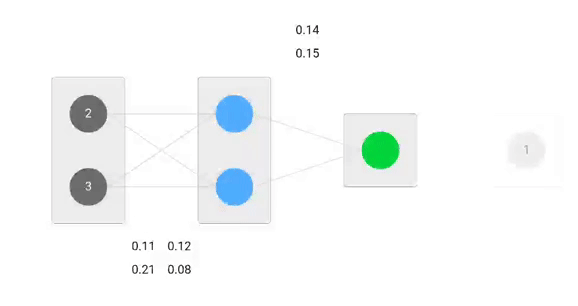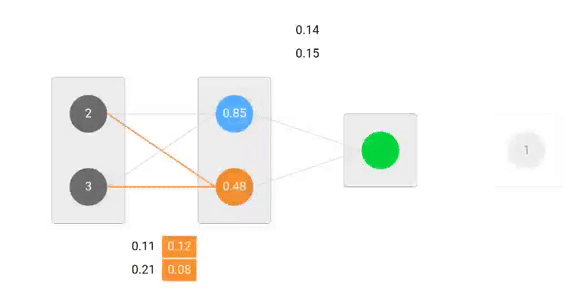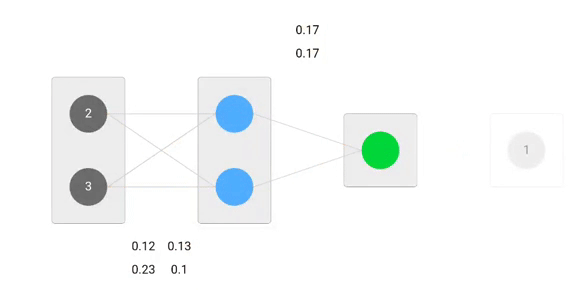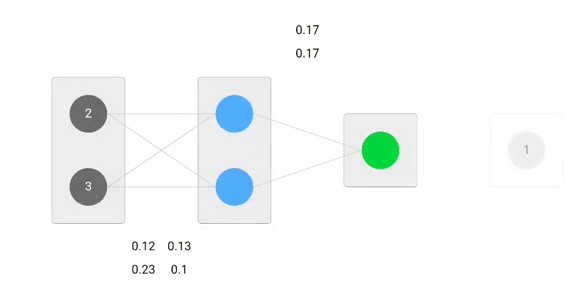
Por ejemplo, para actualizar w6, tomamos el w6 actual y le restamos la derivada parcial de la función de error con respecto a w6. Opcionalmente, multiplicamos la derivada de la función de error por un número seleccionado para asegurarnos de que el nuevo peso actualizado está minimizando la función de error; este número se llama tasa de aprendizaje.
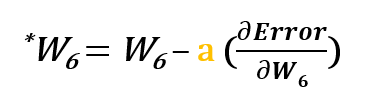
La derivada de la función de error se evalúa aplicando la regla de la cadena de la siguiente manera
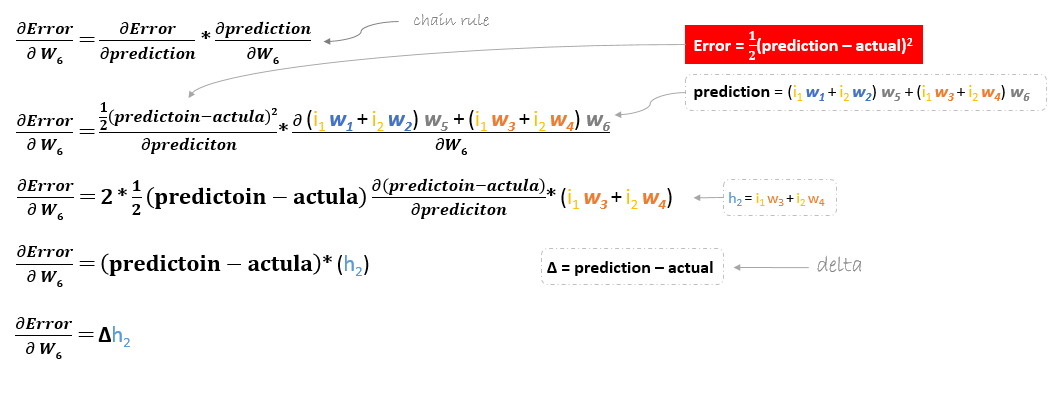
Así que para actualizar w6 podemos aplicar la siguiente fórmula
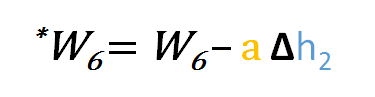
De forma similar, podemos derivar la fórmula de actualización para w5 y cualquier otro peso existente entre la salida y la capa oculta.
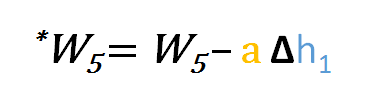
Sin embargo, al retroceder para actualizar w1w2w3 y w4 existentes entre la entrada y la capa oculta, la derivada parcial para la función de error con respecto a w1, por ejemplo, será la siguiente.
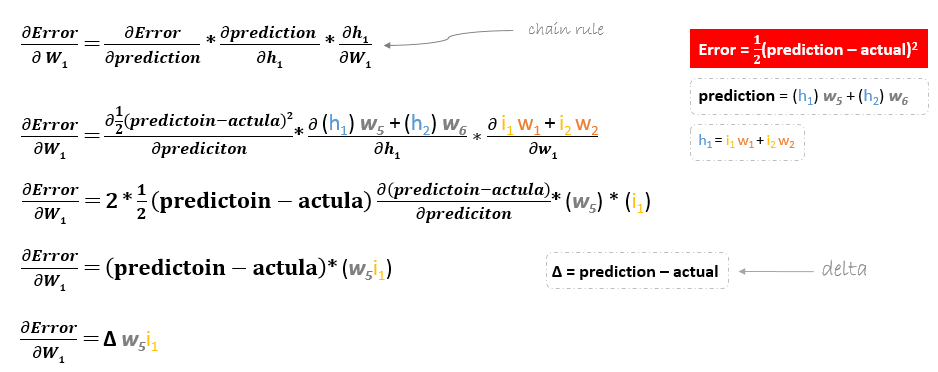
Podemos encontrar la fórmula de actualización para el resto de pesos w2w3 y w4 de la misma manera.
En resumen, las fórmulas de actualización de todos los pesos serán las siguientes:
Podemos reescribir las fórmulas de actualización en matrices como sigue
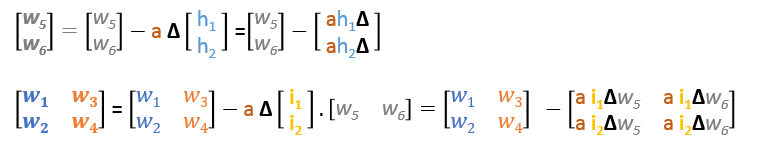
Paso hacia atrás
Utilizando las fórmulas derivadas podemos encontrar los nuevos pesos.
Tasa de aprendizaje: es un hiperparámetro lo que significa que tenemos que adivinar manualmente su valor.
Ahora, usando los nuevos pesos repetiremos el forward pasado
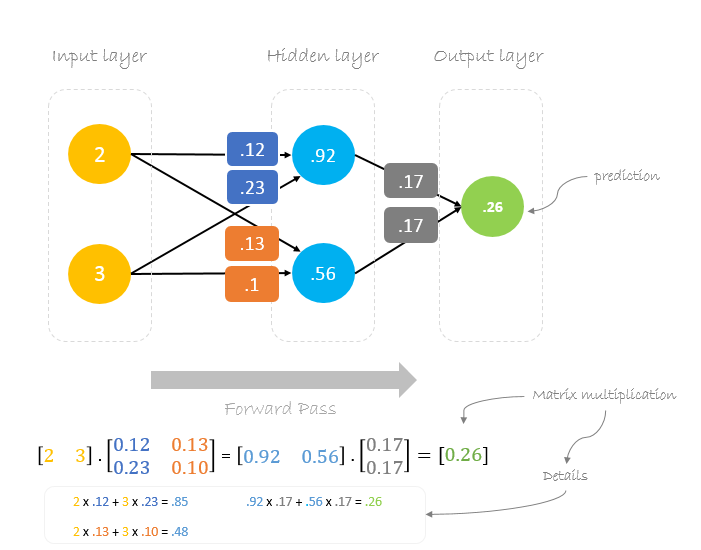
Podemos observar que la predicción 0.26 se acerca un poco más a la salida real que la predicha anteriormente 0.191. Podemos repetir el mismo proceso de pase hacia atrás y hacia adelante hasta que el error se acerque o sea igual a cero.
Visualización de la retropropagación
Puedes ver la visualización del pase hacia adelante y la retropropagación aquí.
Puedes construir tu red neuronal usando netflow.js
