Cristalografía. Dispersión y difracción. La Ley de Bragg
Si, tras la reflexión, las ondas emergentes están en fase, se observará la intensidad reflejada, es decir, se cumple la Ley de Bragg.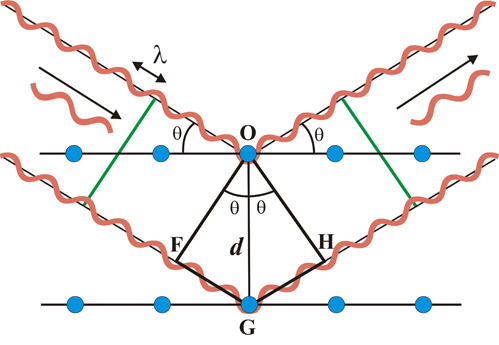 Como se demostró con las ecuaciones de Laue, la Ley de Bragg propuesta por ambos, padre e hijo (WilliamH. Bragg y WilliamL. Bragg), también puede derivarse gráficamente de forma sencilla…
Como se demostró con las ecuaciones de Laue, la Ley de Bragg propuesta por ambos, padre e hijo (WilliamH. Bragg y WilliamL. Bragg), también puede derivarse gráficamente de forma sencilla…
La hipótesis es imaginar la difracción de Bragg como un reflejo de los rayos X en la superficie de «espejos» imaginarios formados por planos atómicos en la red cristalina (mostrados como líneas horizontales que contienen los centros de dispersión, es decir, los átomos mostrados como círculos azules en la imagen de la izquierda). Debido a la naturaleza repetitiva del cristal, estos planos estarían separados por una distancia constante d.
Los dos haces de rayos X de longitud de onda λ, llegan en fase a los respectivos planos imaginarios, con un ángulo deincidencia θ, y forman un frente de onda (línea verde a la izquierda).
Para obtener un efecto cooperativo, después de la reflexión ambos rayos X deben seguir en fase (línea verde de la derecha), situación que sólo se producirá si la diferencia de camino recorrido por los frentes de onda OF y OH (frentes de onda antes y después de la reflexión) se corresponde con un número entero de longitudes de onda.
Esta condición equivale a decir que la suma de los segmentos FGy GH corresponde a un número entero (n)de veces la longitud de onda (λ):
y por tanto la expresión (1)se convierte en:
Esta es la Ley de Bragg.
Si las ondas reflejadas emergentes tienen fase opuesta, no se observará intensidad reflejada, es decir, no se cumple la Ley de Bragg.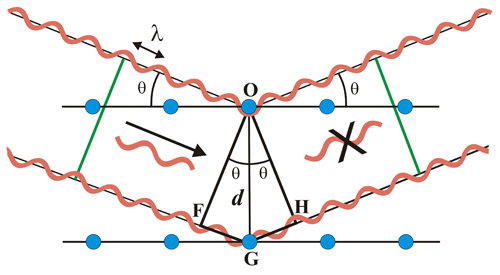 Cuando el ángulo de incidencia de los rayos X no satisface la Ley de Bragg, los haces emergentes no están en fase (línea verde a la derecha), y se cancelan mutuamente, por lo que no se observará ninguna intensidad reflejada.
Cuando el ángulo de incidencia de los rayos X no satisface la Ley de Bragg, los haces emergentes no están en fase (línea verde a la derecha), y se cancelan mutuamente, por lo que no se observará ninguna intensidad reflejada.
Si consideramos el escenario base y observamos cuidadosamente la Ley de Bragg, es fácil darse cuenta de que: