¿Cuál es el número más grande?

Los números son eternos, pero en el camino hacia el infinito hay algunos puestos bastante remotos.

Para nuestros antepasados, un millón era lo más grande que podían llegar a ser los números. No era necesario invocar los miles de millones (1.000.000.000) de las finanzas o los terabytes (1012) de la informática. La tecnología nos ha vuelto indiferentes al uso de números de 9 o 12 dígitos en las conversaciones. Sin embargo, aún falta mucho para que nos pongamos al día con la escala de nuestro lugar en el universo, por no hablar de los vertiginosos números gigantescos que han soñado los matemáticos.

Números estándar

Más allá de los mil millones -el orden de magnitud de la población humana- tenemos que decir adiós a la idea de tener nombres para los números. (Aunque existen hasta 1063, no son de uso común). Para la distancia que recorre la luz en un minuto, el número de átomos en un gramo de carbono o la distancia entre galaxias, los científicos utilizan la forma estándar para expresarse. La forma estándar registra todos los números en el formato a × 10n, donde a es un número entre 1 y 10 y n puede ser cualquier número. Es lo que se usaría para hablar del número de átomos de carbono en una muestra de 12g. Que, por cierto, es 6,22 × 1023, el número de Avogadro, y bastante grande. El universo observable tiene unos 8,8 × 1023 km de ancho, y se calcula que hay unas 1087 partículas en él. Pero más grandes que esos números son, con mucho, las construcciones de las mentes matemáticas.

Déjame que lo googlee

Inmortalizado en el uso común por el gigante de internet, un googol es el número 10100 – 10, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000. El matemático estadounidense Edward Kasner pidió a su sobrino Milton que le pusiera nombre, y se convirtió en un googol. Pero el siguiente número realmente grande es el gúgolplex, que eleva 10 a la potencia de un gúgol. Esto es astronómicamente más grande que un gúgol – es imposible escribir un gúgolplex en notación estándar incluso si se escribe un solo dígito en cada partícula del universo.

El poder de las potencias

Adiendo un exponente en el exponente realmente aumenta la tasa de ampliación de los números.

3×3×3=27

3(33) = 7,625,597,484,987

Naturalmente, en la búsqueda de números más grandes, uno añadiría más y más potencias a la torre. Sin embargo, esto se vuelve rápidamente incómodo de escribir, además de dar lugar a torres que hacen que la de Pisa parezca estable. El cambio de notación permite condensar estas torres y expresar conceptos más elevados.

Sigue las flechas

Desarrollando otra forma de denotar potencias:

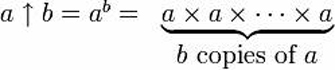
Donald Knuth acuñó un nuevo operador para la exponenciación repetida («tetration»), para bajar esas torres de potencia a la tierra.

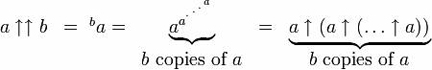
En uso, la doble flecha tiene este aspecto:

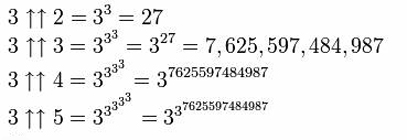
Se puede ampliar aún más añadiendo una tercera flecha, creando la operación de «pentación» – tetración repetida.

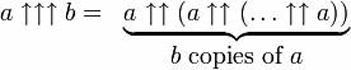
En palabras, eso implica tetrar a la a (así, una torre de potencia de a ‘a’s), luego construir otra torre de ‘a’s tan alta como esa torre de potencia, luego usar el resultado de esa torre de potencia para determinar el número de ‘a’s en la siguiente -resultando en el cálculo de b torres de potencia, aumentando en altura según el resultado de la tetración anterior.

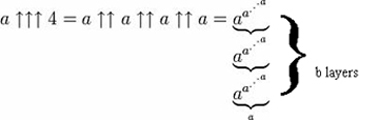
Y aún se pueden añadir más flechas, aunque pensar en las operaciones que denotan puede requerir más tiempo cerebral del que estás dispuesto a dedicar al asunto. Pero armados con esta notación, ahora podemos reconocer algunos números verdaderamente grandes.

Llamando a Ackermann y Graham

Las pruebas matemáticas nos han dado algunas cantidades masivas. A principios del siglo XX, los matemáticos querían saber cómo saber si una secuencia era computable: ¿podría definirse un proceso mecánico para elaborarla? Se propuso que una secuencia era computable si tenía la propiedad de ser «recursiva primitiva». Wilhelm Ackermann echó un cable en forma de secuencia al acuñar una secuencia que, aunque era computable, no era recursiva primitiva. Y dice así:

Comience con la operación matemática más simple posible – la suma. Aplícala al primer número natural, el 1:

1 + 1 = 2

Después pasa a la siguiente operación, la multiplicación (suma repetida). Hazlo con el siguiente número:

2 × 2 = 4

El siguiente paso es la multiplicación repetida -exponenciación para ti y para mí- con el 3 como variable.

33 = 27

Hasta aquí, tan insignificante. Pero acabamos de definir una función para la exponenciación repetida, la tetrada, y si hacemos esto a 4..

Se ve pequeño, tiene 10154 dígitos. Y éste es sólo el cuarto término de la secuencia.

El quinto es … una torre de potencia de cinco dígitos de altura.

El sexto es . Sólo cinco símbolos denotan un número más grande de lo que cabe en el universo, incluso si escribieras cada dígito en una fuente de 1nm de ancho. Y la secuencia continúa.

La misma notación de flecha hacia arriba fue utilizada por Ronald Graham para limitar algunas propiedades de un hipercubo (un cubo en 4 dimensiones espaciales), aunque el ‘número de Graham’ es ahora más conocido simplemente por ser colosal.

El número de Graham se define así:

El número de flechas de cada capa viene dado por el resultado de evaluar las flechas de la capa de abajo, hasta que después de 64 capas, se alcanza el número final. Para hacernos una idea de su tamaño, podemos fijarnos sólo en la primera capa:

donde el número de tres en la expresión de la derecha es

Ahora cada operación de tetración () se reduce a una «torre» de exponencias () según la definición

donde hay X tres.

Así,

donde el número de tres es , se convierte, únicamente en términos de «torres de exponenciación» repetidas, y donde el número de treses en cada torre, empezando por la torre más a la izquierda, está especificado por el valor de la siguiente torre a la derecha.

Eso es, técnicamente hablando, un montón de treses. Sin embargo, no te relajes todavía, ya que el número de Graham, a pesar de ser el mayor número que los matemáticos han necesitado escribir explícitamente hasta ahora, se ve empequeñecido por algunos productos de la teoría de la computación. No tenemos espacio para hablar de ellos aquí, pero eche un vistazo a «¿Quién puede escribir el número más grande?», de Scott Aaronson, si el número de Graham no es suficiente para usted. También profundiza en la historia de los números grandes y sus explicaciones.

Grandes, más grandes, más grandes

El mundo de los números es, como cabría esperar, infinito. La naturaleza es bastante grande, pero los números que nos exige son mucho más pequeños que los que los matemáticos humanos han soñado. En ese sentido, la mente humana es más grande que el universo.