Ecuaciones de pandeo de columnas y comportamiento de pandeo | DegreeTutors.com

En el último post de esta serie, introdujimos algunos conceptos básicos utilizando una estructura idealizada simplificada. En esta entrada empezaremos a considerar estructuras más realistas y determinaremos las ecuaciones de pandeo de las columnas. En particular, determinaremos una expresión para la carga crítica de un pilar cargado axialmente con los extremos fijados. Luego exploraremos algunas otras condiciones de apoyo.

📓 Este post es la segunda parte de una serie de tres partes sobre el pandeo de columnas. Puede descargar la serie completa de tres partes, bien formateada y tipografiada en un libro electrónico de forma gratuita.

Cubriremos mucho en este, así que aquí está la tabla de contenidos…

Columnas clavadas en ambos extremos
Establecimiento de la ecuación diferencial
Resolución de la ecuación diferencial
Resolución de las constantes de integración
.
Modos de pandeo y formas de los modos
Máxima deflexión bajo carga crítica
Modos de pandeo de orden superior
Pilares con otras condiciones de apoyo
Fijado-.Fijo
Fijo-Libre
Fijo-Pinzado
Eje de pandeo
Esfuerzo crítico
Longitud efectiva del pilar

Cuando nos referimos a un apoyo pin, se trata de un apoyo que no ofrece resistencia al giro. A veces nos encontramos en la práctica con apoyos de pasador que se aproximan mucho a esta definición teórica. He aquí algunos ejemplos:

Para los fines de nuestra discusión aquí, supondremos que estamos tratando con soportes de pasador como estos, y que no inhiben la rotación de la estructura.

1.0 Ecuación de pandeo para pilares con pernos en ambos extremos

Para analizar esta estructura, vamos a utilizar la ecuación diferencial de la curva de deformación en la que es el momento flector interno en una sección dada, representa la deflexión lateral del pilar y la distancia a lo largo del pilar. se denomina rigidez a la flexión y es el producto del módulo de Young y el segundo momento del área de la sección transversal .

$\begin{align*}EI\frac{\mathrm{d}^2v}{\mathrm{dx^2}}=M\end{align*}$

Esta ecuación simplemente modela la forma deflectada de la columna para una rigidez de flexión dada.

Es probable que te hayas encontrado con esta ecuación en otra parte de tus estudios de ingeniería. Nuestra columna deflectada lateralmente se comporta de forma muy parecida a una viga. Recuerda que el pandeo es una falla por flexión en lugar de una falla por compresión directa (aplastamiento). Nuestra tarea ahora, es utilizar esta ecuación para derivar una expresión para la carga axial crítica en una columna con extremo de pino.

📌 Al igual que para la estructura idealizada discutida en el post anterior, nuestra derivación aquí también asumirá que todas las deflexiones son pequeñas en comparación con el tamaño de la estructura.

Establecimiento de la ecuación diferencial

Primero considera la estructura, su forma deflectada y el diagrama de cuerpo librecuerpo libre que resulta de cortar la estructura a una distancia del soporte inferior…

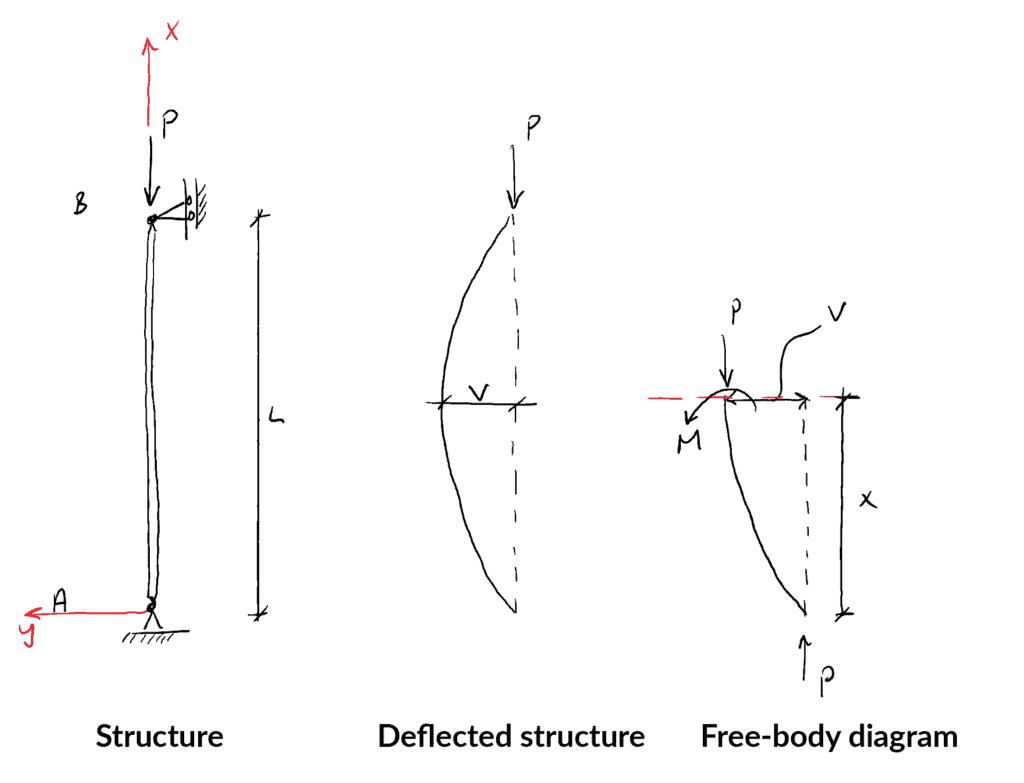
Tomando los momentos sobre el punto A se obtiene:

$\begin{align*}M=-Pv\end{align*}$

Sustituyendo de nuevo en la ecuación diferencial de la curva de desviación y reordenando ligeramente se obtiene:

$\begin{align*}\frac{{mathrm{d}^2v}{mathrm{d}x^2} + \frac{P}{EI}v=0\final{align*}$

Esta es una ecuación diferencial lineal, homogénea, de 2º orden con coeficientes constantes. También resulta ser una ecuación que modela la forma desviada de nuestra estructura y contiene , la carga axial. Siguiendo el mismo planteamiento que para la estructura idealizada comentada anteriormente, si resolvemos esta ecuación podemos determinar $P_{cr}$ , el valor de la carga aplicada a la que se equilibra con la resistencia a flexión de la columna.

Así que nos enfrentamos a intentar resolver una ecuación diferencial. En este punto, es útil poder señalar la solución general de esta forma de ecuación diferencial:

$\begin{align*}v(x) = C_1 \sin\left(\sqrt{\frac{P}{EI}}x\right) + C_2\cos\left(\sqrt{\frac{P}{EI}}x\right)\end{align*}$

Resolución de la ecuación diferencial

Si quieres dar un rodeo en este punto para ver cómo se resuelve la ecuación diferencial, mira el vídeo de abajo. Si no, seguiremos resolviendo las constantes de integración en el siguiente apartado.

Resolución de las constantes de integración

Ahora que tenemos la solución general para este formato de ecuación, tenemos que resolver las constantes de integración utilizando las condiciones de contorno (clavadas) de nuestra columna.

Condición de contorno 1:

En (base de la columna en el apoyo de los pines), (la deflexión lateral debe ser igual a cero. Imponiendo estas condiciones a nuestra solución general se obtiene:

$\begin{align*}0=C_1\sin(0) + C_2\cos(0)\end{align*}$ $\begin{align*}C_2=0\end{align*}$

Como resultado nuestra solución se reduce a:

$\begin{align*}v(x)=C_1sin \left(\sqrt{frac{P}{EI}xright)\end{align*}$

Condición límite 2:

En (parte superior de la columna en el apoyo del pasador), (la deflexión lateral también es nula). Nuevamente, imponiendo estas condiciones de contorno se obtiene,

$\begin{align*}0=C_1\\b\a la izquierda(\sqrt{frac{P}{EI}}la derecha)\bend{align*}$

Entonces, o bien es igual a cero o bien es igual a cero. Si es igual a cero, la ecuación se satisface para cualquier valor de . Esto realmente no nos hace avanzar… podemos pensar en esta solución como la solución trivial. Más interesante es el caso en el que:

$\begin{align*}\sin\left(\sqrt{\frac{P}{EI}}L\right)=0\end{align*}$

Sabiendo lo que sabemos sobre las funciones , esta ecuación sólo puede ser cierta, cuando,

$\begin{align*} {sqrt{frac{P}{EI}}L = 0, \pi, 2\pi,...n\pi\end{align*}$

Podemos descartar el caso en el que,

$begin{align*}sqrt{frac{P}{EI}}L = 0{end{align*}$

En este escenario, tendría que ser igual a cero (ya que todos los demás términos tienen valores distintos de cero por definición) y sabemos que no es así. Así que para una columna con anclaje, nuestra solución es:

$\begin{align*} {sqrt{frac{P}{EI}}L = n\pi\end{align*}$

donde … Finalmente, podemos reordenar esta ecuación para que sea el sujeto de la ecuación:

$\begin{align*}P=\frac{n^2\pi^2EI}{L^2}{end{align*}$

Para …

📌 Esta ecuación representa una serie infinita de cargas de pandeo. La más baja es la carga crítica de pandeo, también conocida como carga de pandeo de Euler .

$\begin{align*}P_E = \frac{pi^2EI}{L^2}end{align*}$

2.0 Modos de pandeo y formas modales

Hasta ahora, hemos establecido que existe una serie infinita de cargas de pandeo y que la más baja es la crítica y se llama carga de pandeo de Euler. Esto nos lleva a preguntarnos ¿a qué corresponden las cargas de pandeo mayores?

Son cargas que corresponden a modos de pandeo superiores. Cada modo de pandeo tiene una forma de pandeo correspondiente. Para explorar esto más a fondo, remítase a nuestra solución general después de establecer que :

$\begin{align*}v(x)=C_1\sin \left(\sqrt{\frac{P}{EI}}x\right)\end{align*}$

La aplicación de nuestra segunda condición de contorno nos permitió establecer la relación:

$\begin{align*}\sqrt{\frac{P}{EI}}L = n\pi\end{align*}$

Combinando estas dos ecuaciones se obtiene:

$\begin{align*}v(x)=C_1\sin\left(\frac{n\pi x}{L}\right)\nd{align*}$

para … Esta ecuación describe la forma deflectada del pilar para cada valor de la carga de pandeo definida anteriormente. Sólo cuando la carga axial tiene uno de los valores dados por la ecuación (previamente definida)…

$\begin{align*}P=\frac{n^2\pi^2EI}{L^2}end{align*}$

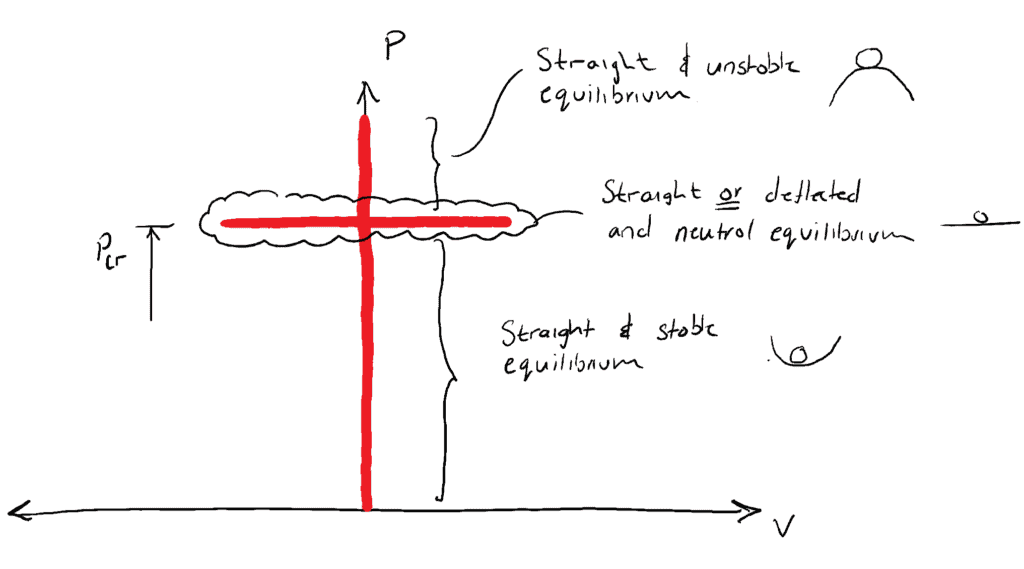
…la columna puede tener una forma doblada y estar en equilibrio. Para cualquier otra carga, la columna estaría recta y en un estado de equilibrio ESTABLE $(PP_{cr})$ o de equilibrio INESTABLE $(PP_{cr})$ . Recordamos este concepto de nuestra anterior discusión o estructuras de columnas idealizadas en el último post:

Máxima deflexión bajo carga crítica

Nuestra ecuación para la forma deflectada o pandeada de una columna contiene el parámetro , que nos queda de la solución general de la ecuación diferencial. Ahora reconocemos que representa la magnitud de la onda sinusoidal o, en este contexto, la deflexión lateral máxima para la deflexión/depresión (definida anteriormente):

$\begin{align*}v(x)=C_1\sin\left(\frac{n\pi x}{L}\right)\end{align*}$

Si ahora recordamos los estados de equilibrio, cuando la columna está en su forma abrochada $(P=P_{cr})$ y en un estado de equilibrio neutro, la deflexión lateral máxima puede tener cualquier valor que siga satisfaciendo nuestra hipótesis de deflexión pequeña. Podemos representar el valor de gráficamente…

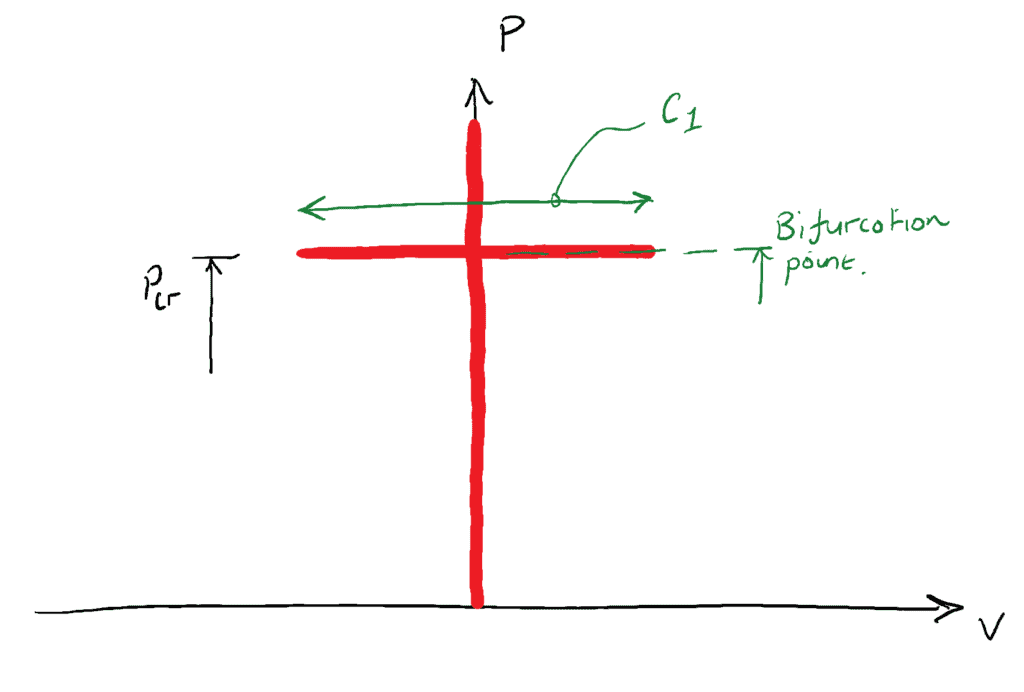
El valor de es por tanto matemáticamente indefinido, puede tener cualquier valor «pequeño». Afortunadamente, esto no nos causa ninguna dificultad práctica, ya que, como se ha mencionado anteriormente, el estado de equilibrio neutro no es algo que observemos en la práctica de la ingeniería civil. A todos los efectos, para un ingeniero civil o estructural, una columna que experimenta $P_{cr}$ se considera que ha fallado. Este estado teórico de equilibrio neutro también se conoce como punto de bifurcación.

Modos de pandeo de orden superior

Imagine un pilar con carga axial que está restringido lateralmente en su punto de altura media (por un forjado, por ejemplo). El pilar no podría pandearse bajo la primera carga crítica (pandeo de Euler) debido a la restricción lateral. La restricción del forjado sujeta literalmente el pilar y evita que se pandee.

Como resultado de esta restricción, el pilar puede soportar más carga, hasta que alcanza la segunda carga de pandeo . Como la columna no está restringida contra el pandeo en el segundo modo, ahora se pandearía (o teóricamente entraría en un estado de equilibrio neutro).

💡Una restricción lateral adecuada aumenta la resistencia de una columna al pandeo «cerrando» la posibilidad de pandeo en los modos inferiores y «desbloqueando» las cargas de pandeo superiores.

Podemos visualizar fácilmente los tres primeros modos de pandeo simplemente evaluando las ecuaciones de carga y forma deflectada para .

Modo

$\begin{align*}n=1\end{align*}$

$\begin{align*}n=2\end{align*}$ $\begin{align*}n=2\end{align*}$

$\n=3\nfinal$

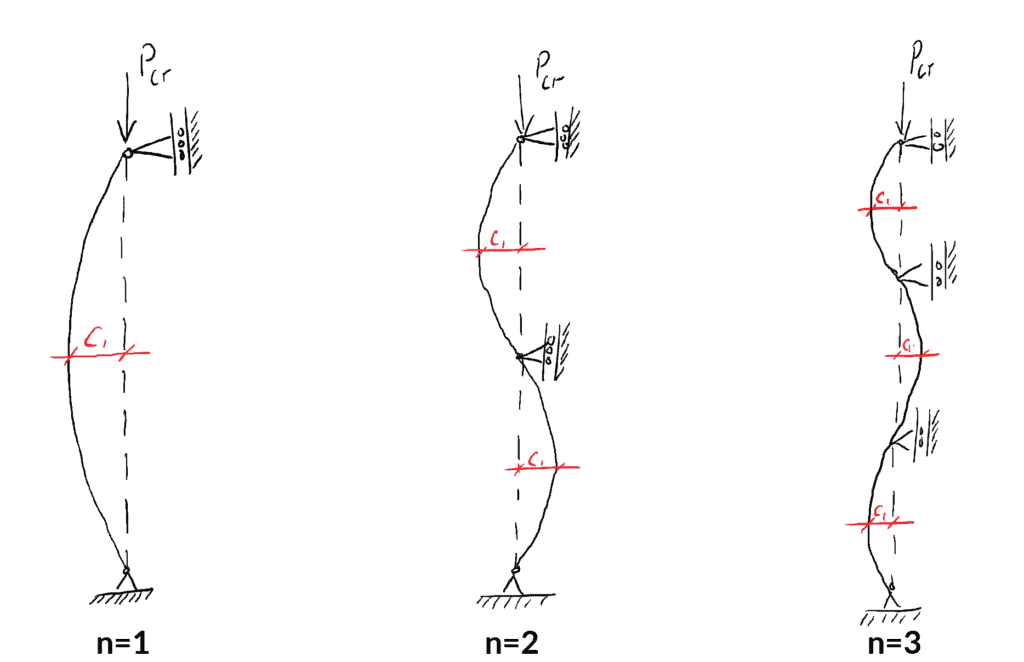
Carga crítica

$\Ndejar de ser P_{cr} = \Nfrac{pi^2EI}{L^2}end{align*}$

$dejar de ser P_{cr} =$ $\begin{align*}P_{cr} = \frac{9\pi^2EI}{L^2}\end{align*}$ $\begin{align*}P_{cr} = \frac{9\pi^2EI}{L^2}\end{align*}$ $\begin{align*}P_{cr} = \frac{9\pi^2EI}{L^2}\end{align*}$ $\begin{align*}P_{cr} = \frac{9\pi^2EI}{L^2}\end{align*}$ $\begin{align*}P_{cr} = \frac{9\pi^2EI}{L^2}\end{align*}$ $\begin{align*}P_{cr} = \frac{9\pi^2EI}{L^2}\end{align*}$

Forma abrochada

$\begin{align*}v(x) = C_1\sin\left(\frac{\pi x}{L}\right)\end{align*}$

$\begin{align*}v(x) = C_1\sin\left(\frac{2\pi x}{L}\right)\end{align*}$

$\Nin{align*}v(x) = C_1\Nsin{align*}(\Nfrac{3\pi x}{L}{align*})\Nfinal{align*}$

📌 Para cualquier modo dado, $P_{cr}$ representa el límite superior práctico de la carga axial. Las imperfecciones naturales, por ejemplo, un pilar «fuera de plomo» o una mala alineación de la carga, inducirán casi con toda seguridad el pandeo cuando se supere la carga crítica.

3.0 Pilares con otras condiciones de apoyo

Hasta ahora hemos visto el comportamiento de un pilar clavado en ambos extremos. Este es el punto de partida típico. Pero se puede seguir el mismo proceso para determinar las ecuaciones correspondientes para columnas con diferentes tipos de condiciones de apoyo. En los vídeos siguientes, realizaré las derivaciones para demostrar el proceso para:

Pilares con una base fijada contra el giro y libre en la parte superior (fijo-libre)
Pilares fijados contra el giro en ambos extremos (fijo-fijo)
Pilares fijados contra el giro en la base y clavados en la parte superior (fijo-clavado)

Ecuación de pandeo para pilares restringidos contra la rotación en ambos extremos (fijo-fijo)

Ecuación de pandeo para pilares restringidos contra la rotación en la base y libres en la parte superior (fijo-libre)

Ecuación de pandeo para columnas restringidas contra la rotación en la parte inferior y fijadas en la parte superior (fijo-fijado)

Resumen de la condición de soporte

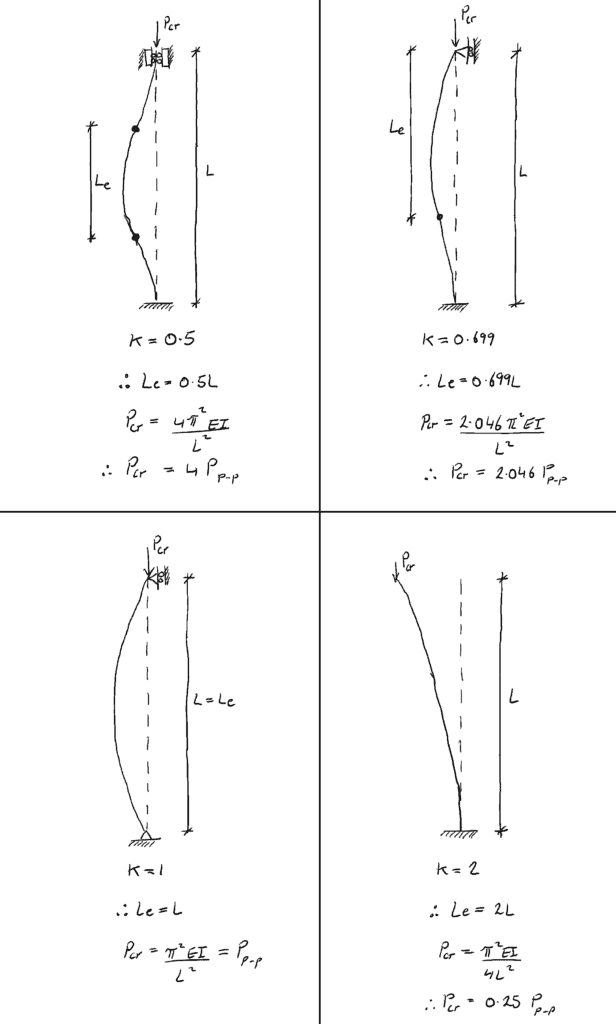
4.0 Eje de pandeo

Recordamos de la ecuación de la carga de pandeo que es función de I, el segundo momento del área de la sección transversal:

$\begin{align*}P=\frac{n^2\pi^2EI}{L^2}{end{align*}$

Por lo tanto, para una sección transversal dada, una columna siempre se pandea alrededor del eje con el segundo momento de área más bajo, el eje «más débil». Esto supone que ambos ejes tienen igual coacción. Consideremos el caso de una sección de columna universal (UC) sometida a compresión:

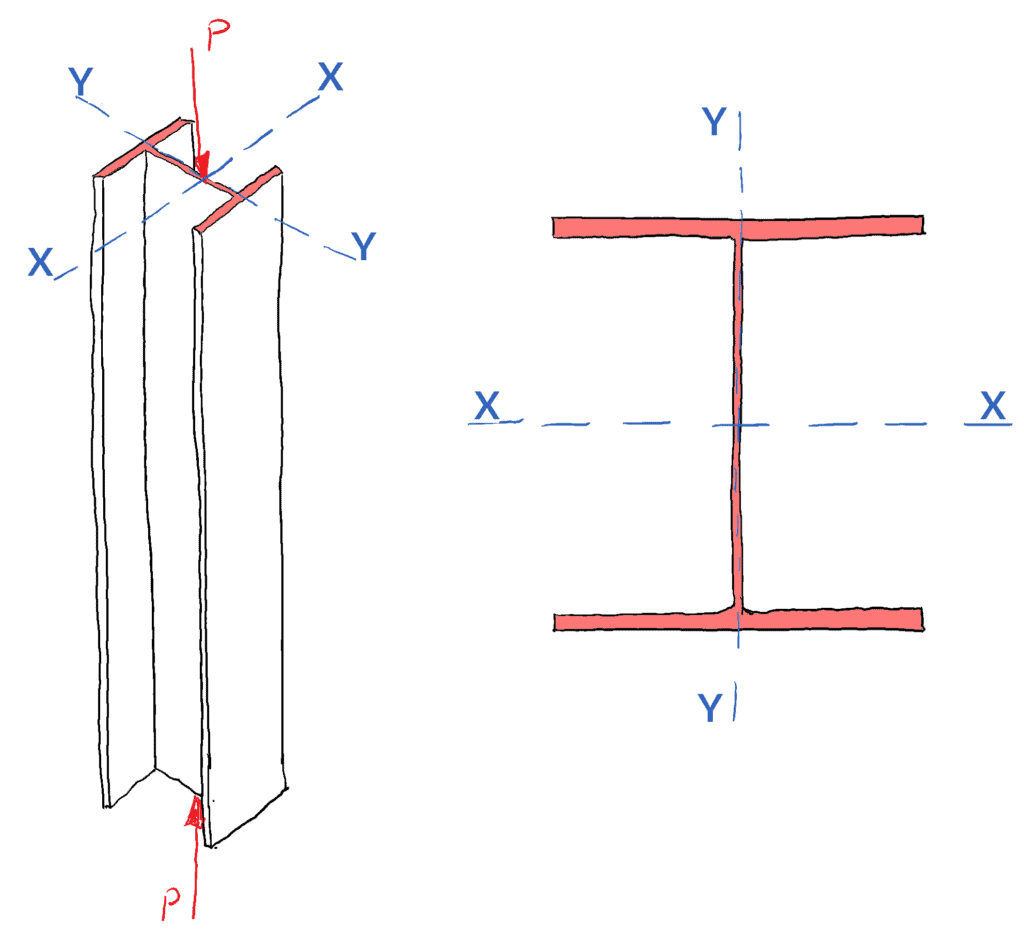
Como el eje X-X, es el eje de principio mayor (con el mayor valor del segundo momento del área -puede que lo recuerdes de tu estudio del círculo de Mohr), es el eje más fuerte y por tanto la columna se pandeará sobre el eje de principio menor o Y-Y primero.

Cuando se considera la carga de pandeo para una estructura de columna, la forma de la sección transversal juega un papel clave, debe evaluar los ejes principales mayores y menores para determinar el eje crítico para el pandeo.

5.0 Tensión crítica

📌 La tensión crítica es la tensión axial media en una sección transversalsección transversal bajo la carga crítica

${begin{align*}{sigma_{cr}={frac{P_{cr}}{A}={frac{pi^2EI}{AL^2}{end{align*}$

Ahora definimos el Radio de Giro como:

$\begin{align*}r=\sqrt{\frac{I}{A}}\end{align*}$

Por tanto, podemos escribir la tensión crítica como:

$\begin{align*}{sigma_{cr}={frac{pi^2E}{izquierda(\frac{L}{r}{derecha)^2}end{align*}$

Finalmente definimos la Relación de Esbeltez como:

$\begin{align*}\lambda=\frac{L}{r}\end{align*}$

La relación de esbeltez es una medida muy útil de la geometría de una columna y su susceptibilidad al pandeo. Una relación de esbeltez alta indica una mayor susceptibilidad al pandeo. El índice de esbeltez debe determinarse por separado para cada eje principal. Podemos intuir la relación de esbeltez visualizando ambos extremos,

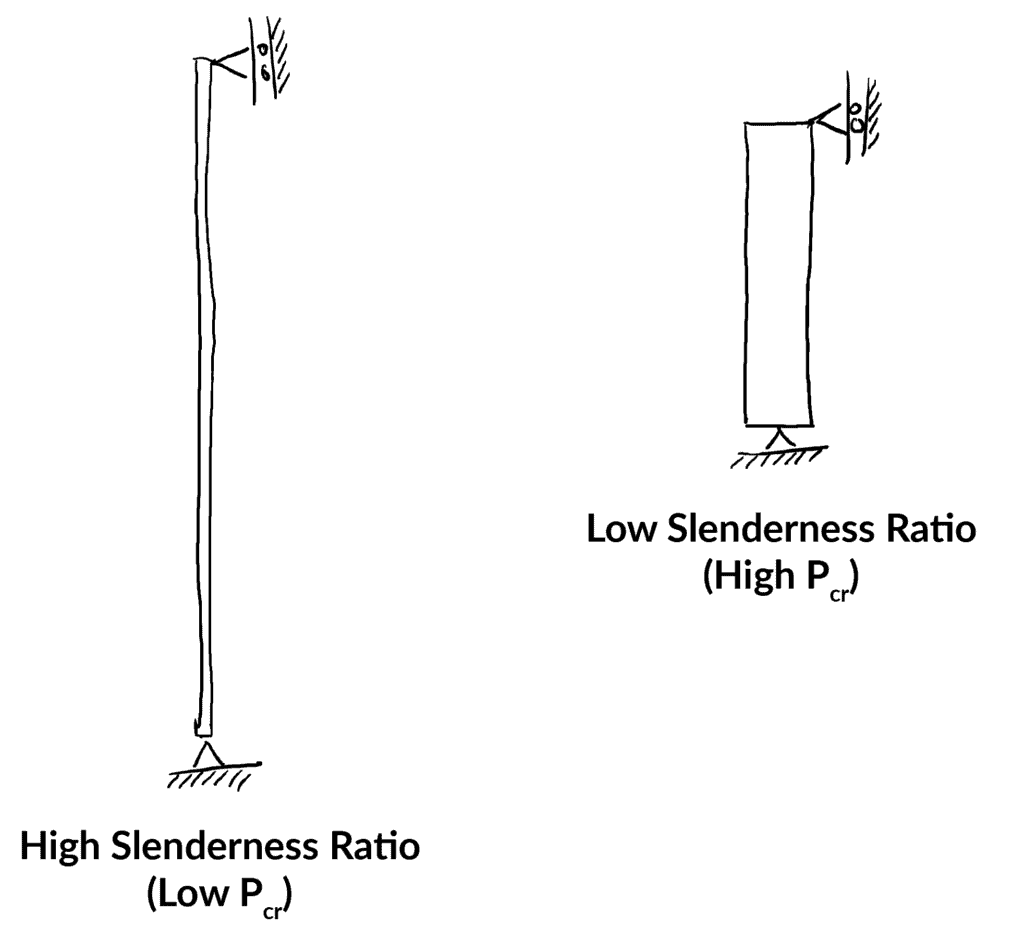
La ecuación de la tensión crítica puede, por tanto, escribirse en función de la relación de esbeltez como sigue,

$\begin{align*}\sigma_{cr}=\frac{\pi^2E}{\lambda^2}\end{align*}$

Planificando la tensión crítica en función de la relación de esbeltez para un determinado valor del módulo de Young se obtiene una Curva de Euler que muestra el rango seguro de la tensión axial media para una relación de esbeltez determinada (o el rango seguro de valores de la relación de esbeltez para una tensión axial determinada),

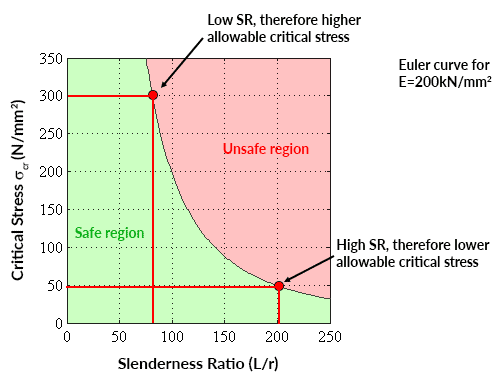
📌 Una curva de Euler sólo es válida para tensiones críticas inferiores a la tensión de fluencia del material

6.0 Longitud efectiva de la columna

El último concepto que veremos en este post es la longitud efectiva de la columna. La longitud efectiva de una columna, , es la longitud entre puntos de inflexión en la curva/forma deflectada (incluso si la forma debe extenderse hasta alcanzar un punto de inflexión – discutido más adelante). Para un pilar fijado en ambos extremos, la longitud efectiva es simplemente la longitud total del pilar entre las restricciones de los pines:

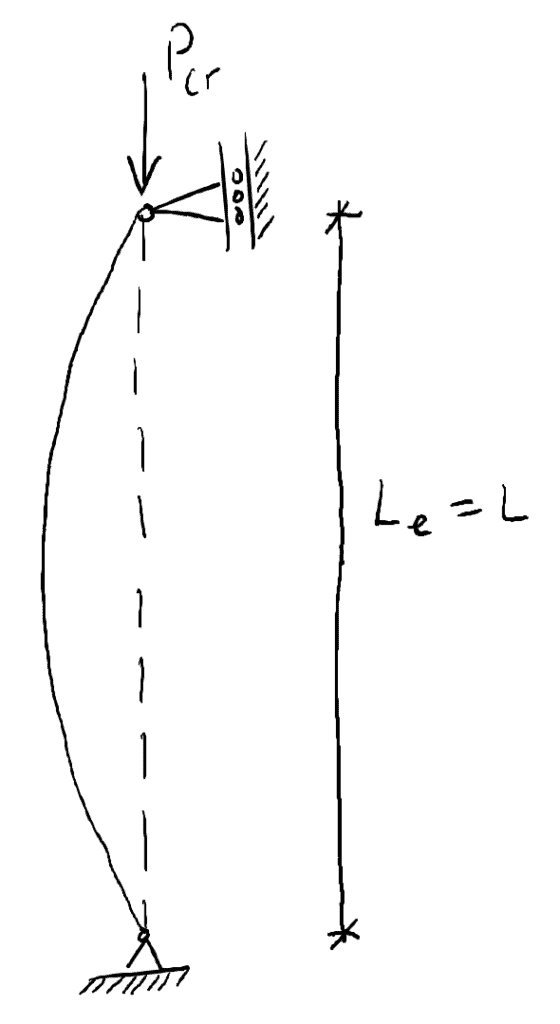
Considere un pilar con un soporte fijo en su base y sin ninguna restricción lateral en la parte superior (sin fijación). En la base no puede producirse ninguna rotación. Para obtener dos puntos de inflexión en la forma deflectada, ésta debe extenderse…

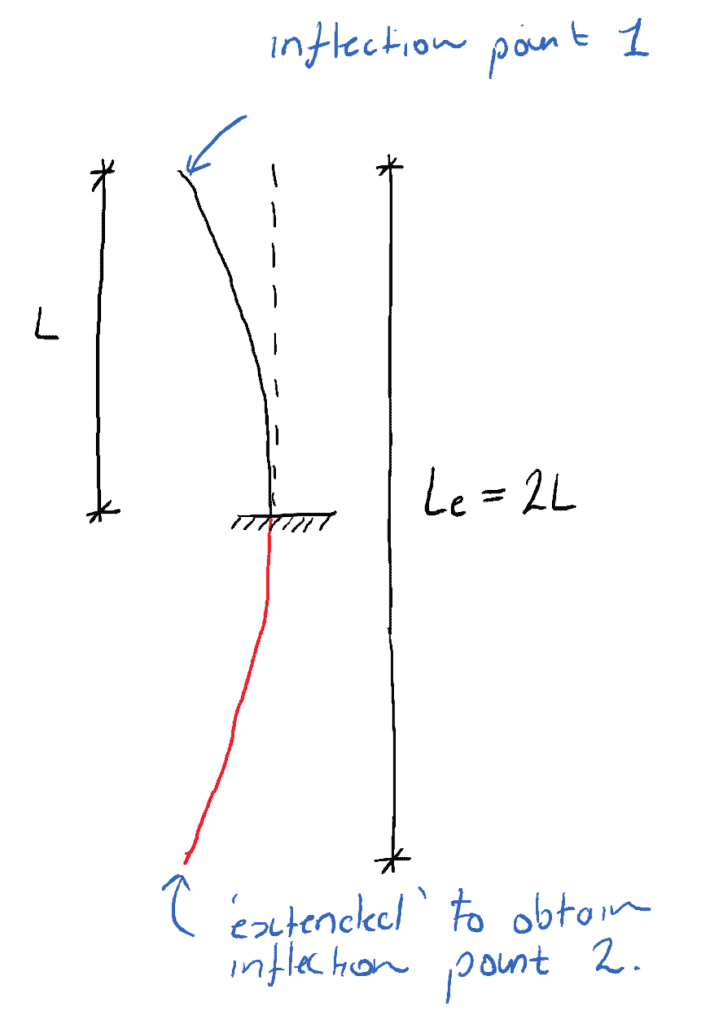
La parte roja «imaginaria» de la forma deflectada es la extensión necesaria para proporcionar el punto de inflexión número 2. Por lo tanto, la longitud efectiva para una columna libre de fijación es 2L.

📌 Otra forma de pensar en la longitud efectiva es que es la longitud de una columna de extremo fijo equivalente.

Antes de concluir nuestra discusión sobre la longitud efectiva, podemos definir una expresión general para la carga crítica como:

$\begin{align*}P_{cr}=\frac{\pi^2EI}{{L_e}^2}\end{align*}$

Si ahora introducimos el factor de longitud efectiva, , tal que , podemos plantear la carga crítica en función del factor de longitud efectiva:

$P_{align*}P_{cr}=\frac{pi^2EI}{(KL)}^2}end{align*}$

Suscríbete para recibir actualizaciones

Recibe una notificación cuando aterricen nuevos tutoriales y cursos