Factorial

¿Qué es el factorial?

El factorial (denotado o representado como n!) para un número positivo o entero (que se denota por n) es el producto de todos los números positivos que preceden o equivalen a n (el entero positivo). La función factorial se puede encontrar en varias áreas de las matemáticas, incluyendo el álgebra, el análisis matemático y la combinatoria.

A partir de los años 1200, los factoriales se utilizaron para contar permutaciones. La notación para un factorial (n!) fue introducida a principios de 1800 por Christian Kramp, un matemático francés.

La fórmula del factorial se puede ver a continuación:

Definición del Factorial

La función de un factorial se define por el producto de todos los enteros positivos anteriores y/o iguales a n, es decir:

¡n! = 1 ∙ 2 ∙ 3 ∙∙∙ (n-2) ∙ (n -1) ∙ n,

cuando se trata de valores o enteros mayores o iguales a 1. Se puede escribir entonces como:

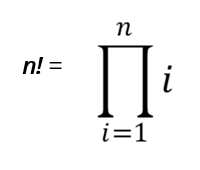
La ecuación anterior se escribe según la notación del producto pi, y da como resultado la relación recurrente que se ve a continuación:

¡N! = n ∙ (n – 1) !.

A continuación se pueden ver algunos ejemplos de la notación:

• ¡4! = 4 ∙ 3!
• ¡7! = 7 ∙ 6!
• ¡80! = 80 ∙ 79!, etc.

Tabla de factoriales

La siguiente tabla ofrece un resumen de los factoriales de los números enteros entre 0 y 10:

Factorial de 0 (Cero)

Es ampliamente conocido que el factorial de 0 es igual a 1 (uno). Se puede denotar como:

¡0! = 1

Hay varias razones que justifican la notación y definición estipuladas anteriormente. En primer lugar, la definición permite expresar de forma compacta un número considerable de fórmulas, incluida la función exponencial, y la definición crea una extensión de la relación de recurrencia a 0.

Además, cuando n = 0, la definición de su factorial (n!) abarca el producto de ningún número, lo que significa que es equivalente a la identidad multiplicativa en términos más amplios.

Además, la definición del factorial de cero incluye sólo una permutación de cero o ningún objeto. Por último, la definición también valida una serie de identidades en combinatoria.

Definiciones a tener en cuenta en relación con el factorial cero

• Combinatoria: Un área de las matemáticas que se centra en el conteo.
• Permutación: En matemáticas, la permutación se refiere a la disposición de los miembros de un conjunto en un orden o secuencia lineal.
• Relación de recurrencia: La relación de recurrencia, en matemáticas, se refiere a una ecuación que define una secuencia o un amplio conjunto de valores, de forma recursiva. Recursión significa definir algo en términos de sí mismo.

Varias aplicaciones de la función factorial

La función factorial puede encontrarse en varios campos de las matemáticas. En primer lugar, hay n! formas distinguidas de ordenar n objetos específicos en una secuencia. Además, los factoriales pueden utilizarse para dar cuenta del desconocimiento o desprecio del ordenamiento en una fórmula, sirviendo como denominador.

Los factoriales también aparecen en el álgebra a través del teorema del binomio y en el cálculo, donde aparecen en los denominadores de la fórmula de Taylor. Además, se puede encontrar un factorial en las teorías de la probabilidad y de los números y se pueden utilizar para permitir la manipulación de expresiones.

Otras secuencias similares al factorial

En matemáticas, hay una serie de secuencias que son comparables al factorial. Entre ellas se encuentran:

• Factoriales dobles, que se utilizan para simplificar integrales trigonométricas.
• Multifactoriales, que pueden denotarse con múltiples signos de exclamación.
• Primoriales, que suponen obtener el producto de los números primos, que son menores o iguales a n.
• Superfactoriales, que se definen como el producto de los n primeros factoriales.
• Hiperfactoriales, que son el resultado de multiplicar un número de valores consecutivos que van de 1 a n.

Recursos adicionales

CFI es el proveedor oficial de la certificación global de Analista de Crédito de Banca Comercial &CBCA™La acreditación de Analista de Crédito de Banca Comercial & es un estándar global para los analistas de crédito que cubre finanzas, contabilidad, análisis de crédito, análisis de flujo de caja, modelado de convenios, reembolsos de préstamos, y más. programa de certificación, diseñado para ayudar a cualquier persona a convertirse en un analista financiero de clase mundial. Para seguir avanzando en su carrera, los recursos adicionales de CFI que aparecen a continuación le serán útiles:

• Matriz de correlaciónMatriz de correlaciónUna matriz de correlación es simplemente una tabla que muestra los coeficientes de correlación para diferentes variables. La matriz representa la correlación entre todos los posibles pares de valores en una tabla. Es una poderosa herramienta para resumir un gran conjunto de datos e identificar y visualizar patrones en los datos dados.
• Matemáticas financierasMatemáticas financierasDescribe la aplicación de las matemáticas y la modelización matemática para resolver problemas financieros.A veces se denomina
• CuánticosLos analistas cuantitativos (también llamados «quants») son profesionales especializados en el diseño, desarrollo e implementación de algoritmos y modelos matemáticos o estadísticos destinados a resolver problemas financieros complejos. En su trabajo, los analistas cuantitativos aplican una mezcla de técnicas y conocimientos
• Distribución estándarDistribución muestralUna distribución muestral se refiere a una distribución de probabilidad de una estadística que proviene de la elección de muestras aleatorias de una población determinada
.