Fórmulas útiles de matemáticas para el SAT
Una de las primeras cosas que hay que hacer cuando se estudia para la sección de Matemáticas del SAT es cometer fórmulas de memoria. Si no estás seguro de por dónde empezar, esta lista te ayudará.
Aquí tienes 9 fórmulas matemáticas del SAT que te ayudarán a la hora de hacer el examen. Utiliza esta lista como inicio.
Aprende a prepararte para los exámenes estandarizados con nuestros cursos de preparación para el SAT y el ACT durante todo el año, hoy mismo.
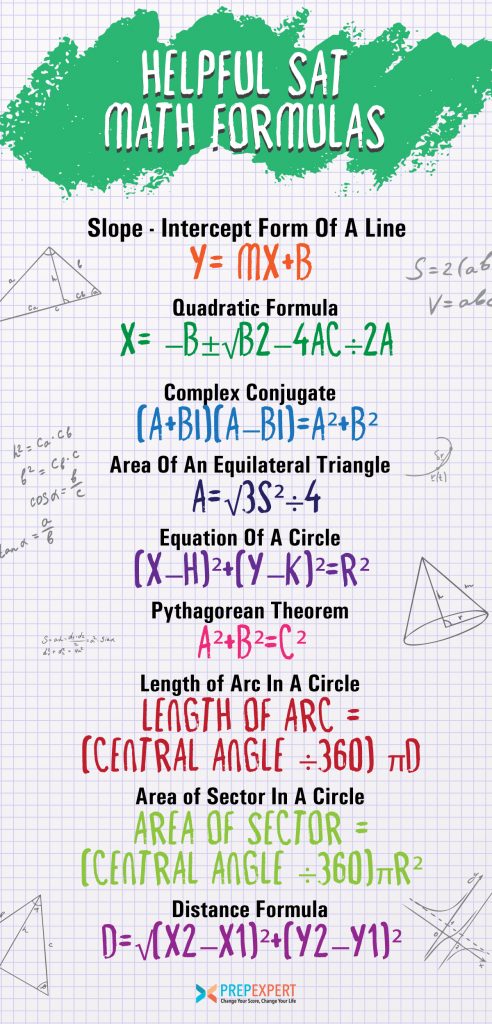
Forma de la pendiente e intersección de una recta
y=mx+b
«m» representa la pendiente de la ecuación, «b» representa el valor de la intersección y. Por ejemplo, si tenemos la ecuación y=3x+5, entonces la pendiente es ‘3’ y la intersección y es (0,5).
Fórmula cuadrática
x=-b±√b2-4ac÷2a
Con esta fórmula, puedes encontrar las raíces de una ecuación cuadrática si no es fácilmente factorizable. Sin embargo, la cuadrática tiene que tener la forma de y=ax2+bx+c.
En ese momento, introduce los coeficientes y las constantes en la fórmula. Recuerda que, debido al ± en el numerador, tendrás dos respuestas separadas.
Conjugado complejo
(a+bi)(a-bi)=a²+b²
La mayoría de los exámenes de Matemáticas del SAT tendrán, al menos, una pregunta que requiere manejar números imaginarios. La fórmula del conjugado complejo le permite cancelar la parte imaginaria de un número complejo. Como resultado, se quedará con un número real.
Área de un triángulo equilátero
A=√3s²÷4
La fórmula para el área de un triángulo regular se proporciona normalmente en la hoja de referencia del examen, pero necesita saber la altura del triángulo. A veces no se te proporcionará la altura y tendrás que averiguarla.
La buena noticia es que puedes calcular el área de un triángulo equilátero introduciendo la longitud de uno de sus lados en esta fórmula. Puede omitir el requisito de la altura!
Ecuación de un círculo
(x-h)²+(y-k)²=r²
Normalmente, una pregunta de matemáticas del SAT requerirá el uso de la ecuación de un círculo. En esta ecuación, las variables h y k representan la coordenada para el centro del círculo y r
representa el radio del círculo.
Teorema de Pitágoras
a²+b²=c²
El Teorema de Pitágoras se aplica a los triángulos rectos regulares. Su propósito es permitirte resolver una de las longitudes laterales desconocidas dada cualquier otra longitud lateral. a y b son los catetos del triángulo, y c es la hipotenusa.
Longitud de arco en un círculo
Longitud de arco = (ángulo central ÷360) πd
Las preguntas de geometría no son frecuentes en la sección de Matemáticas del SAT, pero es probable que aún recibas una pregunta sobre arcos o sectores en un círculo. Un arco es una longitud entre dos puntos de una circunferencia.
Suelen medirse extendiendo dos radios desde el centro de la circunferencia con un ángulo formado entre ellos. Puedes usar la medida de grado de ese arco como una fracción de 360 y luego multiplicarla por la ecuación de la circunferencia para encontrar la longitud del arco.
Área de sector en un círculo
Área de sector = (ángulo central ÷360)πr²
A diferencia de un arco, el sector de un círculo es el área entre dos radios que se extienden desde el centro. Visualmente, piensa en ello como una porción de pastel básicamente. De nuevo, multiplica la medida del grado como una fracción de 360 y luego multiplícala por la ecuación del área de un círculo para encontrar el área del sector.
Fórmula de la distancia
d=√(x2-x1)²+(y2-y1)²
La fórmula de la distancia es fantástica para determinar la distancia entre dos puntos rápidamente. ¡Para usarla, simplemente toma los valores de las coordenadas y conéctalos para encontrar la distancia. y asegúrate de aplicar los cuadrados y la raíz cuadrada en el paso correcto.
Para más consejos sobre estrategia de exámenes, admisiones a la universidad y solicitud de becas, inscríbete en nuestra clase GRATUITA que está ocurriendo ahora mismo!