Hallar una función exponencial dada su gráfica – Funciones exponenciales

¿Qué son las funciones exponenciales?

Antes de entrar a tratar las funciones exponenciales y graficar las funciones exponenciales, veamos primero la fórmula general y la teoría que hay detrás de las funciones exponenciales.

A continuación se muestra una de las formas más generales de una gráfica exponencial:

La ecuación de la función exponencial para esta gráfica es y=2xy=2^xy=2x, y es la gráfica exponencial más sencilla que podemos hacer. Si te preguntas cómo sería y=1xy=1^xy=1x, aquí tienes su gráfica exponencial:

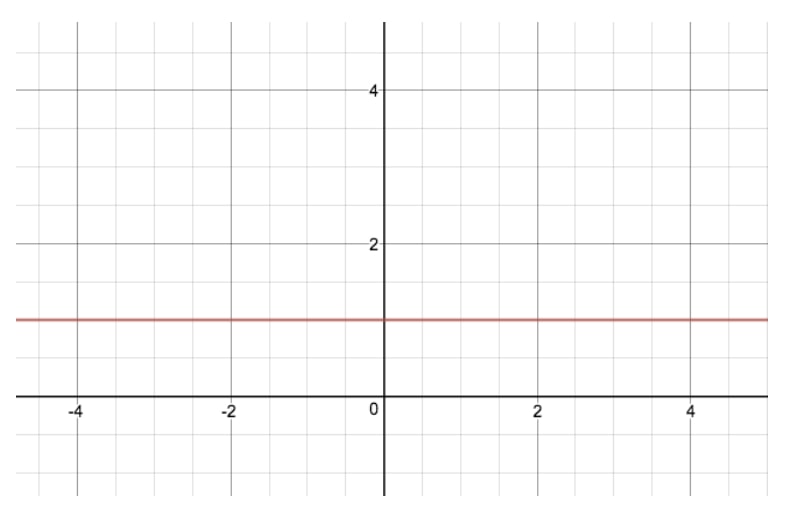
Ahora bien, en cuanto a la razón por la que las gráficas de y=2xy=2^xy=2x e y=1xy=1^xy=1x son tan diferentes, la mejor manera de entender la teoría que hay detrás de las funciones exponenciales es echar un vistazo a algunas tablas.

Encima puedes ver tres tablas para tres «valores base» diferentes – 1, 2 y 3 – todos ellos a la potencia de x. Como puedes ver, para las funciones exponenciales con un «valor base» de 1, el valor de y se mantiene constante en 1, porque 1 a la potencia de cualquier cosa es sólo 1. Por eso la gráfica anterior de y=1xy=1^xy=1x es sólo una línea recta. En cambio, en el caso de y=2xy=2^xy=2x e y=3xy=3^xy=3x (que no aparecen en la imagen), vemos una curva cada vez más pronunciada para nuestra gráfica. Esto se debe a que a medida que aumenta x, el valor de y aumenta a un valor cada vez mayor, o lo que llamamos «exponencialmente».

Ahora que tenemos una idea de cómo se ven las ecuaciones exponenciales en una gráfica, vamos a dar la fórmula general de las funciones exponenciales:

y=abd(x-c)+ky=ab^{d(x-c)}+ky=abd(x-c)+k

La fórmula anterior es un poco más complicada que las funciones anteriores con las que probablemente hayas trabajado, así que vamos a definir todas las variables.

y – el valor en el eje y

a – el factor de estiramiento o compresión vertical

b – el valor base

x – el valor en el eje x

c – el factor de traslación horizontal

d – el factor de estiramiento o compresión horizontal

k – el factor de traslación vertical

En esta lección, sólo repasaremos funciones exponenciales muy básicas, por lo que no tendrás que preocuparte por algunas de las variables anteriores. Pero, para que tengas acceso a toda la información que necesitas sobre las funciones exponenciales y cómo graficarlas, vamos a esbozar lo que el cambio de cada una de estas variables hace a la gráfica de una ecuación exponencial.

1) Variable «a»

Comparemos la gráfica de y=2xy=2^xy=2x con otra ecuación exponencial en la que modificamos «a», dándonos y=(-4)2xy=(-4)2^xy=(-4)2x

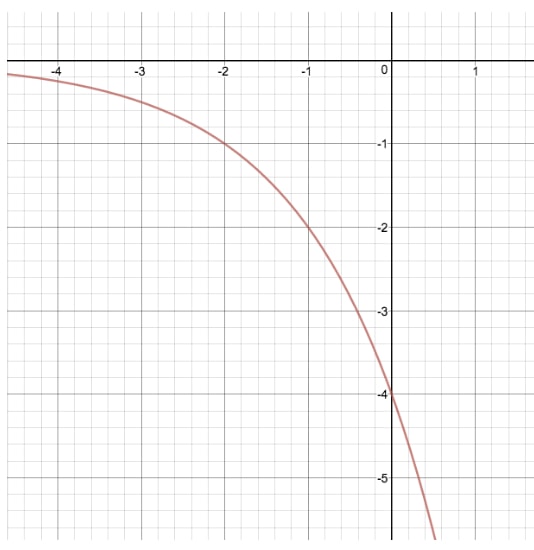
Al hacer esta transformación, hemos «estirado» y «reflejado» la gráfica original de y=2xy=2^xy=2x por sus valores y. Para encontrar «a» mirando la gráfica, lo más importante es notar que cuando x=0 y no tenemos un valor para «k», la intersección y de nuestra gráfica siempre va a ser igual a «a».

2)Variable «b»

También conocida como el «valor de la base» es simplemente el número que tiene el exponente adjunto. Encontrarlo implica el álgebra, que se discutirá más adelante en este artículo.

Variable «c»

Comparemos la gráfica de y=2xy=2^xy=2x con otra ecuación exponencial donde modificamos «c», dándonos y=2(x-2)y=2^{(x-2)}y=2(x-2)

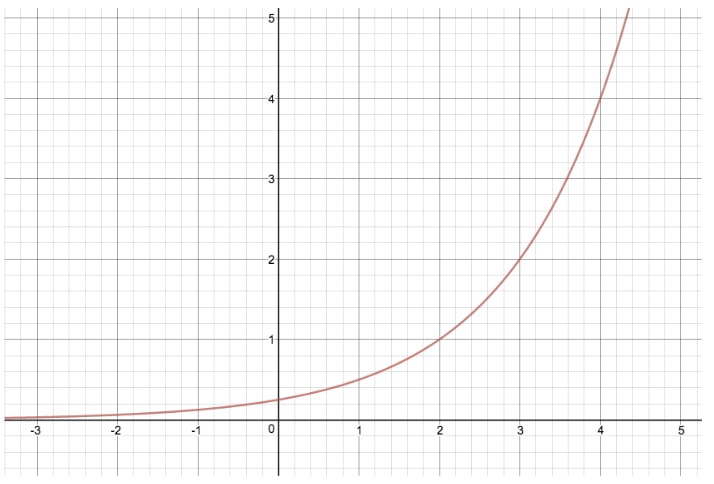
Al hacer esta transformación, hemos desplazado toda la gráfica hacia la derecha dos unidades. Si «c» fuera igual a -2, habríamos desplazado toda la gráfica hacia la izquierda dos unidades.

Variable «d»

Comparemos la gráfica de y=2xy=2^xy=2x con otra ecuación exponencial en la que modificamos «d», dándonos y=24xy=2^{4x}y=24x

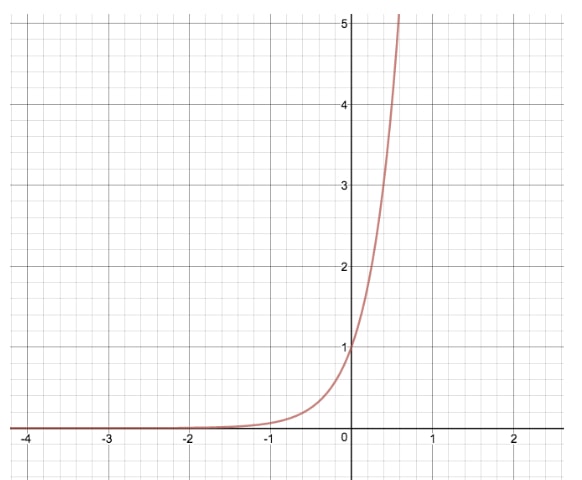
Al hacer esta transformación, hemos estirado la gráfica original de y=2xy=2^xy=2x por sus valores x, de forma similar a como la variable «a» modifica la función por sus valores y. Si «d» fuera negativa en este ejemplo, la función exponencial sufriría una reflexión horizontal en contraposición a la reflexión vertical vista con «a».

Variable «k»

Comparemos la gráfica de y=2xy=2^xy=2x con otra ecuación exponencial en la que modificamos «k», dándonos y=2x+2y=2^x+2y=2x+2

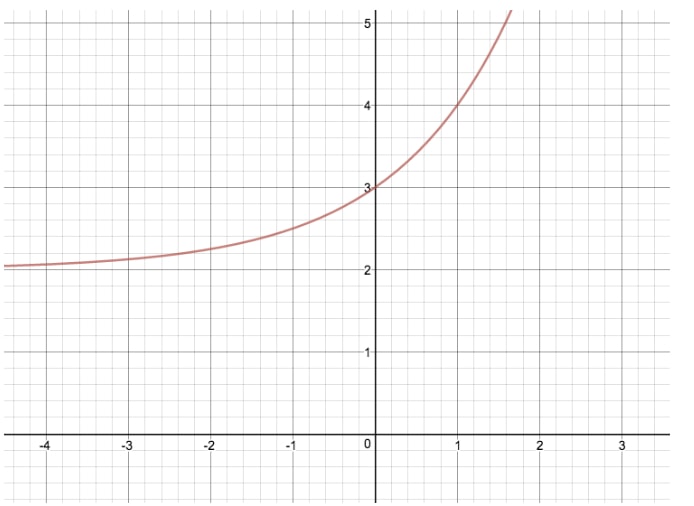
Al hacer esta transformación, hemos trasladado la gráfica original de y=2xy=2^xy=2x hacia arriba dos unidades. Si «k» fuera negativo en este ejemplo, la función exponencial se habría trasladado dos unidades hacia abajo. «k» es una variable particularmente importante, ya que también es igual a lo que llamamos la asíntota horizontal. Una asíntota es un valor de x o de y al que se aproxima una función, pero que nunca llega a igualar.

Tomemos por ejemplo la función y=2xy=2^xy=2x: para esta función exponencial, k=0, y por tanto la «asíntota horizontal» es igual a 0. Esto tiene sentido, porque no importa el valor que pongamos para x, nunca conseguiremos que y sea igual a 0. Para nuestra otra función y=2x+2y=2^x+2y=2x+2, k=2, y por tanto la asíntota horizontal es igual a 2. No hay ningún valor de x que podamos utilizar para que y=2.

¡Y esas son todas las variables! De nuevo, varias de ellas son más complicadas que otras, por lo que nos llevará tiempo acostumbrarnos a trabajar con todas ellas y sentirnos cómodos encontrándolas. Para conocer mejor las funciones exponenciales y familiarizarte con la ecuación general anterior, visita este excelente sitio web de calculadoras gráficas aquí. Tómate tu tiempo para jugar con las variables, y conseguir una mejor sensación de cómo el cambio de cada una de las variables afecta a la naturaleza de la función.

Ahora, vamos a ir al grano. Dada la gráfica de una función exponencial, ¿cómo podemos hallar la ecuación exponencial?

Cómo hallar funciones exponenciales

Hallar la ecuación de las funciones exponenciales suele ser un proceso de varios pasos, y cada problema es diferente en función de la información y el tipo de gráfica que se nos da. Dada la gráfica de las funciones exponenciales, tenemos que ser capaces de tomar alguna información de la propia gráfica, y luego resolver las cosas que no podemos tomar directamente de la gráfica. A continuación se muestra una lista de todas las variables que podemos tener que buscar, y cómo encontrarlas normalmente:

a – resuélvela usando el álgebra, o estará dada

b – resuélvela usando el álgebra, o estará dada

c – deja que x = 0 e imagina que «c» no está ahí, el valor de y será igual a la intersección y; ahora cuenta cuántas unidades tiene el valor de y para la intersección y desde el eje y, y esto será igual a «c»

d – resuélvelo usando el álgebra

k – igual al valor de la asíntota horizontal

Por supuesto, estos son sólo los pasos generales que necesitas para encontrar la ecuación de la función exponencial. La mejor manera de aprender a hacerlo es intentar algunos problemas de práctica!

Ejemplos de funciones exponenciales:

Ahora vamos a intentar un par de ejemplos para poner en práctica toda la teoría que hemos cubierto. Con la práctica, serás capaz de encontrar funciones exponenciales con facilidad!

Ejemplo 1:

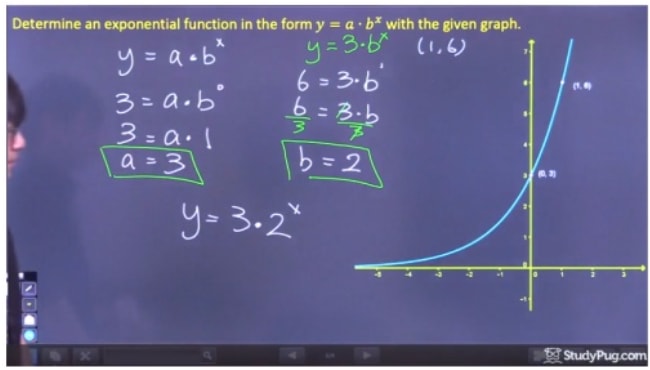
Determina la función exponencial de la forma y=abxy=ab^xy=abx de la gráfica dada.

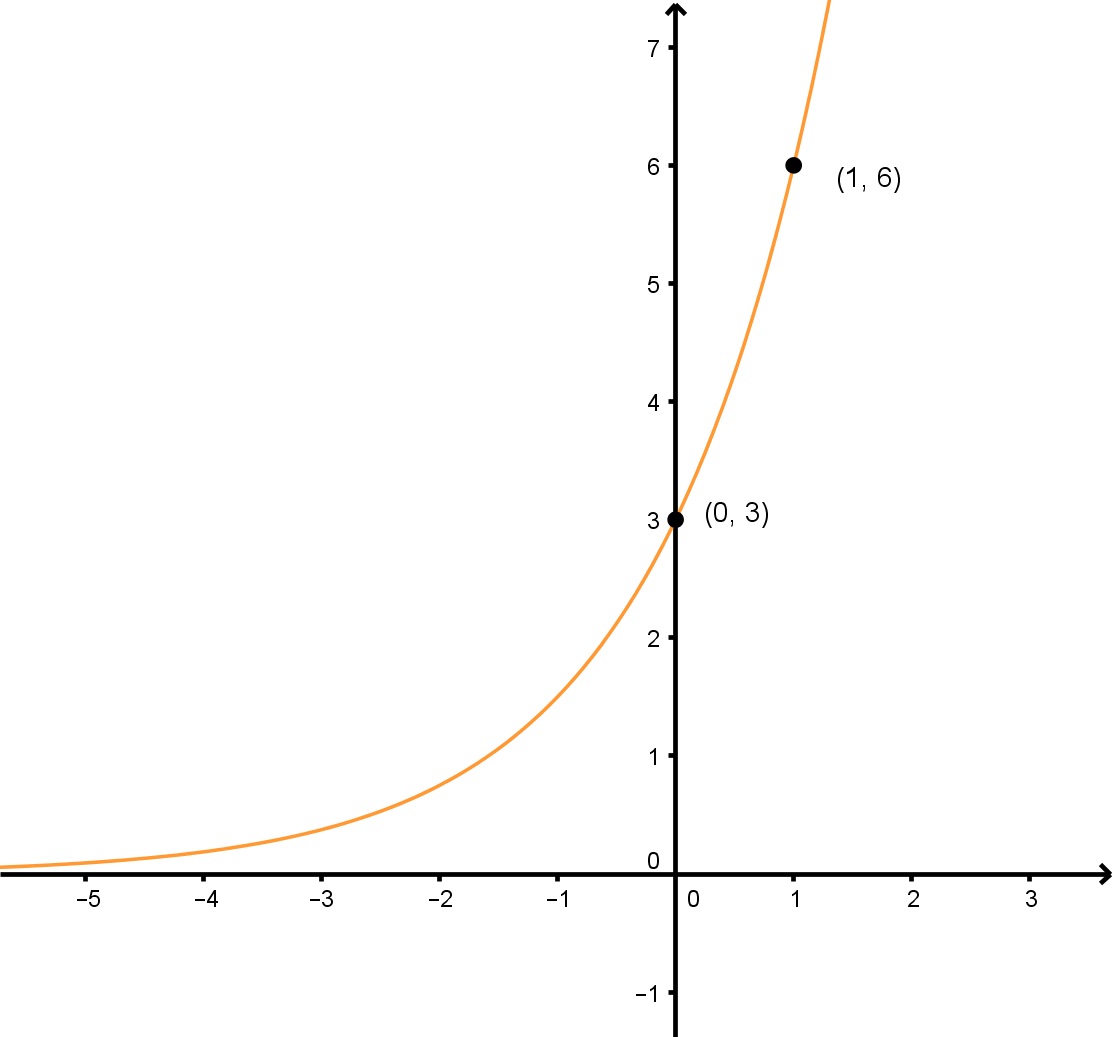
Para resolver este problema, vamos a necesitar encontrar las variables «a» y «b». Además, vamos a tener que resolver ambas algebraicamente, ya que no podemos determinarlas a partir de la propia gráfica de la función exponencial.

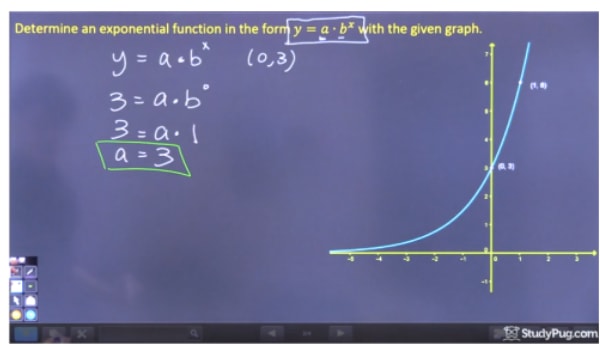
Paso 1: Resolver para «a»

Para resolver para «a», debemos elegir un punto de la gráfica en el que podamos eliminar bx porque aún no conocemos «b», y por tanto debemos elegir la intersección y (0,3). Como b0 es igual a 1, podemos encontrar que a=3. Como atajo, ya que no’ tenemos un valor para k, a es simplemente igual a la intersección y de esta ecuación.

Paso 2: Resolver para «b»

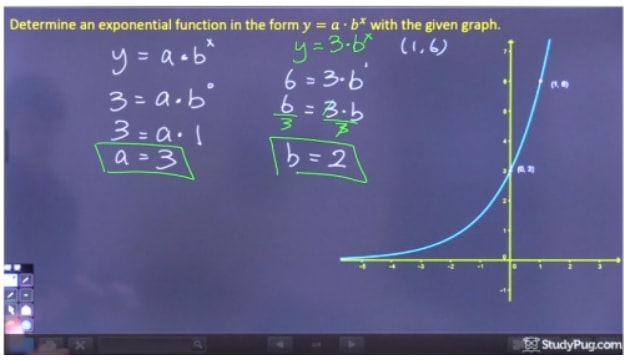
Paso 3: Escribe la ecuación final

Ejemplo 2:

Determina la función exponencial de la forma y=a2dx+ky=a2^{dx}+ky=a2dx+k de la gráfica dada.

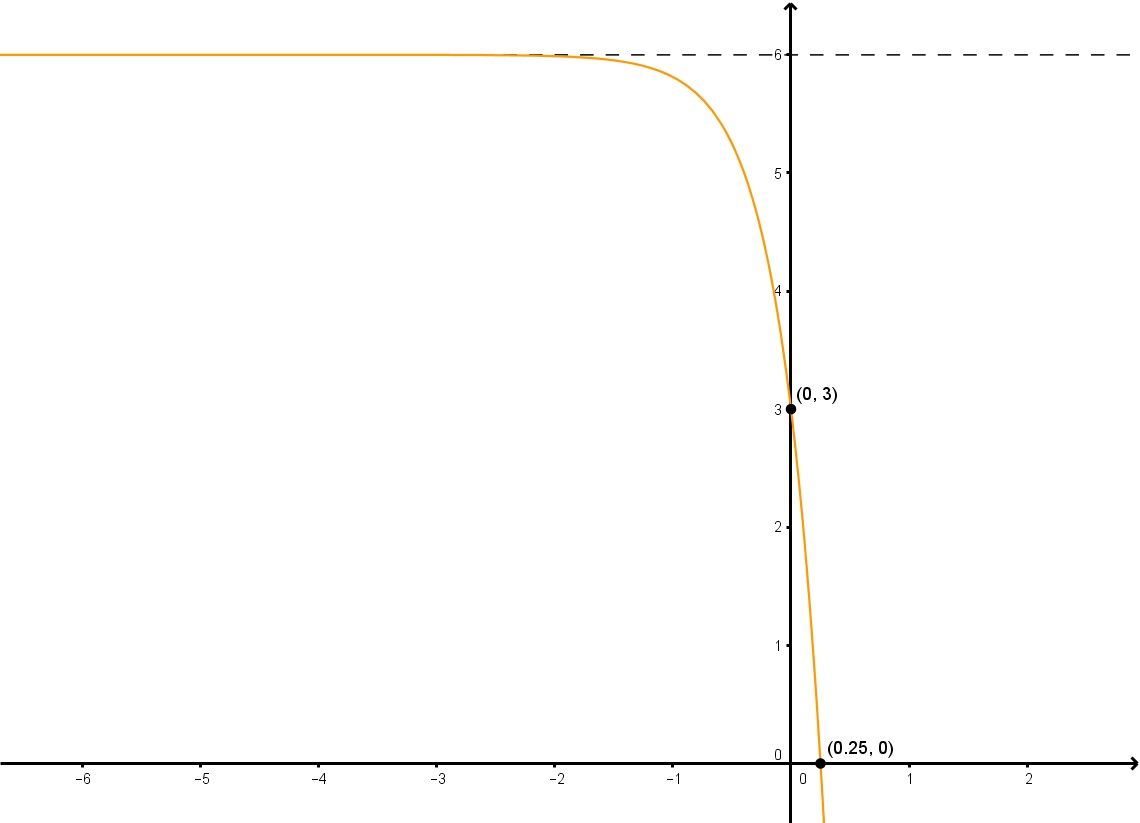
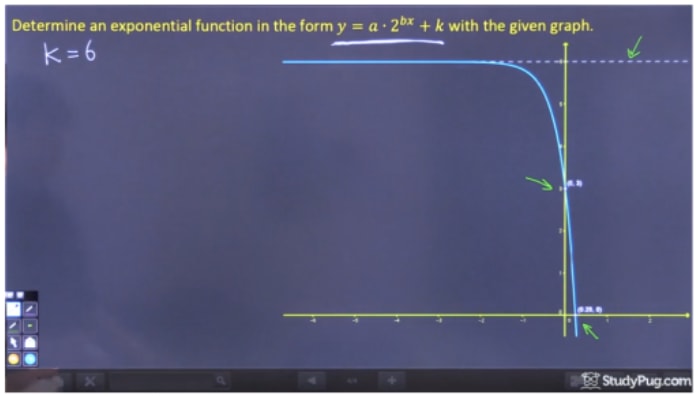
Paso 1: Encontrar «k» a partir de la gráfica

Para encontrar «k», lo único que tenemos que hacer es encontrar la asíntota horizontal, que es claramente y=6. Por lo tanto, k=6.

Paso 2: Resolver para «a»

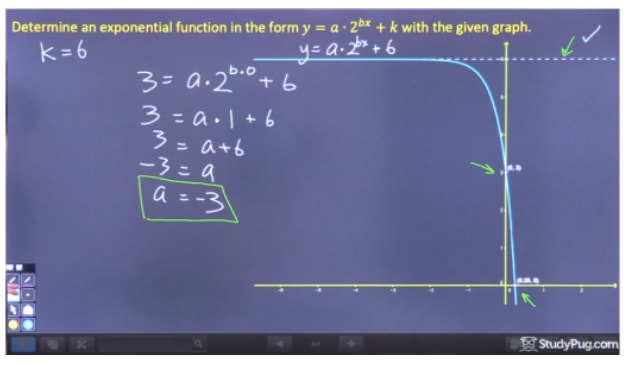
Paso 3: Resuelve «b»

Paso 4: Escribe la ecuación final

¡Y eso es todo para las funciones exponenciales! De nuevo, estas funciones son un poco más complejas que las ecuaciones de las rectas o las parábolas, así que asegúrate de hacer muchos problemas de práctica para hacerte con las nuevas variables y técnicas. Con más práctica, pronto las ecuaciones exponenciales y las gráficas de las funciones exponenciales no serán ningún problema!