Inversión de matrices: Hallar la inversa de una matriz

Vuelve al índice de lecciones | Haz las lecciones en orden | Página para imprimir

Inversión de matrices:
Hallar la inversa de una matriz (página 1 de 2)

Para las matrices, no existe la división. Puedes sumar, restar y multiplicar matrices, pero no puedes dividirlas. Sin embargo, hay un concepto relacionado, que se llama «inversión». Primero hablaré de por qué es útil la inversión, y luego te mostraré cómo hacerla.

Piensa en cuando aprendiste por primera vez a resolver ecuaciones lineales. Si te dieran algo como «3x = 6», lo resolverías dividiendo ambos lados por 3. Como multiplicar por1/3 es lo mismo que dividir por 3, también podrías multiplicar ambos lados por 1/3 para obtener la misma respuesta: x = 2. Si necesitaras resolver algo como «(3/2)x = 6», todavía podrías dividir ambos lados por 3/2, pero probablemente fuera más fácil multiplicar ambos lados por 2/3. La fracción recíproca 2/3 es la inversa de 3/2 porque, si se multiplican las dos fracciones, se obtiene 1, lo que, en este contexto, se llama «la identidad (multiplicativa)»: 1 se llama la identidad porque multiplicar algo por 1 no cambia su valor.

Aviso

Esta terminología y estos hechos son muy importantes para las matrices. Si te dan una ecuación matricial como AX = C, en la que te dan A y C y te dicen que tienes que calcular X, te gustaría «dividir» la matriz A. Pero no se puede hacer la división con matrices. Por otro lado, ¿qué pasaría si pudieras encontrar la inversa de A, algo similar a encontrar la fracción recíproca anterior? La inversa de A, que se escribe como «A-1» y se pronuncia «A inversa», te permitiría cancelar la A de la ecuación matricial y luego resolver X.

AX = C
A-1AX = A-1C
IX = A-1C
X = A-1C

¿Cómo se convirtió «A-1AX» en el lado izquierdo de la ecuación en «X»? Piensa en la naturaleza de los inversos de los números regulares. Si tienes un número (como 3/2) y su inverso (en este caso, 2/3) y los multiplicas, obtienes 1. Y el 1 es la identidad, así llamada porque 1x = x para cualquier número x. Lo mismo ocurre con las matrices. Si multiplicas una matriz (como A) y su inversa (en este caso,
A-1), obtienes la matriz identidad I. Y el sentido de la matriz identidad es que IX = X para cualquier matriz X (es decir, «cualquier matriz del tamaño correcto», por supuesto).

Hay que tener en cuenta que el orden en la multiplicación anterior es importante y no es en absoluto arbitrario. Recordemos que, para las matrices, la multiplicación no es conmutativa. Es decir, AB casi nunca es igual a BA. Así que multiplicar la ecuación matricial «por la izquierda» (para obtener A-1AX) no es en absoluto lo mismo que multiplicar «por la derecha» (para obtener AXA-1). Y no puedes decir que el producto AXA-1 es igual a A-1AX, porque no puedes cambiar el orden en la multiplicación. En cambio, tienes que multiplicar A-1 por la izquierda, poniéndolo justo al lado de la A en la ecuación matricial original. Y como tienes que hacer lo mismo a ambos lados de una ecuación cuando estás resolviendo, debes multiplicar «por la izquierda» en el lado derecho de la ecuación también, lo que resulta en A-1C. No puedes ser casual con tu colocación de las matrices; debes ser preciso, correcto y consistente. Esta es la única manera de cancelar con éxito A y resolver la ecuación matricial.

Como has visto anteriormente, las matrices inversas pueden ser muy útiles para resolver ecuaciones matriciales. Pero, dada una matriz, ¿cómo se invierte? Cómo se encuentra la inversa? La técnica para invertir matrices es bastante ingeniosa. Para una matriz dada A y su inversa A-1, sabemos que tenemos A-1A = I. Vamos a utilizar la matriz identidad I en el proceso para invertir una matriz.

Halla la inversa de la siguiente matriz.

Primero, escribo las entradas la matriz A, pero las escribo en una matriz de doble ancho:

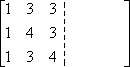
Matriz de 3 × 6 con la mitad derecha vacía

En la otra mitad de doble ancho, escribo la matriz identidad:

Ahora haré operaciones matriciales de fila para convertir el lado izquierdo del doble ancho en la identidad. (Como siempre con las operaciones de fila, no hay una forma «correcta» de hacer esto. Lo que sigue son sólo los pasos que se me ocurrieron a mí. Tus cálculos podrían ser fácilmente muy diferentes.)

Operaciones de fila de matrices

Ahora que el lado izquierdo del doble ancho contiene la identidad, el lado derecho contiene la inversa. Es decir, la matriz inversa es la siguiente:

multiplicación de matrices que da como resultado la identidad

Tenga en cuenta que, en la «vida real», la inversa rara vez es una matriz llena de bonitos números enteros como esta. Sin embargo, con un poco de suerte, sobre todo si haces las inversas a mano, te darán unas tan bonitas como esta para que las hagas.

Top | 1 | 2 | Volver al índice siguiente >>

Cite este artículo como:

Stapel, Elizabeth. «Inversión de la matriz: Encontrar la inversa de una matriz». Purplemath. Disponible en
https://www.purplemath.com/modules/mtrxinvr.htm. Accessed

2016

Dejar una respuesta Cancelar la respuesta