La media de oro: ¿un gran descubrimiento o un fenómeno natural?

¿Qué tienen en común las fachadas de la National Gallery de Trafalgar Square, en Londres, y la Ópera de Sídney, en Australia?

La mayoría de la gente sugeriría que los dos edificios tienen pocas similitudes: el primero es simétrico y de proporciones clásicas, mientras que el segundo es moderno, orgánico y curvilíneo.

Un arquitecto podría ofrecer la provocativa respuesta de que ambos edificios presentan composiciones de formas geométricas, combinando círculos, cuadrados y rectángulos. Pero esta respuesta no es la razón por la que ambos están vinculados en la cultura popular.

En cambio, se pueden encontrar en las listas de edificios que supuestamente se basan en la media áurea, descrita a continuación, para lograr una composición estética perfecta.

La media áurea -también conocida como la sección áurea o la divina proporción- es un concepto matemático que se suele remontar al siglo XV, un período en el que la geometría servía tanto para fines prácticos como simbólicos.

Es una proporción que define una relación recurrente entre un elemento mayor y un subconjunto menor de ese elemento.

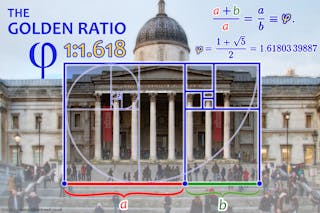
En términos matemáticos sencillos, si una línea ab está dividida por un punto C, de tal manera que la relación entre la línea entera (AB) y el segmento más largo (AC) es igual a la relación entre el segmento más largo (AC) y el segmento más pequeño (CB), entonces la relación AB : AC (y, por supuesto, la relación del subconjunto AC : CB) se conoce como la media áurea (φ o «phi»).

Así, por ejemplo, si la longitud de la línea de partida AB es 1,000, entonces la Media de Oro es aproximadamente 1,618.

Cuando la Media de Oro se conceptualiza en dos dimensiones se presenta típicamente como una espiral regular que se define por una serie de cuadrados y arcos, cada uno de los cuales forma «Rectángulos de Oro».

Utilizada por los antiguos arquitectos

Hay pruebas de que los antiguos arquitectos egipcios, romanos y griegos eran capaces de producir esta proporción utilizando herramientas sencillas y, al igual que sus homólogos del siglo XV, pueden haberla considerado con un mayor significado figurativo.

Este potencial simbólico surge debido a la manera en que la forma de espiral de la media se asemeja a los patrones de crecimiento observados en la naturaleza y sus proporciones recuerdan a las del cuerpo humano. Así, estas espirales y rectángulos sencillos, que servían para sugerir la presencia de un orden universal subyacente al mundo, fueron denominados «dorados» o «divinos».

Para el arquitecto antiguo, el Rectángulo Dorado debía ofrecer una receta para crear edificios fáciles de dibujar, agradables a la vista y, lo que es más importante, que pudieran justificarse sobre la base de que representaban una conexión con Dios o el universo.

En una época en la que, para el arquitecto, la decapitación era un riesgo más común que los litigios, la Sección Áurea ofrecía un tipo especial de indemnización.

Sin embargo, mientras que la mayoría de los símbolos del mundo antiguo han perdido ahora su poder, la Proporción Aurea sigue disfrutando de un culto, con muchos cientos de sitios web que muestran su forma espiral superpuesta a girasoles, conchas, pinturas famosas y los rostros de actores populares. El culto contemporáneo a la media de oro presenta estas superposiciones como prueba del secreto oculto del universo.

El problema de estas afirmaciones es que los investigadores han demostrado repetidamente que la Proporción Áurea no es una proporción universalmente atractiva y que no es estadísticamente significativa en la naturaleza o en el cuerpo humano. Pero el hecho de que sus propiedades más místicas hayan sido ampliamente refutadas no debería servir para relegar esta teoría a la categoría de esotérica.

Geometría natural

Como todas las proporciones estéticas (el «Modulor» de Le Corbusier y el «Número Plástico» de van der Laan son igualmente dignos), su amplia aplicación en el diseño proporciona un grado de orden y consistencia a una obra, algo importante en arquitectura porque un edificio rara vez se experimenta desde una única distancia.

Utilizando cualquiera de estas proporciones, un arquitecto puede diseñar un picaporte que tenga una relación complementaria con su puerta, que a su vez tenga una relación similar con su muro de cerramiento, y así sucesivamente. Los sistemas proporcionales son útiles para este fin, pero su presencia, incluso en un gran edificio, no debe considerarse especialmente significativa.

En la década de 1980, se llevaron a cabo experimentos en los que se entregaron a los niños reglas y pares de compases y se les animó a dibujar formas. No pasó mucho tiempo antes de que se produjeran los primeros círculos y cuadrados, luego triángulos, cuadrículas y arcos, y antes de que terminara la primera hora, empezaron a aparecer los Rectángulos Dorados.

¿Implica esto que la Media Dorada está incrustada en el subconsciente de todos los niños o es simplemente una forma que surge naturalmente del uso de este conjunto particular de herramientas?

Se recordará que tanto la National Gallery como la Ópera de Sidney -mencionadas al principio de este artículo- son composiciones de rectángulos y arcos, dibujadas en ambos casos por arquitectos con una regla y un par de compases. También fueron dibujados por arquitectos (William Wilkins y Jørn Utzon, respectivamente) que conocían la tradición clásica y sus tropos geométricos.

Por ambas razones, la presencia de algo que se aproxima vagamente a la media de oro no debería considerarse un gran descubrimiento, pero podría ser una señal de que el arquitecto había sido entrenado para apreciar la necesidad de consistencia dentro de un diseño.