Finden einer Exponentialfunktion anhand ihres Graphen – Exponentialfunktionen

Was sind Exponentialfunktionen?

Bevor wir uns mit Exponentialfunktionen und dem Graphen von Exponentialfunktionen beschäftigen, wollen wir zunächst einen Blick auf die allgemeine Formel und Theorie hinter Exponentialfunktionen werfen.

Nachfolgend sehen Sie eine der allgemeinsten Formen eines Exponentialgraphen:

Die Gleichung der Exponentialfunktion zu diesem Graphen ist y=2xy=2^xy=2x, und ist der einfachste Exponentialgraph, den wir erstellen können. Wenn Sie sich fragen, wie y=1xy=1^xy=1x aussehen würde, hier ist sein Exponentialgraph:

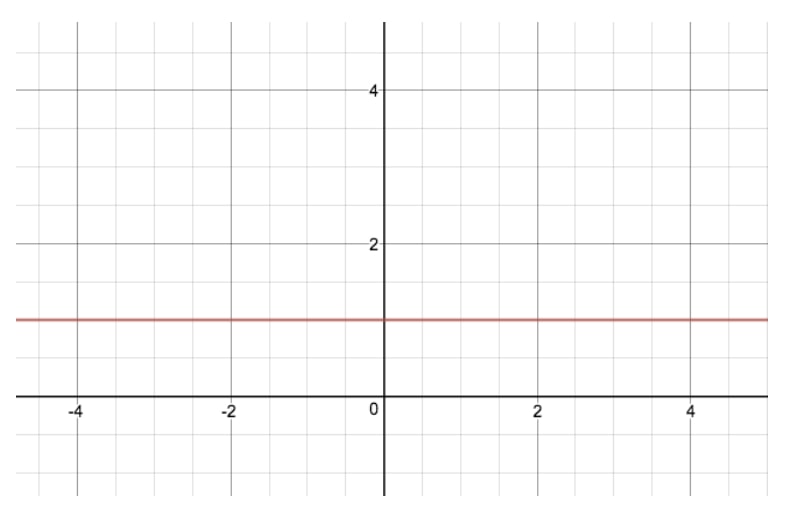
Nun, um zu verstehen, warum die Graphen von y=2xy=2^xy=2x und y=1xy=1^xy=1x so unterschiedlich sind, schaut man sich am besten einige Tabellen an, um die Theorie hinter Exponentialfunktionen zu verstehen.

Oben sehen Sie drei Tabellen für drei verschiedene „Basiswerte“ – 1, 2 und 3 -, die alle eine Potenz von x sind. Wie Sie sehen können, bleibt bei Exponentialfunktionen mit einem „Basiswert“ von 1 der Wert von y konstant bei 1, weil 1 hoch 1 einfach 1 ist. Deshalb ist der obige Graph von y=1xy=1^xy=1x einfach eine Gerade. Im Fall von y=2xy=2^xy=2x und y=3xy=3^xy=3x (nicht abgebildet) sehen wir dagegen eine zunehmend steiler werdende Kurve für unseren Graphen. Das liegt daran, dass mit steigendem x der Wert von y immer größer wird, was wir „exponentiell“ nennen.

Nun, da wir eine Vorstellung davon haben, wie Exponentialgleichungen in einem Graphen aussehen, lassen Sie uns die allgemeine Formel für Exponentialfunktionen angeben:

y=abd(x-c)+ky=ab^{d(x-c)}+ky=abd(x-c)+k

Die obige Formel ist ein wenig komplizierter als die vorherigen Funktionen, mit denen Sie wahrscheinlich gearbeitet haben, also lassen Sie uns alle Variablen definieren.

y – der Wert auf der y-Achse

a – der vertikale Streckungs- oder Stauchungsfaktor

b – der Basiswert

x – der Wert auf der x-Achse

c – der horizontale Translationsfaktor

d – der horizontale Streckungs- oder Stauchungsfaktor

k – der vertikale Translationsfaktor

In dieser Lektion werden wir nur sehr grundlegende Exponentialfunktionen durchgehen, so dass Sie sich über einige der oben genannten Variablen keine Gedanken machen müssen. Damit Sie aber alle Informationen haben, die Sie über Exponentialfunktionen und die grafische Darstellung von Exponentialfunktionen benötigen, lassen Sie uns kurz skizzieren, was die Änderung jeder dieser Variablen mit dem Graphen einer Exponentialgleichung macht.

1) Variable „a“

Lassen Sie uns den Graphen von y=2xy=2^xy=2x mit einer anderen Exponentialgleichung vergleichen, bei der wir „a“ ändern, und wir erhalten y=(-4)2xy=(-4)2^xy=(-4)2x

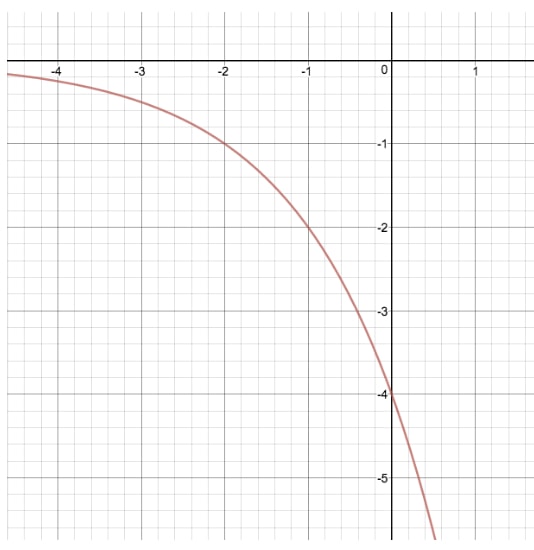
Indem wir diese Transformation durchführen, haben wir den ursprünglichen Graphen von y=2xy=2^xy=2x um seine y-Werte „gestreckt“ und „gespiegelt“. Um „a“ durch Betrachten des Graphen zu finden, ist es wichtig zu wissen, dass der y-Achsenabschnitt unseres Graphen immer gleich „a“ ist, wenn x=0 ist und wir keinen Wert für „k“ haben.

2)Variable „b“

Auch als „Basiswert“ bekannt, ist dies einfach die Zahl, an die der Exponent angehängt ist. Um ihn zu finden, ist Algebra nötig, die wir später in diesem Artikel besprechen werden.

Variable „c“

Lassen Sie uns den Graphen von y=2xy=2^xy=2x mit einer anderen Exponentialgleichung vergleichen, bei der wir „c“ ändern, und wir erhalten y=2(x-2)y=2^{(x-2)}y=2(x-2)

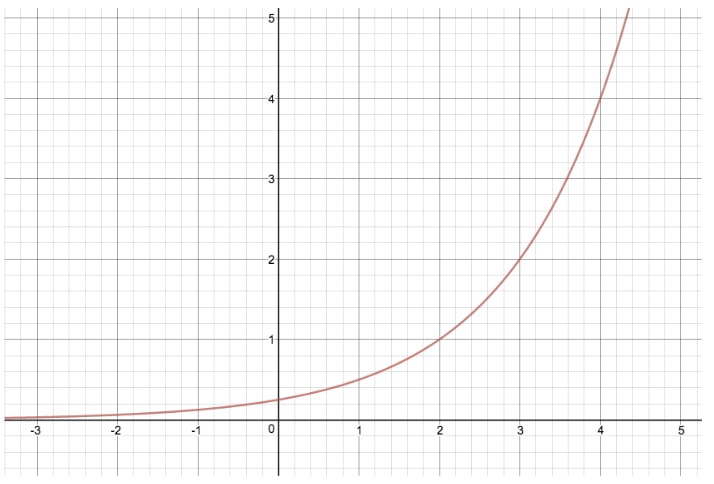
Indem wir diese Transformation durchführen, haben wir den gesamten Graphen um zwei Einheiten nach rechts verschoben. Wenn „c“ gleich -2 wäre, hätten wir den gesamten Graphen um zwei Einheiten nach links verschoben.

Variable „d“

Lassen Sie uns den Graphen von y=2xy=2^xy=2x mit einer anderen Exponentialgleichung vergleichen, bei der wir „d“ ändern, Wir erhalten y=24xy=2^{4x}y=24x

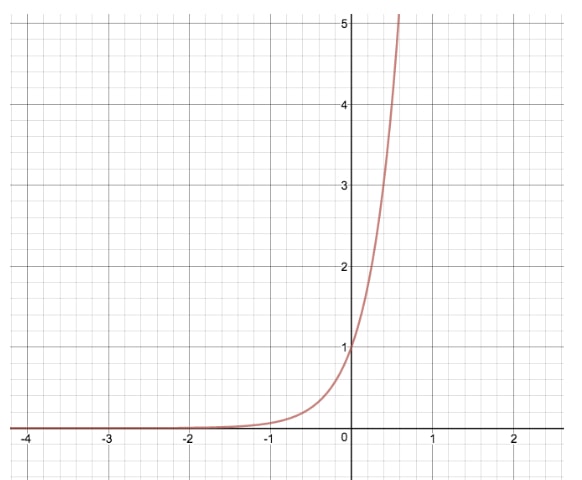
Durch diese Transformation, haben wir den ursprünglichen Graphen von y=2xy=2^xy=2x um seine x-Werte gestreckt, ähnlich wie die Variable „a“ die Funktion um ihre y-Werte modifiziert. Wäre „d“ in diesem Beispiel negativ, würde die Exponentialfunktion eine horizontale Spiegelung erfahren, im Gegensatz zur vertikalen Spiegelung mit „a“.

Variable „k“

Lassen Sie uns den Graphen von y=2xy=2^xy=2x mit einer anderen Exponentialgleichung vergleichen, bei der wir „k“ modifizieren, Wir erhalten y=2x+2y=2^x+2y=2x+2

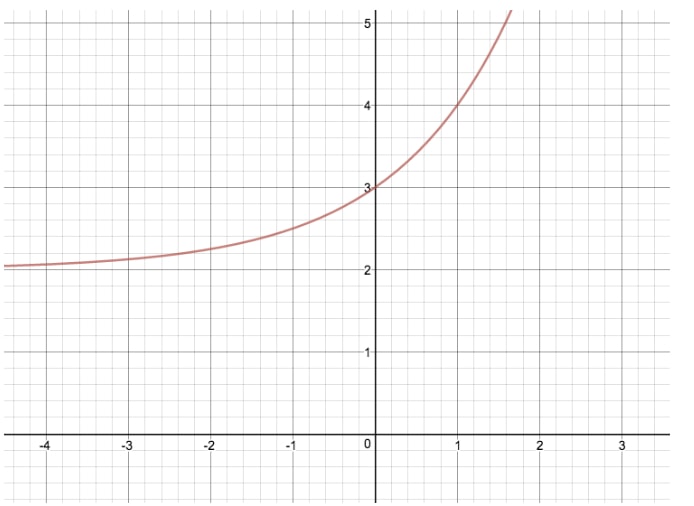
Durch diese Transformation, haben wir den ursprünglichen Graphen von y=2xy=2^xy=2x um zwei Einheiten nach oben übersetzt. Wäre „k“ in diesem Beispiel negativ, wäre die Exponentialfunktion um zwei Einheiten nach unten übersetzt worden. „k“ ist eine besonders wichtige Variable, da sie auch dem entspricht, was wir die horizontale Asymptote nennen! Eine Asymptote ist ein Wert für x oder y, dem sich eine Funktion nähert, den sie aber nie erreicht.

Nehmen wir als Beispiel die Funktion y=2xy=2^xy=2x: Für diese Exponentialfunktion ist k=0, und somit ist die „horizontale Asymptote“ gleich 0. Das macht Sinn, denn egal welchen Wert wir für x einsetzen, wir werden y nie gleich 0 bekommen. Für unsere andere Funktion y=2x+2y=2^x+2y=2x+2, ist k=2, und daher ist die horizontale Asymptote gleich 2. Es gibt keinen Wert für x, den wir verwenden können, um y=2 zu machen.

Und das sind alle Variablen! Wiederum sind einige davon komplizierter als andere, sodass es einige Zeit dauern wird, bis man sich daran gewöhnt hat, mit allen zu arbeiten und sie zu finden. Um einen besseren Einblick in Exponentialfunktionen zu bekommen und sich mit der obigen allgemeinen Gleichung vertraut zu machen, besuchen Sie diese ausgezeichnete Website für grafische Rechner hier. Nehmen Sie sich die Zeit, mit den Variablen herumzuspielen und ein besseres Gefühl dafür zu bekommen, wie sich das Ändern der einzelnen Variablen auf die Art der Funktion auswirkt.

Nun kommen wir zur Sache. Wie kann man bei einem Graphen einer Exponentialfunktion die Exponentialgleichung finden?

Wie findet man Exponentialfunktionen?

Die Gleichung von Exponentialfunktionen zu finden, ist oft ein mehrstufiger Prozess, und jedes Problem ist anders, je nach den Informationen und der Art des Graphen, die wir erhalten. Angesichts des Graphen von Exponentialfunktionen müssen wir in der Lage sein, einige Informationen aus dem Graphen selbst zu entnehmen und dann für die Dinge zu lösen, die wir nicht direkt aus dem Graphen entnehmen können. Im Folgenden finden Sie eine Liste aller Variablen, nach denen wir möglicherweise suchen müssen, und wie wir sie normalerweise finden:

a – lösen Sie es mit Hilfe der Algebra, oder es wird gegeben

b – lösen Sie es mit Hilfe der Algebra, oder es wird gegeben

c – lassen Sie x = 0 und stellen Sie sich vor, dass „c“ nicht da ist, dann ist der Wert von y gleich dem y-Achsenabschnitt; Zählen Sie nun, wie viele Einheiten der y-Wert für den y-Achsenabschnitt von der y-Achse entfernt ist, und dies wird gleich „c“ sein

d – lösen Sie ihn mit Hilfe der Algebra

k – gleich dem Wert der horizontalen Asymptote

Natürlich sind dies nur die allgemeinen Schritte, die Sie unternehmen müssen, um die Gleichung der Exponentialfunktion zu finden. Der beste Weg, dies zu lernen, ist, einige Übungsaufgaben zu lösen!

Exponentialfunktionen Beispiele:

Nun wollen wir ein paar Beispiele ausprobieren, um die ganze Theorie, die wir behandelt haben, in die Praxis umzusetzen. Mit etwas Übung werden Sie in der Lage sein, Exponentialfunktionen mit Leichtigkeit zu finden!

Beispiel 1:

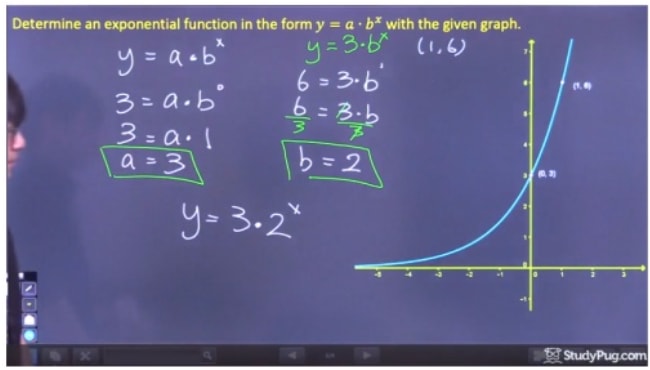
Bestimmen Sie die Exponentialfunktion in der Form y=abxy=ab^xy=abx des gegebenen Graphen.

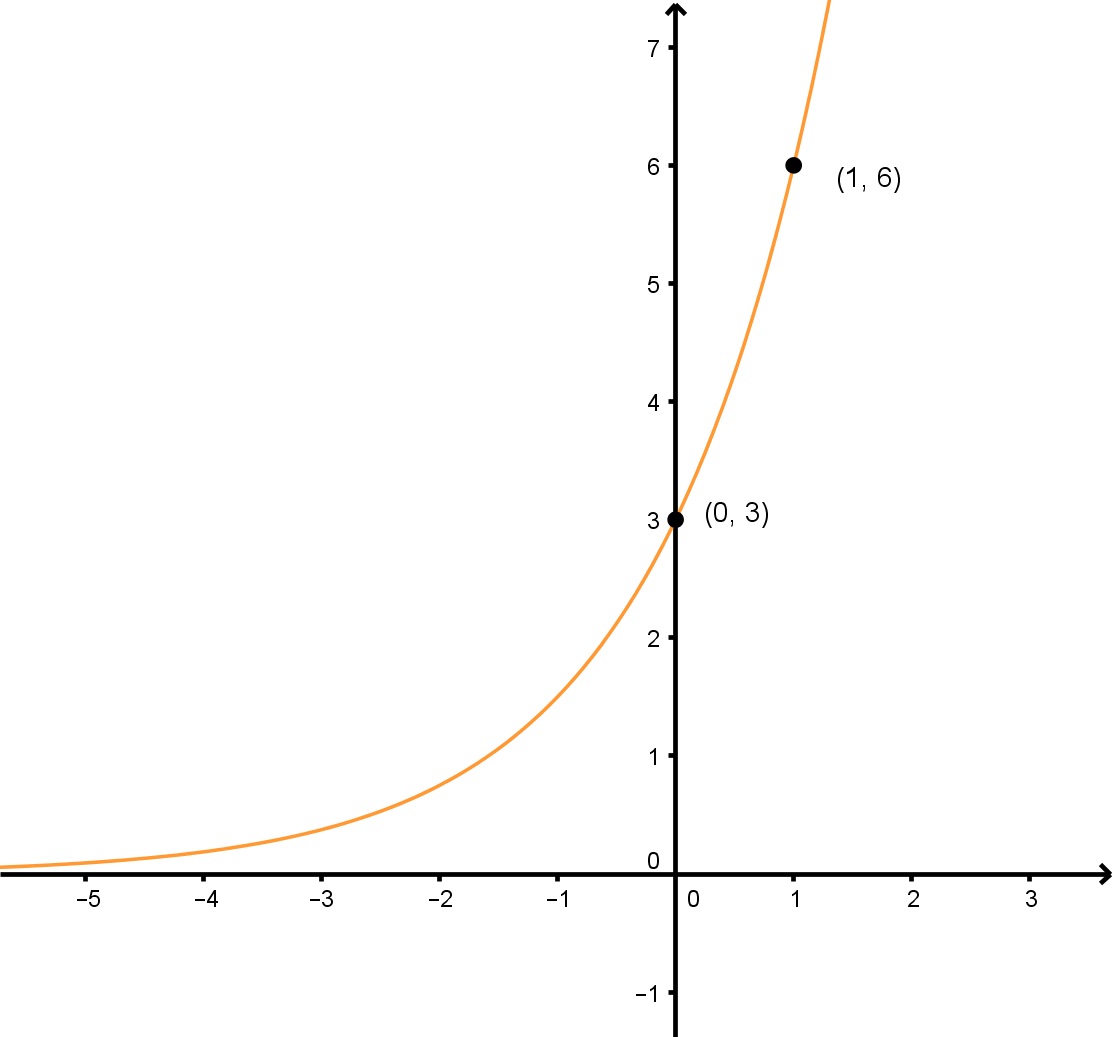
Um diese Aufgabe zu lösen, müssen wir die Variablen „a“ und „b“ finden. Außerdem müssen wir beide algebraisch lösen, da wir sie nicht aus dem Graphen der Exponentialfunktion selbst bestimmen können.

Schritt 1: Lösen für „a“

Um „a“ zu lösen, müssen wir einen Punkt auf dem Graphen wählen, an dem wir bx eliminieren können, da wir „b“ noch nicht kennen und daher den y-Achsenabschnitt (0,3) wählen sollten. Da b0 gleich 1 ist, können wir feststellen, dass a=3 ist. Als Abkürzung, da wir keinen Wert für k haben, ist a einfach gleich dem y-Achsenabschnitt dieser Gleichung.

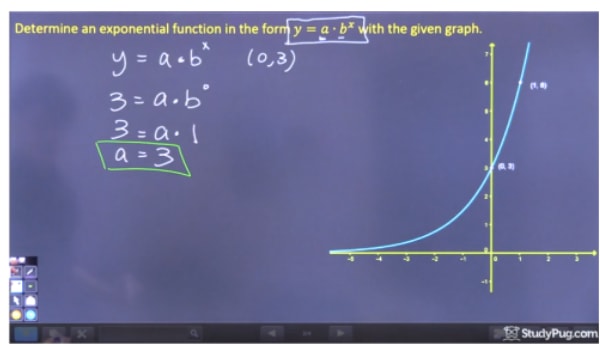
Schritt 2: Lösen Sie für „b“

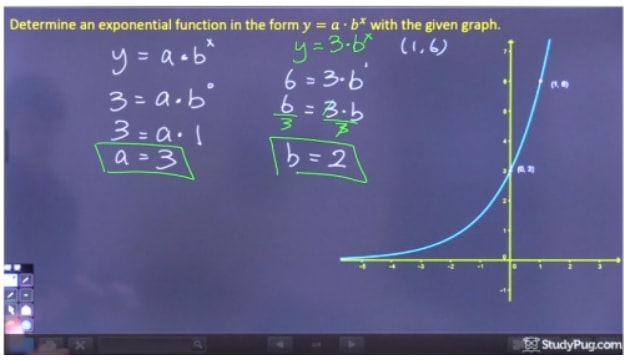
Schritt 3: Schreiben Sie die endgültige Gleichung

Beispiel 2:

Bestimmen Sie die Exponentialfunktion in der Form y=a2dx+ky=a2^{dx}+ky=a2dx+k des gegebenen Graphen.

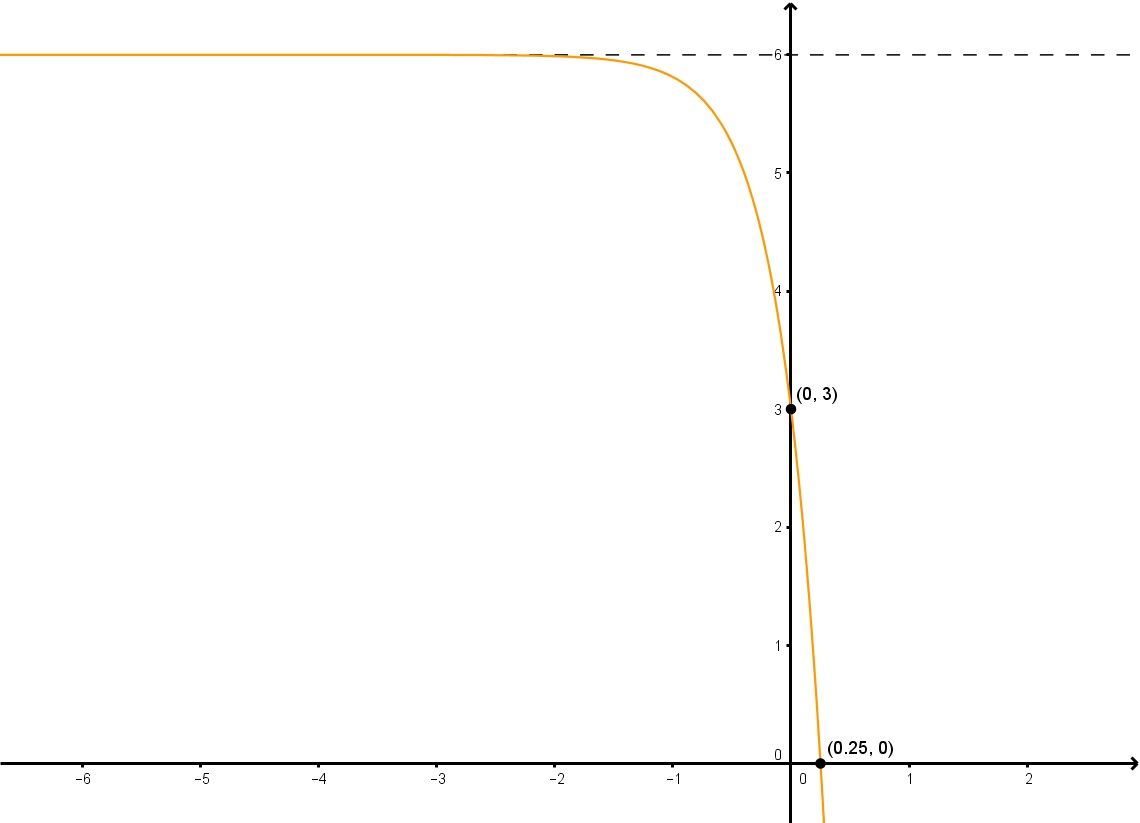
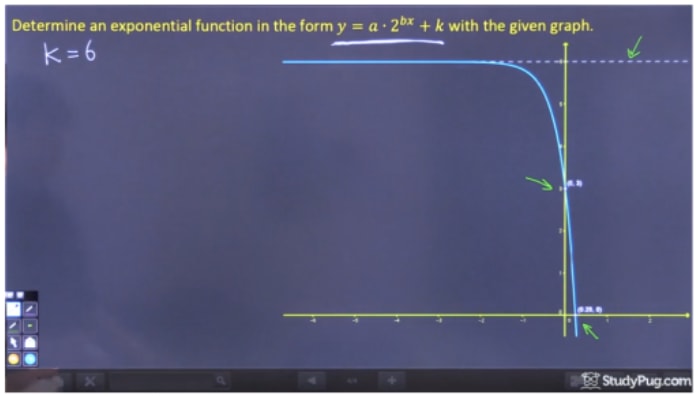
Schritt 1: Finde „k“ aus dem Graphen

Um „k“ zu finden, müssen wir nur die horizontale Asymptote finden, die eindeutig y=6 ist. Daher ist k=6.

Schritt 2: Löse für „a“

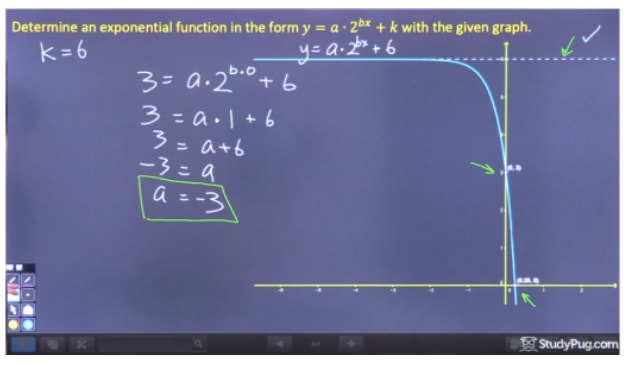
Schritt 3: Lösen Sie für „b“

Schritt 4: Schreiben Sie die endgültige Gleichung

Und das war’s für Exponentialfunktionen! Auch diese Funktionen sind etwas komplexer als Gleichungen für Geraden oder Parabeln, daher sollten Sie unbedingt viele Übungsaufgaben machen, um sich mit den neuen Variablen und Techniken vertraut zu machen. Mit mehr Übung werden Exponentialgleichungen und die Graphen von Exponentialfunktionen bald kein Problem mehr sein!