10.2 – Autocorrélation et méthodes des séries temporelles

Une façon courante pour que la condition d' »indépendance » dans un modèle de régression linéaire multiple échoue est lorsque les données de l’échantillon ont été recueillies au fil du temps et que le modèle de régression ne parvient pas à capturer efficacement toute tendance temporelle. Dans ce cas, les erreurs aléatoires du modèle sont souvent positivement corrélées dans le temps, de sorte que chaque erreur aléatoire est plus susceptible d’être similaire à l’erreur aléatoire précédente que si les erreurs aléatoires étaient indépendantes les unes des autres. Ce phénomène est connu sous le nom d’autocorrélation (ou corrélation sérielle) et peut parfois être détecté en traçant les résidus du modèle en fonction du temps. Nous l’explorerons plus en détail dans cette section et la suivante.

Une série chronologique est une séquence de mesures de la ou des mêmes variables effectuées au fil du temps. Habituellement, les mesures sont effectuées à des moments régulièrement espacés – par exemple, mensuellement ou annuellement. Considérons d’abord le problème dans lequel nous avons une variable y mesurée comme une série temporelle. Par exemple, nous pourrions avoir y une mesure de la température globale, avec des mesures observées chaque année. Pour souligner le fait que nous avons mesuré des valeurs dans le temps, nous utilisons l’indice  » t  » plutôt que l’indice  » i  » habituel, c’est-à-dire que \(y_t\) signifie \(y\) mesuré au cours de la période \(t\). On parle de modèle autorégressif lorsqu’une valeur d’une série temporelle est régressée sur les valeurs précédentes de cette même série temporelle. par exemple, \(y_{t}\) sur \(y_{t-1}\):

Dans ce modèle de régression, la variable de réponse de la période précédente est devenue le prédicteur et les erreurs ont nos hypothèses habituelles sur les erreurs dans un modèle de régression linéaire simple. L’ordre d’une autorégression est le nombre de valeurs immédiatement précédentes dans la série qui sont utilisées pour prédire la valeur au moment présent. Ainsi, le modèle précédent est une autorégression de premier ordre, écrite comme AR(1).

Si nous voulons prédire \(y\) cette année (\(y_{t}\)) à l’aide des mesures de la température mondiale des deux années précédentes (\(y_{t-1},y_{t-2}\)), alors le modèle autorégressif pour le faire serait :

Ce modèle est une autorégression de second ordre, écrite AR(2), puisque la valeur au temps $t$ est prédite à partir des valeurs aux temps \(t-1\) et \(t-2\). Plus généralement, une autorégression d’ordre \(k^{\textrm{th}}\), écrite AR(k), est une régression linéaire multiple dans laquelle la valeur de la série à tout moment t est une fonction (linéaire) des valeurs aux temps \(t-1,t-2,\ldots,t-k\).

Autocorrélation et autocorrélation partielle

Le coefficient de corrélation entre deux valeurs d’une série temporelle est appelé fonction d’autocorrélation (ACF) Par exemple, l’ACF pour une série temporelle \(y_t\) est donnée par :

Cette valeur de k est l’écart temporel considéré et est appelée le lag. Une autocorrélation lag 1 (c’est-à-dire k = 1 dans ce qui précède) est la corrélation entre des valeurs qui sont séparées par une période de temps. Plus généralement, une autocorrélation lag k est la corrélation entre des valeurs qui sont séparées par k périodes de temps.

L’ACF est un moyen de mesurer la relation linéaire entre une observation au temps t et les observations aux temps précédents. Si nous supposons un modèle AR(k), alors nous pouvons souhaiter mesurer uniquement l’association entre \(y_{t}\) et \(y_{t-k}\) et filtrer l’influence linéaire des variables aléatoires qui se trouvent entre les deux (c’est-à-dire \(y_{t-1},y_{t-2},\ldots,y_{t-(k-1 )}\), ce qui nécessite une transformation sur la série temporelle. Ensuite, en calculant la corrélation de la série temporelle transformée, nous obtenons la fonction d’autocorrélation partielle (PACF).

La PACF est surtout utile pour identifier l’ordre d’un modèle autorégressif. Plus précisément, les autocorrélations partielles de l’échantillon qui sont significativement différentes de 0 indiquent des termes retardés de \(y\) qui sont des prédicteurs utiles de \(y_{t}\). Il est important que le choix de l’ordre ait un sens. Par exemple, supposons que vous disposiez de mesures de pression artérielle pour chaque jour des deux dernières années. Vous pouvez trouver qu’un modèle AR(1) ou AR(2) est approprié pour modéliser la pression artérielle. Cependant, le PACF peut indiquer une grande valeur d’autocorrélation partielle à un retard de 17, mais un ordre aussi grand pour un modèle autorégressif n’a probablement pas beaucoup de sens.

Exemple 1 : Données Google

L’ensemble de données (google_stock.txt) est constitué de n = 105 valeurs qui sont le cours de clôture d’une action de Google du 2-7-2005 au 7-7-2005. Nous allons analyser le jeu de données pour identifier l’ordre d’un modèle autorégressif. Un tracé des prix des actions en fonction du temps est présenté dans la figure ci-dessous :

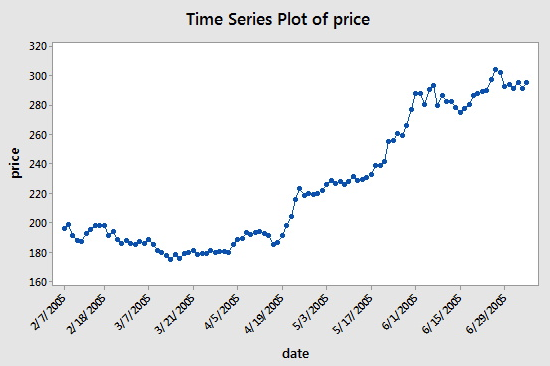
Les valeurs consécutives semblent se suivre assez étroitement, ce qui suggère qu’un modèle autorégressif pourrait être approprié. Nous examinons ensuite un graphique d’autocorrélations partielles pour les données :

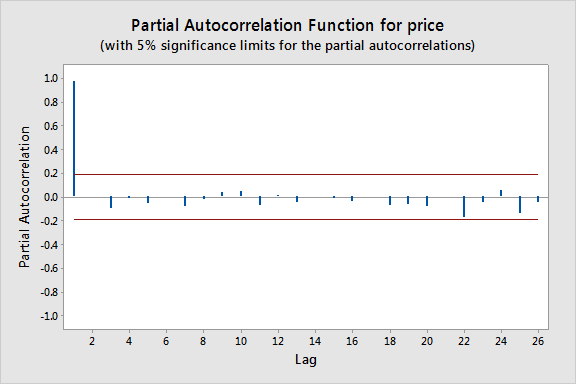
Ici, nous remarquons qu’il y a un pic significatif à un retard de 1 et des pics beaucoup plus faibles pour les retards suivants. Ainsi, un modèle AR(1) serait probablement réalisable pour cet ensemble de données.

Des limites approximatives peuvent également être construites (comme indiqué par les lignes rouges dans le tracé ci-dessus) pour ce tracé afin d’aider à déterminer les grandes valeurs. Les limites de signification approximatives \((1-\alpha)\times 100\%\) sont données par \(\pm z_{1-\alpha/2}/\sqrt{n}\). Les valeurs se situant en dehors de l’une ou l’autre de ces bornes indiquent un processus autorégressif.

Nous créons ensuite une variable de prix lag-1 et considérons un nuage de points du prix en fonction de cette variable lag-1 :

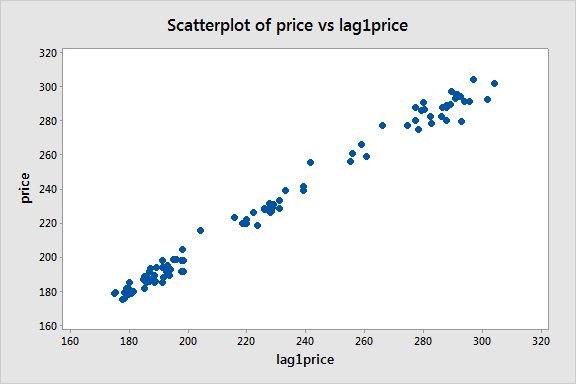
Il semble y avoir une forte tendance linéaire, affirmant que le modèle autorégressif de premier ordre

\

pourrait être utile.

Exemple 2 : Données sur les tremblements de terre

Laissons yt = le nombre annuel de tremblements de terre mondiaux de magnitude supérieure à 7 sur l’échelle de Richter pour n = 100 ans (données earthquakes.txt obtenues à partir de https://earthquake.usgs.gov). Le graphique ci-dessous donne un tracé de série temporelle pour cet ensemble de données.

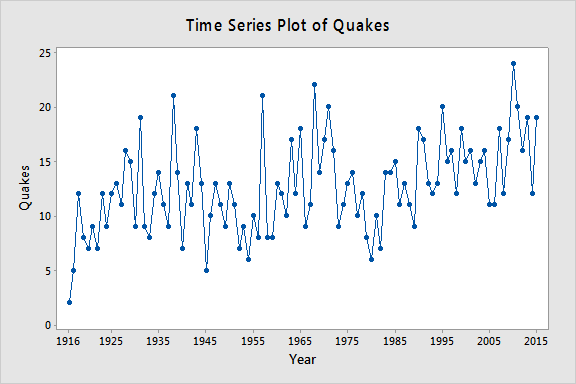
Le tracé ci-dessous donne un tracé de la PACF (fonction d’autocorrélation partielle), qui peut être interprété comme signifiant qu’une autorégression de troisième ordre peut être justifiée puisqu’il existe des autocorrélations partielles notables pour les lags 1 et 3.

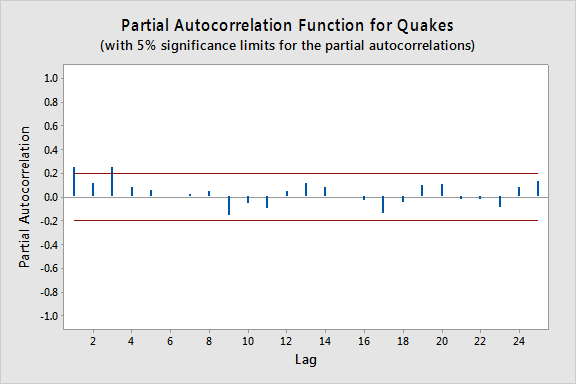
L’étape suivante consiste à effectuer une régression linéaire multiple avec le nombre de tremblements de terre comme variable de réponse et les tremblements de terre lag-1, lag-2 et lag-3 comme variables prédictives. Dans les résultats ci-dessous, nous voyons que la variable prédictive lag-3 est significative au niveau 0,05 (et la p-value de la variable prédictive lag-1 est également relativement faible).

.
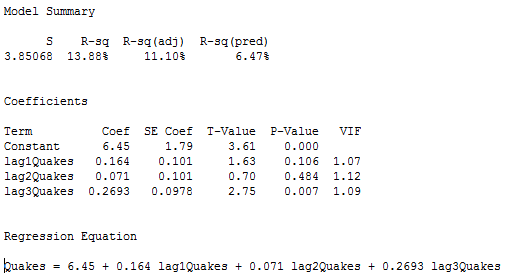