Algèbre du collège
Résultats d’apprentissage
- Convertir de la forme logarithmique à la forme exponentielle.
- Convertir de la forme exponentielle à la forme logarithmique.
Pour analyser l’ampleur des tremblements de terre ou comparer l’ampleur de deux tremblements de terre différents, nous devons être capables de convertir la forme logarithmique en forme exponentielle. Par exemple, supposons que la quantité d’énergie libérée par un tremblement de terre soit 500 fois supérieure à la quantité d’énergie libérée par un autre. Nous voulons calculer la différence de magnitude. L’équation qui représente ce problème est {10}^{x}=500 où x représente la différence de magnitude sur l’échelle de Richter. Comment résoudrions-nous x ?
Nous n’avons pas encore appris de méthode pour résoudre les équations exponentielles de manière algébrique. Aucun des outils algébriques abordés jusqu’à présent n’est suffisant pour résoudre {10}^{x}=500. Nous savons que {10}^{2}=100 et {10}^{3}=1000, il est donc clair que x doit être une valeur comprise entre 2 et 3 puisque y={10}^{x} est croissante. Nous pouvons examiner un graphique pour mieux estimer la solution.
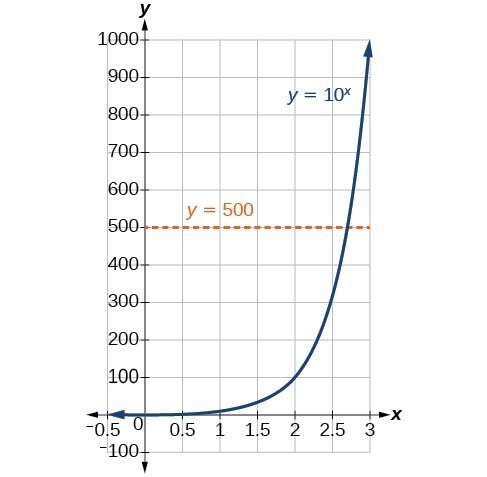
L’estimation à partir d’un graphique est cependant imprécise. Pour trouver une solution algébrique, nous devons introduire une nouvelle fonction. Observez que le graphique ci-dessus passe le test de la ligne horizontale. La fonction exponentielle y={b}^{x} est biunivoque, donc son inverse, x={b}^{y} est également une fonction. Comme c’est le cas pour toutes les fonctions inverses, il suffit d’intervertir x et y et de résoudre y pour trouver la fonction inverse. Pour représenter y en tant que fonction de x, nous utilisons une fonction logarithmique de la forme y={\mathrm{log}}_{b}\left(x\right). Le logarithme en base b d’un nombre est l’exposant par lequel nous devons élever b pour obtenir ce nombre.
Nous lisons une expression logarithmique de la manière suivante : » Le logarithme en base b de x est égal à y » ou, simplifié, » le logarithme en base b de x est égal à y « . Nous pouvons également dire « b élevé à la puissance de y est égal à x », car les logarithmes sont des exposants. Par exemple, le logarithme base 2 de 32 est 5, car 5 est l’exposant que nous devons appliquer à 2 pour obtenir 32. Puisque {2}^{5}=32, nous pouvons écrire {\mathrm{log}}_{2}32=5. Nous lisons cela comme « le logarithme base 2 de 32 est 5. »
Nous pouvons exprimer la relation entre la forme logarithmique et sa forme exponentielle correspondante comme suit :
{\mathrm{log}}_{b}\left(x\right)=y\Leftrightarrow {b}^{y}=x,\text{}b>0,b\ne 1
Notez que la base b est toujours positive.
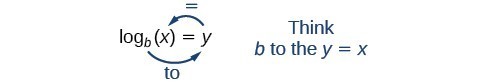
Parce qu’un logarithme est une fonction, il s’écrit le plus correctement sous la forme {\mathrm{log}}_{b}\left(x\right) en utilisant des parenthèses pour indiquer l’évaluation de la fonction tout comme nous le ferions avec f\left(x\right). Cependant, lorsque l’entrée est une variable ou un nombre unique, il est courant de ne pas utiliser de parenthèses et d’écrire l’expression sans parenthèses sous la forme {\mathrm{log}}_{b}x. Notez que de nombreuses calculatrices exigent des parenthèses autour du x.
Nous pouvons illustrer la notation des logarithmes comme suit :
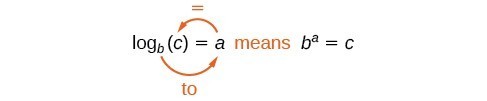
Notez que lorsque vous comparez la fonction logarithme et la fonction exponentielle, l’entrée et la sortie sont interverties. Cela signifie que y={\mathrm{log}}_{b}\left(x\right) et y={b}^{x} sont des fonctions inverses.
Une note générale : définition de la fonction logarithmique
Un logarithme de base b d’un nombre positif x répond à la définition suivante :
Pour x>0,b>0,b\ne 1,
y={\mathrm{log}}_{b}\left(x\right)\text{ est égal à }{b}^{y}=x, où
- on lit {\mathrm{log}}_{b}\left(x\right) comme, « le logarithme en base b de x » ou le « log base b de x. »
- Le logarithme y est l’exposant auquel il faut élever b pour obtenir x.
- Si aucune base b n’est indiquée, la base du logarithme est supposée être 10.
De plus, comme les fonctions logarithmique et exponentielle commutent les valeurs x et y, le domaine et l’étendue de la fonction exponentielle sont intervertis pour la fonction logarithmique. Par conséquent,
- le domaine de la fonction logarithme avec base b \text{ est} \left(0,\infty \right).
- l’étendue de la fonction logarithme avec base b \text{ est} \left(-\infty ,\infty \right).
Q & A
Peut-on prendre le logarithme d’un nombre négatif ?
Non. Comme la base d’une fonction exponentielle est toujours positive, aucune puissance de cette base ne peut jamais être négative. Nous ne pouvons jamais prendre le logarithme d’un nombre négatif. De même, on ne peut pas prendre le logarithme de zéro. Les calculatrices peuvent sortir le logarithme d’un nombre négatif lorsqu’elles sont en mode complexe, mais le logarithme d’un nombre négatif n’est pas un nombre réel.
Comment faire : étant donné une équation sous forme logarithmique {\mathrm{log}}_{b}\left(x\right)=y, la convertir sous forme exponentielle
- Examiner l’équation y={\mathrm{log}}_{b}x et identifier b, y et x.
- Réécrivez {\mathrm{log}}_{b}x=y comme {b}^{y}=x.
Exemple : Conversion de la forme logarithmique à la forme exponentielle
Écrire les équations logarithmiques suivantes sous forme exponentielle.
- {\mathrm{log}_{6}\left(\sqrt{6}\right)=\frac{1}{2}
- {\mathrm{log}_{3}\left(9\right)=2
Try It
Écrivez les équations logarithmiques suivantes sous forme exponentielle.
- {\mathrm{log}}_{10}\left(1,000,000\right)=6
- {\mathrm{log}_{5}\left(25\right)=2
Conversion de la forme exponentielle en forme logarithmique
Pour convertir la forme exponentielle en forme logarithmique, on suit les mêmes étapes en sens inverse. Nous identifions la base b, l’exposant x et la sortie y. Puis nous écrivons x={\mathrm{log}}_{b}\left(y\right).
Exemple : Conversion de la forme exponentielle à la forme logarithmique
Écrire les équations exponentielles suivantes sous forme logarithmique.
- {2}^{3}=8
- {5}^{2}=25
- {10}^{-4}=\frac{1}{10,000}
Try It
Écrivez les équations exponentielles suivantes sous forme logarithmique.
- {3}^{2}=9
- {5}^{3}=125
- {2}^{-1}=\frac{1}{2}
Contribuez !
Améliorer cette pageEn savoir plus