Applications de l’amplificateur opérationnel
Le premier exemple est l’amplificateur différentiel, à partir duquel de nombreuses autres applications peuvent être dérivées, notamment l’amplificateur inverseur, non inverseur et sommateur, le suiveur de tension, l’intégrateur, le différentiateur et le gyrateur.
Amplificateur différentiel (amplificateur de différence)Edit

Amplifie la différence de tension entre ses entrées.
Le nom « amplificateur différentiel » ne doit pas être confondu avec le « différentiateur », qui est également présenté sur cette page. L' »amplificateur d’instrumentation », qui est également présenté sur cette page, est une modification de l’amplificateur différentiel qui offre également une impédance d’entrée élevée.
Le circuit illustré calcule la différence de deux tensions, multipliée par un certain facteur de gain. La tension de sortie
V out = ( R f + R 1 ) R g ( R g + R 2 ) R 1 V 2 – R f R 1 V 1 = ( R 1 + R f R 1 ) ⋅ ( R g R g + R 2 ) V 2 – R f R 1 V 1 . {\displaystyle V_{\text{out}}={\frac {\left(R_{\text{f}}+R_{1}\right)R_{\text{g}}}{\left(R_{\text{g}}+R_{2}\right)R_{1}}}V_{2}-{\frac {R_{\text{f}}}{R_{1}}}V_{1}=\left({\frac {R_{1}+R_{\text{f}}}{R_{1}}}\right)\cdot \left({\frac {R_{\text{g}}}{R_{\text{g}}+R_{2}}}\right)V_{2}-{\frac {R_{\text{f}}}{R_{1}}}V_{1}.}

Or, exprimé en fonction de l’entrée en mode commun Vcom et de l’entrée différentielle Vdif :
V com = ( V 1 + V 2 ) / 2 ; V dif = V 2 – V 1 , {\displaystyle V_{\text{com}}=(V_{1}+V_{2})/2 ;V_{\text{dif}}=V_{2}-V_{1},}

La tension de sortie est
V out R 1 R f = V com R 1 / R f – R 2 / R g 1 + R 2 / R g + V dif 1 + ( R 2 / R g + R 1 / R f ) / 2 1 + R 2 / R g . {\displaystyle V_{\text{out}}{\frac {R_{1}}{R_{\text{f}}}}=V_{\text{com}}{\frac {R_{1}/R_{\text{f}}-R_{2}/R_{\text{g}}}{1+R_{2}/R_{\text{g}}}}+V_{\text{dif}}{\frac {1+(R_{2}/R_{\text{g}}+R_{1}/R_{\text{f}})/2}{1+R_{2}/R_{\text{g}}}}.}

Pour que ce circuit produise un signal proportionnel à la différence de tension des bornes d’entrée, le coefficient du terme Vcom (le gain en mode commun) doit être nul, ou
R 1 / R f = R 2 / R g . {\displaystyle R_{1}/R_{\text{f}}=R_{2}/R_{\text{g}.}

Avec cette contrainte en place, le rapport de réjection en mode commun de ce circuit est infiniment grand, et la sortie
V out = R f R 1 V dif = R f R 1 ( V 2 – V 1 ) , {\displaystyle V_{\text{out}}={\frac {R_{\text{f}}}{R_{1}}}V_{\text{dif}}={\frac {R_{\text{f}}}{R_{1}}}\left(V_{2}-V_{1}\right),}

où l’expression simple Rf / R1 représente le gain en boucle fermée de l’amplificateur différentiel.
Le cas particulier où le gain en boucle fermée est unitaire est un suiveur différentiel, avec
V out = V 2 – V 1 . {\displaystyle V_{\text{out}}=V_{2}-V_{1}.}

Amplificateur inverseurEdit
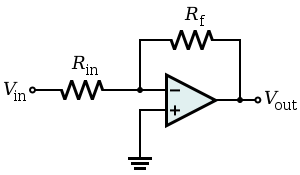
Un amplificateur inverseur est un cas particulier de l’amplificateur différentiel dans lequel l’entrée non-inverseuse V2 de ce circuit est mise à la masse, et l’entrée inverseuse V1 est identifiée à Vin ci-dessus. Le gain en boucle fermée est Rf / Rin, donc
V out = – R f R in V in {\displaystyle V_{\text{out}}=-{\frac {R_{\text{f}}{R_{\text{in}}}}V_{\text{in}}\ !}\,}

.
Le circuit simplifié ci-dessus est comme l’amplificateur différentiel dans la limite de R2 et Rg très petits. Dans ce cas, cependant, le circuit sera sensible à la dérive du courant de polarisation d’entrée à cause de l’inadéquation entre Rf et Rin.
Pour voir intuitivement l’équation de gain ci-dessus, calculer le courant dans Rin:
i in = V dans R in {\displaystyle i_{\text{in}}={\frac {V_{\text{in}}{R_{\text{in}}}}}

Alors rappelons que ce même courant doit passer par Rf, donc (car V- = V+ = 0) :
V out = – i in R f = – V in R f R in {\displaystyle V_{\text{out}}=-i_{\text{in}}R_{\text{f}}=-V_{\text{in}}{\frac {R_{\text{f}}{R_{\text{in}}}}}}

Une analogie mécanique est une bascule, avec le nœud V- (entre Rin et Rf) comme point d’appui, au potentiel de la terre. Vin est à une longueur Rin du point d’appui ; Vout est à une longueur Rf. Lorsque Vin descend « sous la terre », la sortie Vout augmente proportionnellement pour équilibrer la bascule, et vice versa.
Comme l’entrée négative de l’ampli-op agit comme une terre virtuelle, l’impédance d’entrée de ce circuit est égale à Rin.
Amplificateur non inverseurEdit
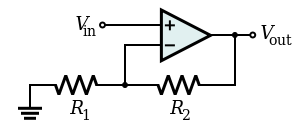
Un amplificateur non-inverseur est un cas particulier de l’amplificateur différentiel dans lequel l’entrée inverseuse V1 de ce circuit est mise à la terre, et l’entrée non-inverseuse V2 est identifiée à Vin ci-dessus, avec R1 ≫ R2.En se référant au circuit immédiatement supérieur,
V out = ( 1 + R 2 R 1 ) V in {\displaystyle V_{\text{out}}=\left(1+{\frac {R_{\text{2}}{R_{\text{1}}}}\right)V_{\text{in}}\ !}\,}

.
Pour voir intuitivement cette équation de gain, utilisez la technique de la masse virtuelle pour calculer le courant dans la résistance R1 :
i 1 = V dans R 1 , {\displaystyle i_{1}={\frac {V_{\text{in}}{R_{1}}}\,,}

alors rappelons que ce même courant doit passer par R2, donc :
V out = V in + i 1 R 2 = V in ( 1 + R 2 R 1 ) {\displaystyle V_{\text{out}}=V_{\text{in}}+i_{1}R_{2}=V_{\text{in}}\left(1+{\frac {R_{2}{R_{1}}right)}

Contrairement à l’amplificateur inverseur, un amplificateur non-inverseur ne peut pas avoir un gain inférieur à 1.
Une analogie mécanique est un levier de classe 2, avec une borne de R1 comme point d’appui, au potentiel de la terre. Vin est à une longueur R1 du point d’appui ; Vout est à une longueur R2 plus loin. Lorsque Vin monte » au-dessus du sol « , la sortie Vout augmente proportionnellement au levier.
L’impédance d’entrée de l’amplificateur non inverseur simplifié est élevée :
Z in = ( 1 + A OL B ) Z dif {\displaystyle Z_{\text{in}}=(1+A_{\text{OL}}B)Z_{\text{dif}}.

où Zdif est l’impédance d’entrée de l’ampli-op pour les signaux différentiels, et AOL est le gain en tension en boucle ouverte de l’ampli-op (qui varie avec la fréquence), et B est le facteur de rétroaction (la fraction du signal de sortie qui retourne à l’entrée). Dans le cas d’un ampli-op idéal, avec AOL infini et Zdif infini, l’impédance d’entrée est également infinie. Dans ce cas, cependant, le circuit sera sensible à la dérive du courant de polarisation d’entrée en raison du décalage entre les impédances pilotant les entrées V+ et V- de l’ampli-op.
La boucle de rétroaction diminue de la même manière l’impédance de sortie :
Z out = Z OL 1 + A OL B {\displaystyle Z_{\text{out}}={\frac {Z_{\text{OL}}{1+A_{\text{OL}B}}.

où Zout est l’impédance de sortie avec rétroaction, et ZOL est l’impédance de sortie en boucle ouverte.
Suiveur de tension (amplificateur tampon unitaire)

Utilisé comme amplificateur tampon pour éliminer les effets de charge (par ex, connecter un dispositif avec une impédance de source élevée à un dispositif avec une faible impédance d’entrée).
V out = V in {\displaystyle V_{\text{out}}=V_{\text{in}}\!}

Z in = ∞ {\displaystyle Z_{\text{in}}=\infty }

(de manière réaliste, l’impédance d’entrée différentielle de l’amplificateur opérationnel lui-même (1 MΩ à 1 TΩ), multipliée par le gain en boucle ouverte de l’amplificateur opérationnel)
En raison de la forte rétroaction (c’est-à-dire le gain unitaire) et de certaines caractéristiques non idéales des amplificateurs opérationnels réels, ce système de rétroaction est susceptible d’avoir de mauvaises marges de stabilité. Par conséquent, le système peut être instable lorsqu’il est connecté à des charges suffisamment capacitives. Dans ces cas, un réseau de compensation de retard (par exemple, en reliant la charge au suiveur de tension par une résistance) peut être utilisé pour rétablir la stabilité. La fiche technique du fabricant de l’amplificateur opérationnel peut fournir des indications pour la sélection des composants des réseaux de compensation externes. On peut également choisir un autre amplificateur opérationnel qui possède une compensation interne plus appropriée.
L’impédance d’entrée et de sortie est affectée par la boucle de rétroaction de la même manière que l’amplificateur non inverseur, avec B=1.
Amplificateur sommateurÉditer
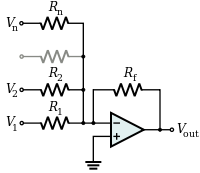
Un amplificateur sommateur additionne plusieurs tensions (pondérées) :
V out = – R f ( V 1 R 1 + V 2 R 2 + ⋯ + V n R n ) {\displaystyle V_{\text{out}}=-R_{\text{f}}\left({\frac {V_{1}}{R_{1}}+{\frac {V_{2}}{R_{2}}+\cdots +{\frac {V_{n}}{R_{n}}\right)}

- Quand R 1 = R 2 = ⋯ = R n {\displaystyle R_{1}=R_{2}=\cdots =R_{n}
, et R f {\displaystyle R_{\text{f}}
indépendant
V out = – R f R 1 ( V 1 + V 2 + ⋯ + V n ) {\displaystyle V_{\text{out}=-{\frac {R_{\text{f}}{R_{1}}(V_{1}+V_{2}+\cdots +V_{n})\ !)}

- Quand R 1 = R 2 = ⋯ = R n = R f {\displaystyle R_{1}=R_{2}=\cdots =R_{n}=R_{\text{f}}
V out = – ( V 1 + V 2 + ⋯ + V n ) {\displaystyle V_{\text{out}=-(V_{1}+V_{2}+\cdots +V_{n})}

- La sortie est inversée
- L’impédance d’entrée de la nième entrée est Z n = R n {\displaystyle Z_{n}=R_{n}}
( V – {\displaystyle V_{-}}
est une masse virtuelle)
Amplificateur d’instrumentationEdit
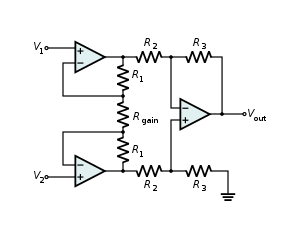
.




