Backpropagation étape par étape
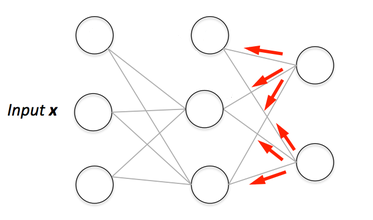 Si vous construisez votre propre réseau neuronal, vous aurez certainement besoin de comprendre comment le former.La rétro-propagation est une technique couramment utilisée pour former un réseau neuronal. Il existe de nombreuses ressources expliquant la technique, mais ce post expliquera la rétro-propagation avec un exemple concret dans des étapes colorées très détaillées.
Si vous construisez votre propre réseau neuronal, vous aurez certainement besoin de comprendre comment le former.La rétro-propagation est une technique couramment utilisée pour former un réseau neuronal. Il existe de nombreuses ressources expliquant la technique, mais ce post expliquera la rétro-propagation avec un exemple concret dans des étapes colorées très détaillées.
Vous pouvez voir la visualisation de la passe avant et de la rétro-propagation ici. Vous pouvez construire votre réseau neuronal en utilisant netflow.js
Overview
Dans ce post, nous allons construire un réseau neuronal avec trois couches :
- Couche d’entrée avec deux neurones d’entrée
- Une couche cachée avec deux neurones
- Couche de sortie avec un seul neurone
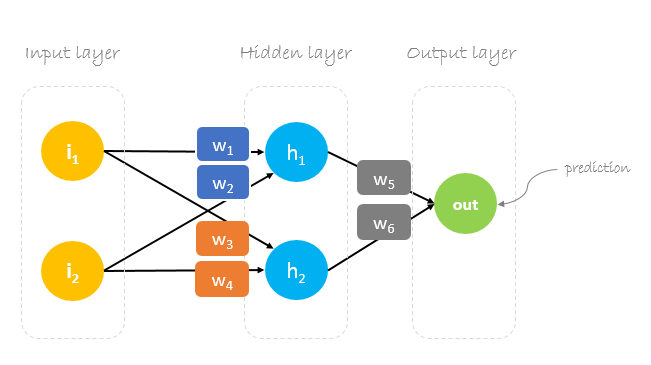
Poids, poids, poids
La formation d’un réseau neuronal consiste à trouver les poids qui minimisent l’erreur de prédiction. Nous commençons généralement notre formation avec un ensemble de poids générés aléatoirement.Ensuite, la rétropropagation est utilisée pour mettre à jour les poids dans une tentative de mapper correctement les entrées arbitraires aux sorties.
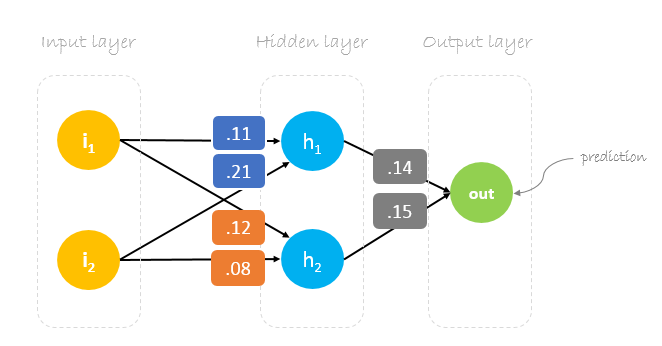
Nos poids initiaux seront les suivants :w1 = 0.11w2 = 0.21w3 = 0.12w4 = 0.08w5 = 0.14 et w6 = 0.15
Dataset
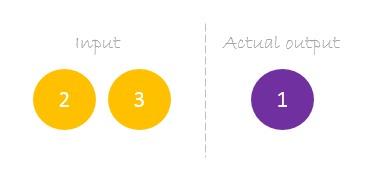
Notre dataset comporte un échantillon avec deux entrées et une sortie.
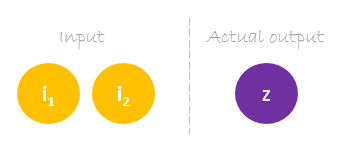
Notre échantillon unique est le suivant inputs= et output=.
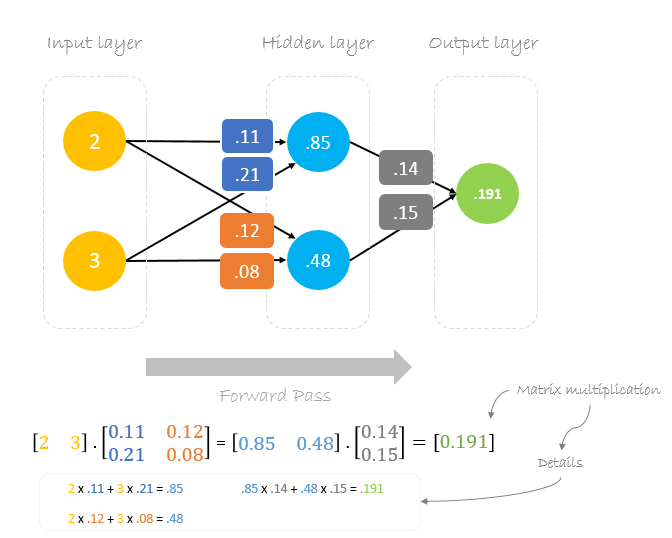
Forward Pass
Nous allons utiliser des poids et des entrées donnés pour prédire la sortie. Les entrées sont multipliées par les poids ; les résultats sont ensuite transmis à la couche suivante.
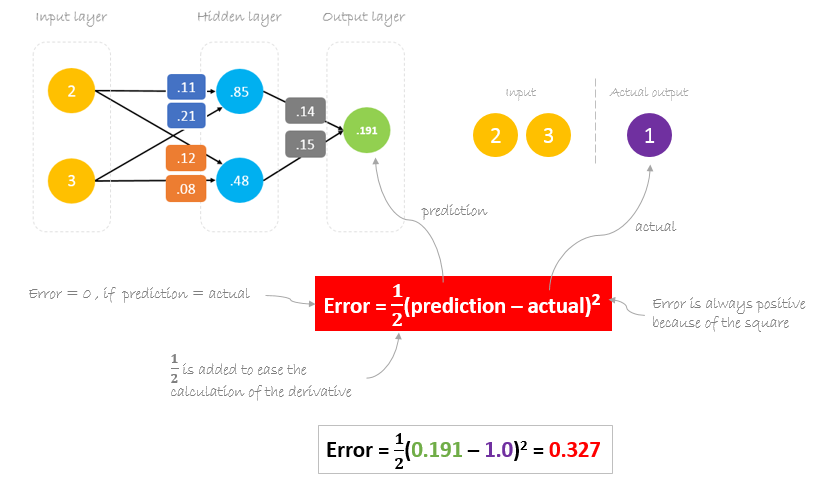
Calcul de l’erreur
Maintenant, il est temps de savoir comment notre réseau s’est comporté en calculant la différence entre la sortie réelle et celle prédite. Il est clair que la sortie de notre réseau, ou prédiction, n’est même pas proche de la sortie réelle. Nous pouvons calculer la différence ou l’erreur comme suit.
Réduire l’erreur
Notre objectif principal de la formation est de réduire l’erreur ou la différence entre la prédiction et la sortie réelle. Puisque la sortie réelle est constante, « ne change pas », la seule façon de réduire l’erreur est de changer la valeur de prédiction. La question est maintenant de savoir comment changer la valeur de prédiction ?
En décomposant la prédiction en ses éléments de base, nous pouvons trouver que les poids sont les éléments variables affectant la valeur de prédiction. En d’autres termes, pour changer la valeur de prédiction, nous devons changer les valeurs des poids.
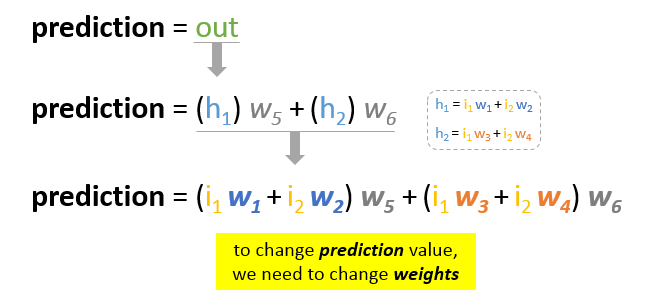
La question qui se pose maintenant est de savoir comment changer\upour mettre à jour la valeur des poids afin de réduire l’erreur ?
La réponse est la Backpropagation !
Backpropagation
La Backpropagation, abréviation de « backward propagation of errors », est un mécanisme utilisé pour mettre à jour les poids en utilisant la descente de gradient. Il calcule le gradient de la fonction d’erreur par rapport aux poids du réseau neuronal. Le calcul se fait à rebours dans le réseau.
La descente de gradient est un algorithme d’optimisation itératif permettant de trouver le minimum d’une fonction ; dans notre cas, nous voulons minimiser la fonction d’erreur. Pour trouver un minimum local d’une fonction en utilisant la descente de gradient, on prend des étapes proportionnelles au négatif du gradient de la fonction au point actuel.

Par exemple, pour mettre à jour w6, nous prenons la w6 actuelle et soustrayons la dérivée partielle de la fonction d’erreur par rapport à w6. En option, nous multiplions la dérivée de la fonction d’erreur par un nombre choisi pour nous assurer que le nouveau poids mis à jour minimise la fonction d’erreur ; ce nombre est appelé taux d’apprentissage.
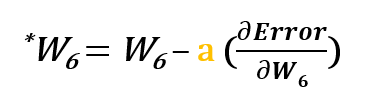
La dérivée de la fonction d’erreur est évaluée en appliquant la règle de la chaîne de la manière suivante
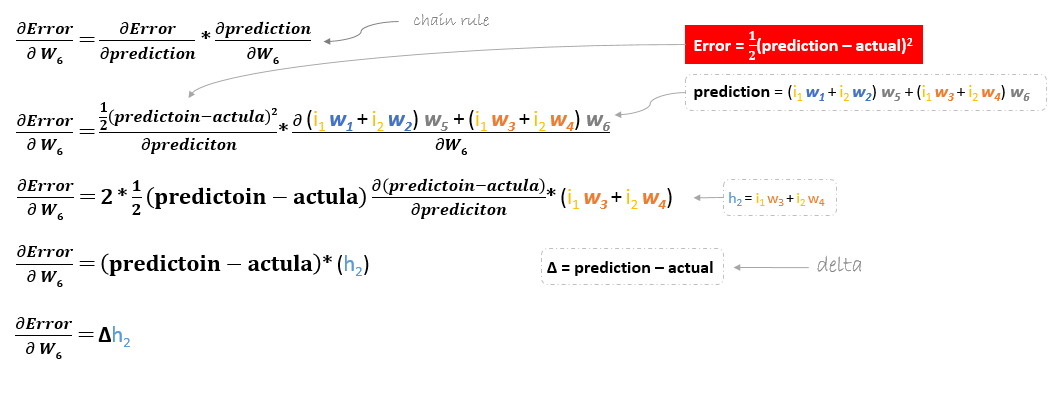
Donc pour mettre à jour w6 on peut appliquer la formule suivante
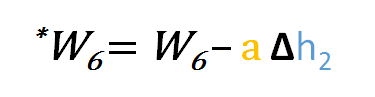
De même, nous pouvons dériver la formule de mise à jour pour w5 et tout autre poids existant entre la sortie et la couche cachée.
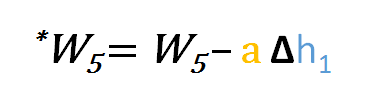
Cependant, lorsqu’on recule pour mettre à jour w1w2w3 et w4 existant entre l’entrée et la couche cachée, la dérivée partielle de la fonction d’erreur par rapport à w1, par exemple, sera la suivante.
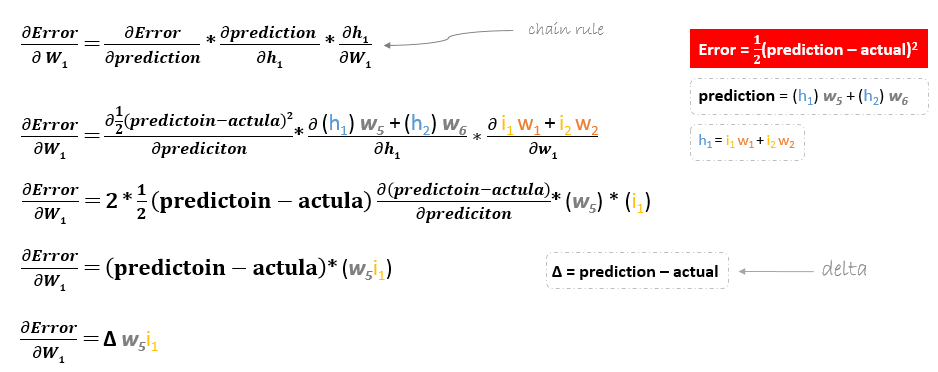
Nous pouvons trouver la formule de mise à jour des poids restants w2w3 et w4 de la même manière.
En résumé, les formules de mise à jour de tous les poids seront les suivantes :

Nous pouvons réécrire les formules de mise à jour en matrices de la manière suivante
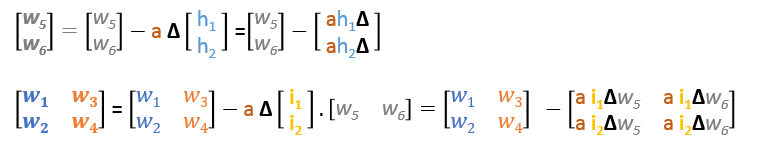
Passe en arrière
En utilisant les formules dérivées, nous pouvons trouver les nouveaux poids.
Taux d’apprentissage : est un hyperparamètre ce qui signifie que nous devons deviner manuellement sa valeur.

Maintenant, en utilisant les nouveaux poids, nous allons répéter le forward passé
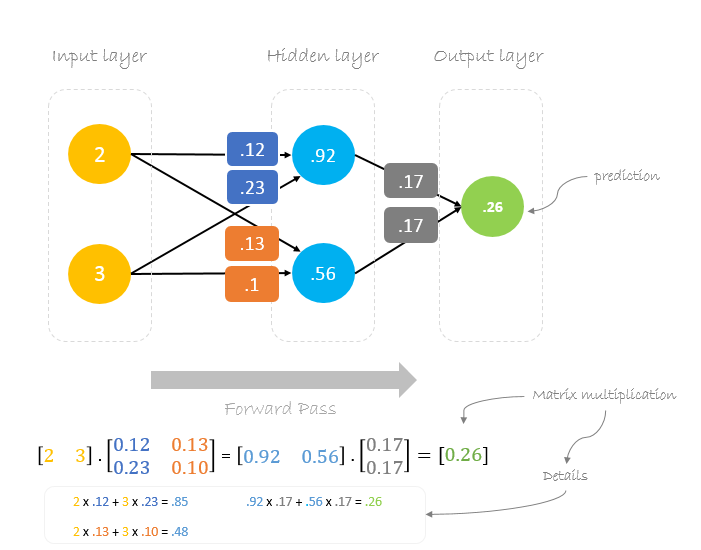
Nous pouvons remarquer que la prédiction 0.26 est un peu plus proche de la sortie réelle que celle précédemment prédite 0.191. Nous pouvons répéter le même processus de passage en arrière et en avant jusqu’à ce que l’erreur soit proche ou égale à zéro.
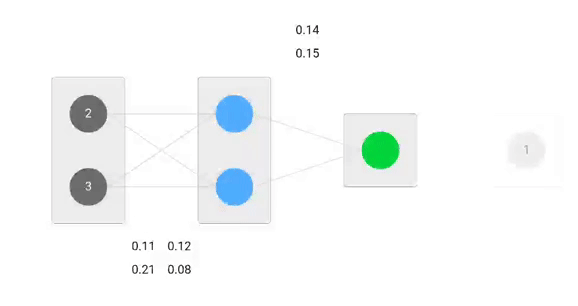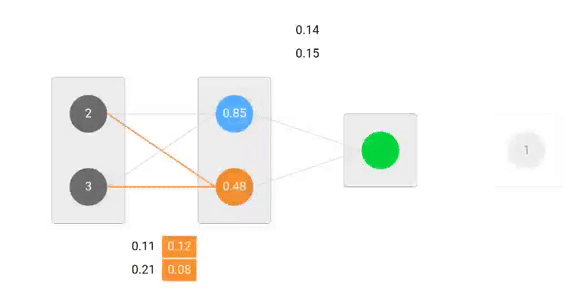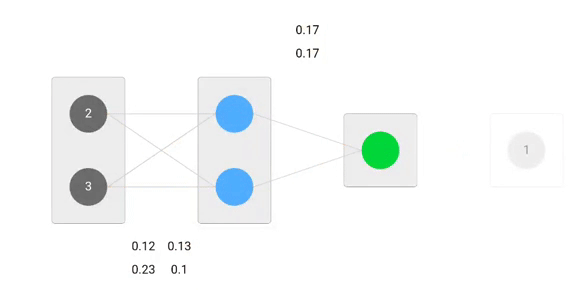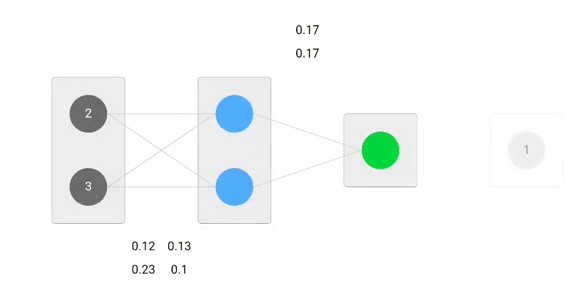
Visualisation de la rétropropagation
Vous pouvez voir la visualisation du passage en avant et de la rétropropagation ici.
Vous pouvez construire votre réseau neuronal à l’aide de netflow.js
.