Calculatrice de tension
Comment calculer la tension des cordes qui suspendent un objet
On peut voir dans l’illustration ci-dessous que la force, F, nécessaire pour soulever l’objet est égale au poids, W, de l’objet. Cette idée est le concept fondamental qui sous-tend notre formule de la force de tension. Vous trouverez également ci-dessous le diagramme de corps libre de l’objet qui montre les forces de tension, T, agissant sur la corde. Comme vous pouvez le voir, les forces de tension viennent par paires et dans des directions opposées :
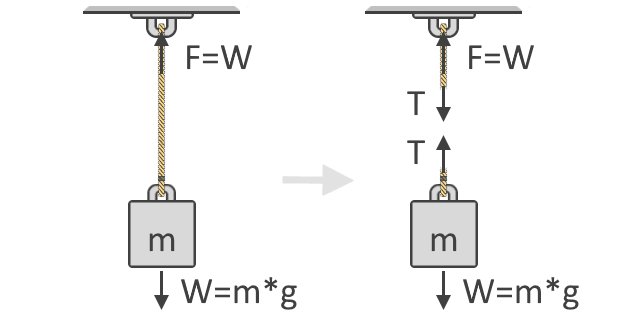
Suivant la deuxième loi du mouvement de Newton, nous pouvons alors exprimer la somme des forces à l’aide du diagramme de corps libre de l’objet, comme le montre la partie droite de l’illustration ci-dessus. Nous utilisons les diagrammes de corps libre pour montrer les différentes directions et amplitudes des forces qui agissent sur un corps. À l’équilibre, ces forces doivent toutes être égales à zéro. En considérant toutes les forces vers le haut comme positives et vers le bas comme négatives, notre équation est :
ΣF = 0 = T + (-W)T = W
où le poids, W, devient négatif puisqu’il est dirigé vers le bas. En transposant W à l’autre côté de l’équation, nous pouvons maintenant voir que la force de tension dans la corde est égale au poids de l’objet qu’elle porte, comme cela est également montré ci-dessus.
Si nous utilisons plus de cordes pour soulever l’objet, la force de tension totale se divise entre les cordes. La force de tension dans chaque corde dépend de leurs angles par rapport à la direction de la force à laquelle elle s’oppose. Pour mieux comprendre cela, considérons un autre diagramme de corps libre d’un objet suspendu par deux cordes, comme indiqué ci-dessous :
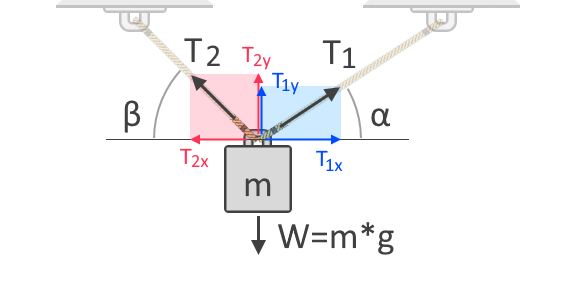
Dans le diagramme de corps libre présenté ci-dessus, nous pouvons voir les composantes horizontales et verticales des forces de tension, T₁, et T₂. Les forces sont des vecteurs, ce qui signifie qu’elles ont toujours une magnitude et une direction. Comme tous les vecteurs, les forces peuvent être exprimées par ces composantes qui donnent l’influence de la force le long des axes horizontal et vertical. T₁ₓ et T₂ₓ sont les composantes verticales de T₁ et T₂, respectivement. D’autre part, T₁ᵧ et T₂ᵧ sont les composantes verticales des mêmes forces, respectivement. Puisque la gravité agit sur l’objet selon l’axe vertical, nous devons considérer les composantes verticales des forces de tension pour notre sommation des forces comme suit :
ΣF = 0 = T₁ᵧ + T₂ᵧ + (-W)W = T₁ᵧ + T₂ᵧ
Parce que nous connaissons également les angles des forces de tension, nous pouvons exprimer T₁ᵧ et T₂ᵧ en termes de T₁ et T₂, respectivement, à l’aide de fonctions trigonométriques :
T₁ᵧ = T₁ * sin(α)T₂ᵧ = T₂ * sin(β)W = T₁ * sin(α) + T₂ * sin(β)
On peut aussi dire que pour que le système soit en équilibre, l’objet ne doit pas se déplacer horizontalement ou selon l’axe des x. Par conséquent, les composantes horizontales de T₁ et T₂ doivent alors être égales à zéro. Aussi, à l’aide de la trigonométrie, nous pouvons exprimer T₁ₓ et T₂ₓ en termes de T₁ et T₂, respectivement :
T₁ₓ = T₂ₓT₁ * cos(α) = T₂ * cos(β)
Si nous divisons les deux côtés par cos(α), nous obtenons une équation dans laquelle T₁ est exprimé en termes de T₂ et des angles :
T₁ = T₂ * cos(β) / cos(α)
Nous pouvons ensuite utiliser cette équation pour résoudre T₂ en substituant T₂ * cos(β) / cos(α) comme T₁ dans notre équation de sommation des forces, comme indiqué ci-dessous :
W = T₁ * sin(α) + T₂ * sin(β)W = T₂ * * sin(α) + T₂ * sin(β)W = T₂ * T₂ = W /
Enfin, si nous multiplions toute cette équation par cos(β) / cos(α) comme nous l’avons dérivé dans la valeur de T₁ en termes de T₂, puis en simplifiant tout, nous obtenons cette équation :
T₁ = W / * T₁ = W / * T₁ = W /
Maintenant, tout ce que vous devez savoir, ce sont les angles des cordes de tension par rapport à l’horizontale. Si un angle par rapport à la verticale est donné, il suffit de soustraire cet angle de 90°. En procédant ainsi, vous obtiendrez l’angle par rapport à l’horizontale. Toutefois, si vous obtenez d’autres valeurs d’angle, supérieures à 90° ou même à 180°, vous pouvez consulter notre calculatrice d’angle de référence pour vous aider à déterminer l’angle dont vous avez besoin. Après avoir déterminé les valeurs des variables dans nos formules de force de tension, nous pouvons maintenant résoudre les forces de tension.