Déterminer une fonction exponentielle étant donné son graphique – Fonctions exponentielles
Qu’est-ce que les fonctions exponentielles?
Avant de traiter les fonctions exponentielles et de tracer des graphiques de fonctions exponentielles, jetons d’abord un coup d’œil à la formule générale et à la théorie derrière les fonctions exponentielles.
Vous trouverez ci-dessous l’une des formes les plus générales d’un graphique exponentiel :

L’équation de la fonction exponentielle à ce graphique est y=2xy=2^xy=2x, et c’est le graphique exponentiel le plus simple que l’on puisse faire. Si vous vous demandez à quoi ressemblerait y=1xy=1^xy=1x, voici son graphique exponentiel :
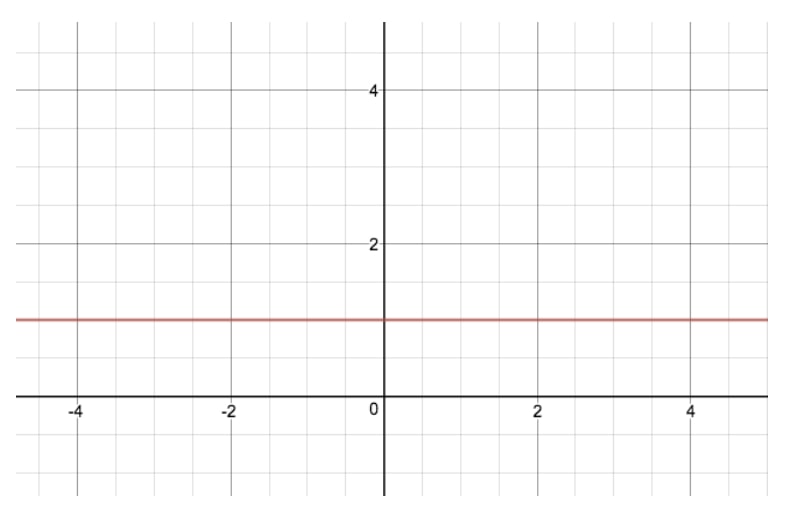
Maintenant, quant à savoir pourquoi les graphiques de y=2xy=2^xy=2x et y=1xy=1^xy=1x sont si différents, la meilleure façon de comprendre la théorie derrière les fonctions exponentielles est de jeter un coup d’œil à quelques tableaux.

Au-dessus, vous pouvez voir trois tableaux pour trois » valeurs de base » différentes – 1, 2 et 3 – qui sont toutes à la puissance de x. Comme vous pouvez le voir, pour les fonctions exponentielles avec une » valeur de base » de 1, la valeur de y reste constante à 1, car 1 à la puissance de n’importe quoi est juste 1. C’est pourquoi le graphique ci-dessus de y=1xy=1^xy=1x est juste une ligne droite. Dans le cas de y=2xy=2^xy=2x et de y=3xy=3^xy=3x (non illustré), par contre, nous voyons une courbe de plus en plus raide pour notre graphique. C’est parce que lorsque x augmente, la valeur de y augmente à chaque fois d’une valeur de plus en plus grande, ou ce que nous appelons « exponentiellement ».
Maintenant que nous avons une idée de ce à quoi ressemblent les équations exponentielles dans un graphique, donnons la formule générale des fonctions exponentielles :
y=abd(x-c)+ky=ab^{d(x-c)}+ky=abd(x-c)+k
La formule ci-dessus est un peu plus compliquée que les fonctions précédentes avec lesquelles vous avez probablement travaillé, alors définissons toutes les variables.
y – la valeur sur l’axe des y
a – le facteur d’étirement ou de compression verticale
b – la valeur de base
x – la valeur sur l’axe des x
c – le facteur de translation horizontale
d – le facteur d’étirement ou de compression horizontale
k – le facteur de translation verticale
Dans cette leçon, nous n’aborderons que les fonctions exponentielles très basiques, vous n’avez donc pas besoin de vous soucier de certaines des variables ci-dessus. Mais, pour que vous ayez accès à toutes les informations dont vous avez besoin sur les fonctions exponentielles et sur la façon de tracer un graphique des fonctions exponentielles, exposons ce que la modification de chacune de ces variables fait au graphique d’une équation exponentielle.
1) Variable « a »
Considérons le graphique de y=2xy=2^xy=2x à une autre équation exponentielle où nous modifions « a », ce qui nous donne y=(-4)2xy=(-4)2^xy=(-4)2x

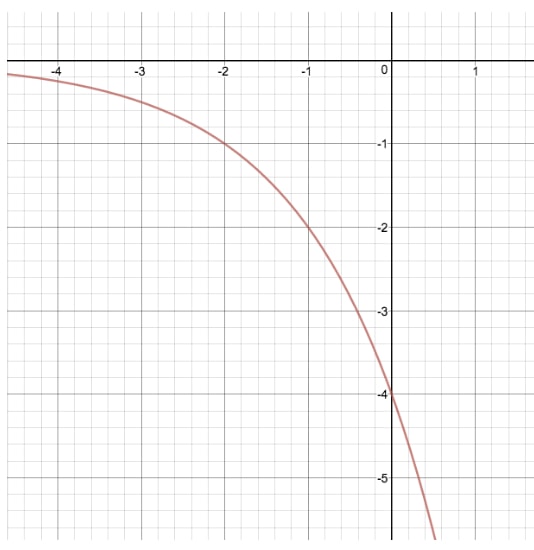
En effectuant cette transformation, nous avons à la fois « étiré » et « reflété » le graphique original de y=2xy=2^xy=2x par ses valeurs y. Pour trouver « a » en regardant le graphique, la chose la plus importante à noter est que lorsque x=0 et que nous n’avons pas de valeur pour « k », l’ordonnée à l’origine de notre graphique sera toujours égale à « a ».
2)Variable « b »
Aussi connue sous le nom de « valeur de base », c’est simplement le nombre auquel est attaché l’exposant. Le trouver implique l’algèbre, qui sera abordée plus loin dans cet article.
Variable « c »
Considérons le graphique de y=2xy=2^xy=2x à une autre équation exponentielle où nous modifions « c », ce qui nous donne y=2(x-2)y=2^{(x-2)}y=2(x-2)

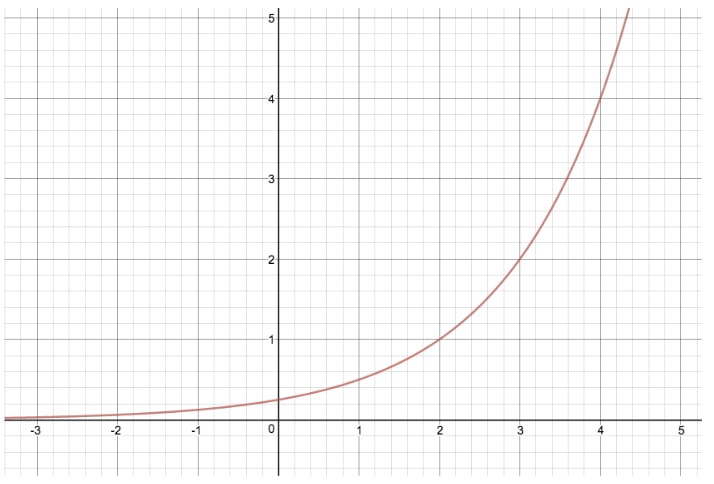
En effectuant cette transformation, nous avons déplacé le graphique entier de deux unités vers la droite. Si « c » était égal à -2, nous aurions déplacé l’ensemble du graphique vers la gauche de deux unités.
Variable « d »
Considérons le graphique de y=2xy=2^xy=2x à une autre équation exponentielle où nous modifions « d », ce qui nous donne y=24xy=2^{4x}y=24x

.
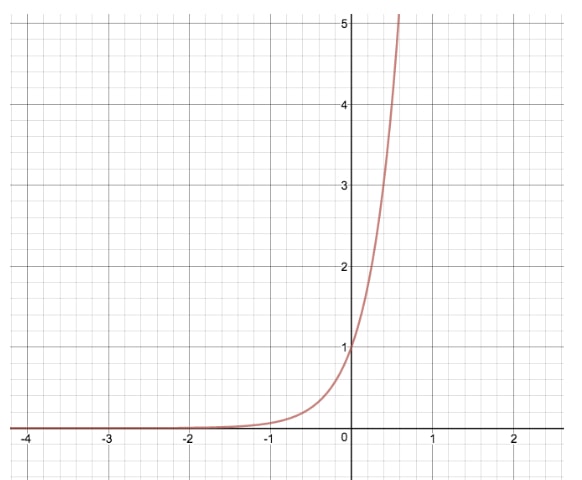
En effectuant cette transformation, nous avons étiré le graphique original de y=2xy=2^xy=2x par ses valeurs x, de la même manière que la variable « a » modifie la fonction par ses valeurs y. Si « d » était négatif dans cet exemple, la fonction exponentielle subirait une réflexion horizontale, par opposition à la réflexion verticale observée avec « a ».
Variable « k »
Considérons le graphique de y=2xy=2^xy=2x à une autre équation exponentielle où nous modifions « k », ce qui nous donne y=2x+2y=2^x+2y=2x+2

.
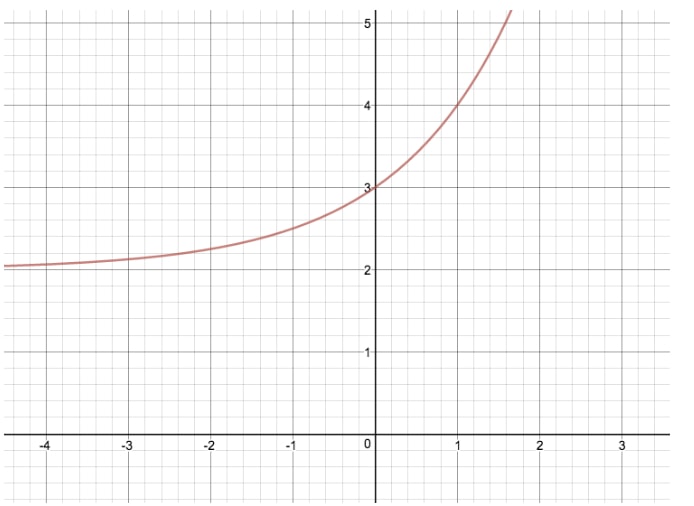
En effectuant cette transformation, nous avons augmenté de deux unités le graphique original de y=2xy=2^xy=2x. Si « k » était négatif dans cet exemple, la fonction exponentielle aurait été traduite vers le bas de deux unités. « k » est une variable particulièrement importante, car elle est également égale à ce que nous appelons l’asymptote horizontale ! Une asymptote est une valeur pour x ou y qu’une fonction approche, mais qu’elle n’égale jamais réellement.
Prenons par exemple la fonction y=2xy=2^xy=2x : pour cette fonction exponentielle, k=0, et donc l' » asymptote horizontale » est égale à 0. C’est logique, car quelle que soit la valeur que nous mettons pour x, nous n’obtiendrons jamais que y soit égal à 0. Pour notre autre fonction y=2x+2y=2^x+2y=2x+2, k=2, et donc l’asymptote horizontale est égale à 2. Il n’y a aucune valeur de x que nous puissions utiliser pour que y=2.
Et voilà pour toutes les variables ! Encore une fois, plusieurs d’entre elles sont plus compliquées que d’autres, il faudra donc du temps pour s’habituer à travailler avec toutes ces variables et devenir à l’aise pour les trouver. Pour mieux comprendre les fonctions exponentielles et vous familiariser avec l’équation générale ci-dessus, visitez le site Web de cette excellente calculatrice graphique. Prenez le temps de jouer avec les variables, et de mieux sentir comment le changement de chacune des variables affecte la nature de la fonction.
Maintenant, passons aux choses sérieuses. Étant donné le graphique d’une fonction exponentielle, comment pouvons-nous trouver l’équation exponentielle ?
Comment trouver les fonctions exponentielles
Trouver l’équation des fonctions exponentielles est souvent un processus en plusieurs étapes, et chaque problème est différent en fonction des informations et du type de graphique qui nous est donné. Étant donné le graphique des fonctions exponentielles, nous devons être capables de prendre certaines informations à partir du graphique lui-même, puis de résoudre les choses que nous ne pouvons pas prendre directement à partir du graphique. Vous trouverez ci-dessous une liste de toutes les variables que nous pouvons avoir à chercher, et comment les trouver habituellement :
a – résolvez-la en utilisant l’algèbre, ou elle sera donnée
b – résolvez-la en utilisant l’algèbre, ou elle sera donnée
c – laissez x = 0 et imaginez que « c » n’est pas là, la valeur de y sera égale à l’ordonnée à l’origine ; comptez maintenant combien d’unités la valeur de y pour l’ordonnée à l’origine se trouve à partir de l’axe des y, et cela sera égal à » c «
d – résolvez-le en utilisant l’algèbre
k – égal à la valeur de l’asymptote horizontale
Bien sûr, ce ne sont que les étapes générales que vous devez suivre pour trouver l’équation de la fonction exponentielle. La meilleure façon d’apprendre à le faire est d’essayer quelques problèmes pratiques !
Exemples de fonctions exponentielles :
Maintenant, essayons quelques exemples afin de mettre en pratique toute la théorie que nous avons couverte. Avec de la pratique, vous serez en mesure de trouver des fonctions exponentielles avec facilité!
Exemple 1:
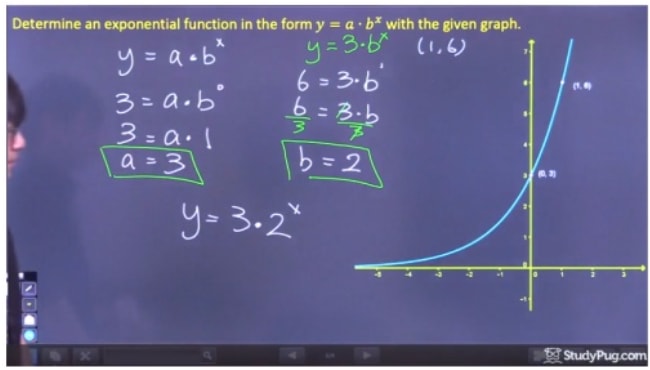
Déterminer la fonction exponentielle sous la forme y=abxy=ab^xy=abx du graphique donné.
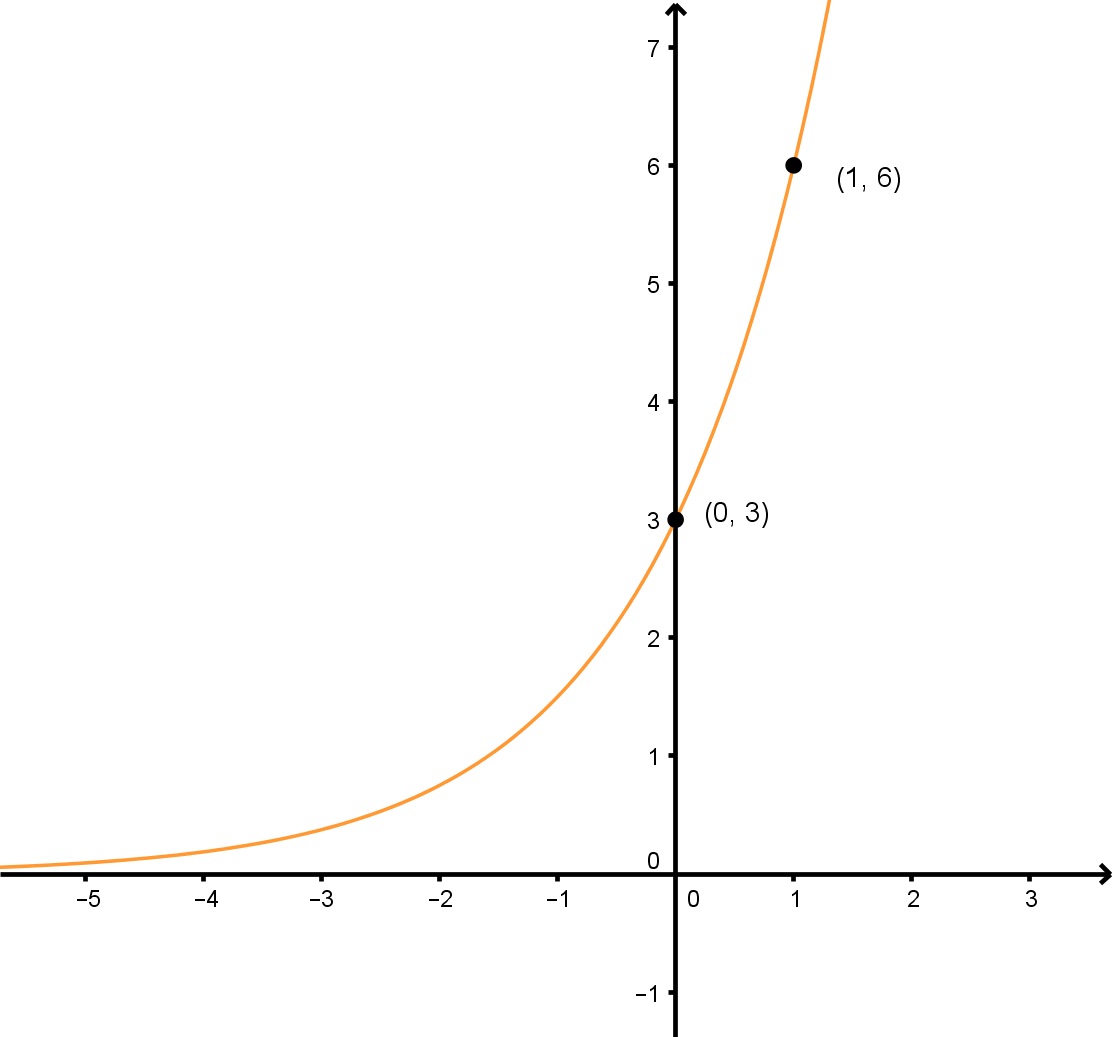
Pour résoudre ce problème, nous allons devoir trouver les variables « a » et « b ». De plus, nous allons devoir résoudre ces deux variables de façon algébrique, car nous ne pouvons pas les déterminer à partir du graphique de la fonction exponentielle lui-même.
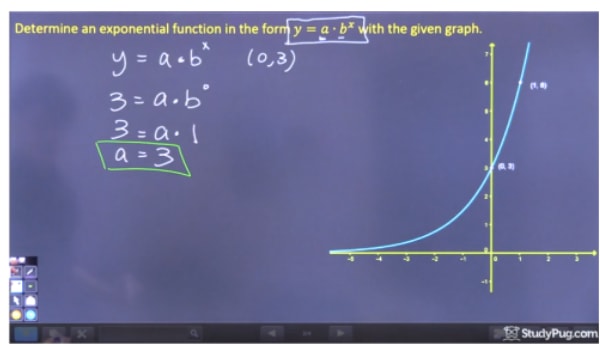
Étape 1 : Résoudre pour » a «
Pour résoudre » a « , nous devons choisir un point sur le graphique où nous pouvons éliminer bx, car nous ne connaissons pas encore » b « , et nous devons donc choisir l’ordonnée à l’origine (0,3). Puisque b0 est égal à 1, nous pouvons trouver que a=3. En guise de raccourci, puisque nous n’avons pas’ de valeur pour k, a est juste égal à l’ordonnée à l’origine de cette équation.
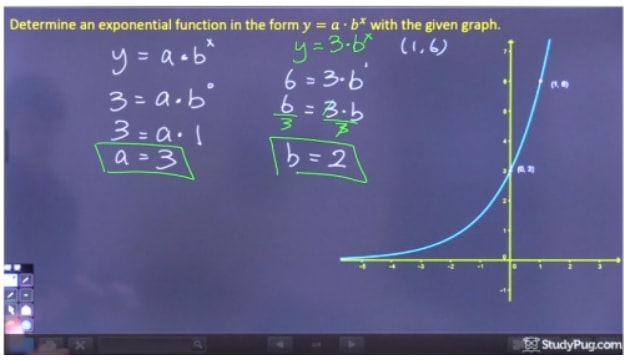
Étape 2 : Résoudre pour « b »
Étape 3 : Écrire l’équation finale
Exemple 2 :
Déterminer la fonction exponentielle de la forme y=a2dx+ky=a2^{dx}+ky=a2dx+k du graphique donné.
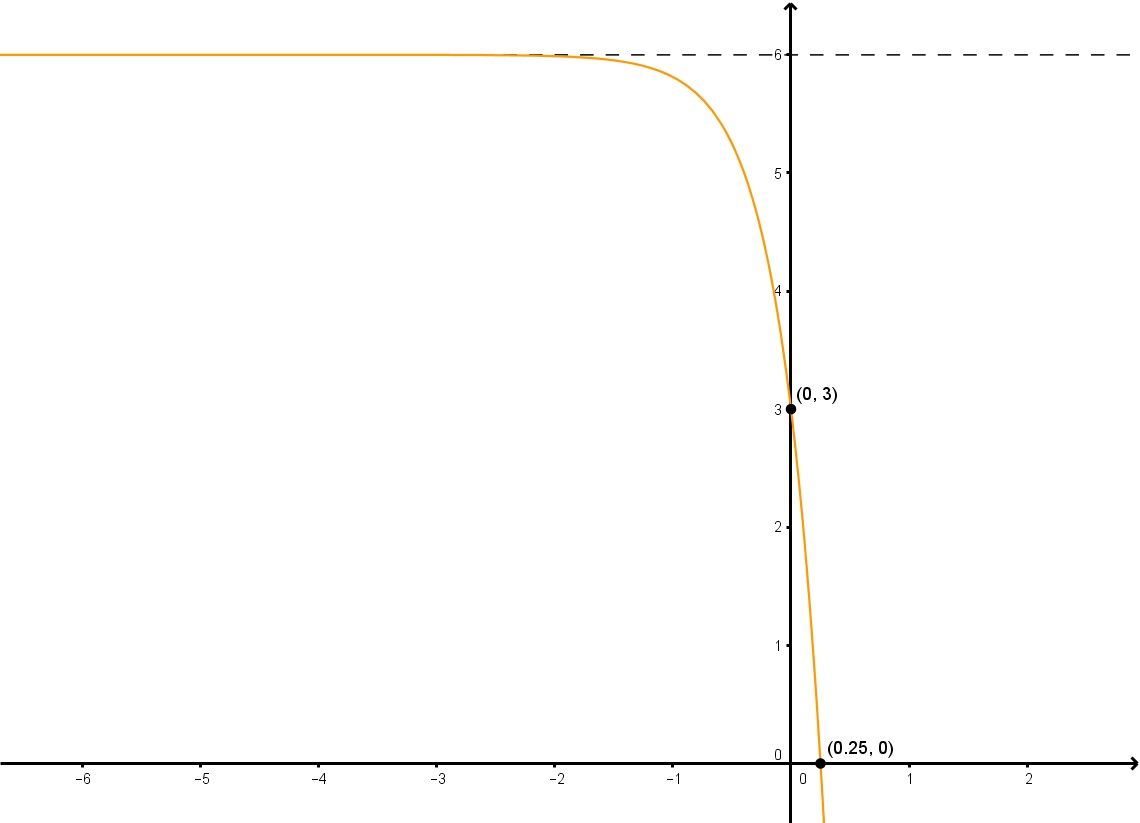
Étape 1 : Trouver » k » à partir du graphique
Pour trouver » k « , il suffit de trouver l’asymptote horizontale, qui est clairement y=6. Par conséquent, k=6.
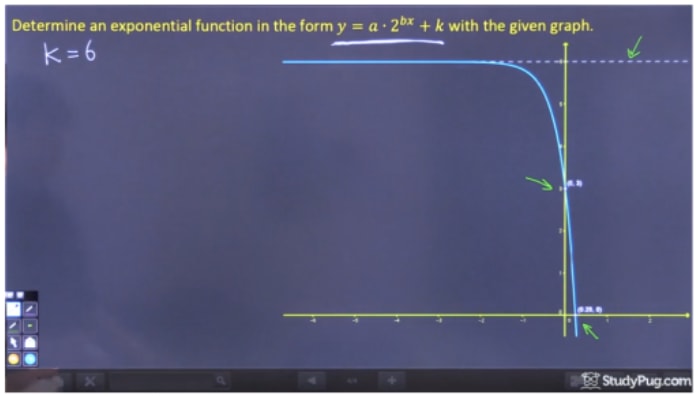
Étape 2 : Résoudre pour « a »
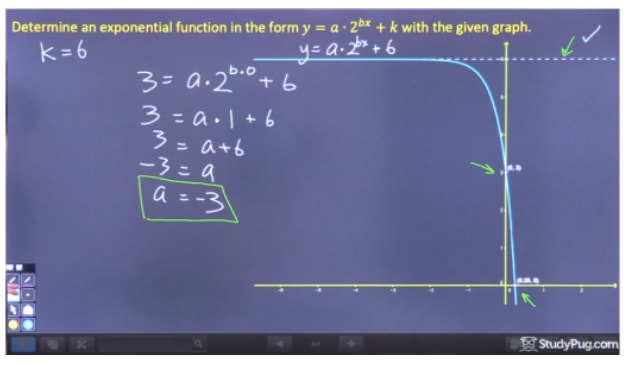
Étape 3 : Résoudre pour « b »

Étape 4 : Écrire l’équation finale

Et voilà pour les fonctions exponentielles ! Encore une fois, ces fonctions sont un peu plus complexes que les équations de droites ou de paraboles, alors assurez-vous de faire beaucoup de problèmes pratiques pour vous familiariser avec les nouvelles variables et techniques. Avec plus de pratique, bientôt, les équations exponentielles et les graphiques des fonctions exponentielles ne vous poseront plus aucun problème !
.