Factorielle

Qu’est-ce que la factorielle ?

La factorielle (dénotée ou représentée par n !) pour un nombre positif ou entier (qui est noté par n) est le produit de tous les nombres positifs précédant ou équivalant à n (l’entier positif). La fonction factorielle se retrouve dans divers domaines des mathématiques, notamment l’algèbre, l’analyse mathématique et la combinatoire.

Dès les années 1200, les factorielles étaient utilisées pour compter les permutations. La notation d’une factorielle (n !) a été introduite au début des années 1800 par Christian Kramp, un mathématicien français.

La formule de la factorielle peut être vue ci-dessous:

Définition de la factorielle

La fonction d’une factorielle est définie par le produit de tous les nombres entiers positifs antérieurs et/ou égaux à n, soit :

n ! = 1 ∙ 2 ∙ 3 ∙∙∙ (n-2) ∙ (n -1) ∙ n,

quand on considère des valeurs ou des entiers supérieurs ou égaux à 1. Elle peut alors s’écrire comme:

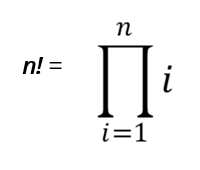
L’équation ci-dessus s’écrit selon la notation du produit pi, et aboutit à la relation récurrente vue ci-dessous:

n ! = n ∙ (n – 1) !.

On peut voir ci-dessous quelques exemples de cette notation :

• 4 ! = 4 ∙ 3!
• 7 ! = 7 ∙ 6!
• 80 ! = 80 ∙ 79 !, etc.

Tableau des factorielles

Le tableau ci-dessous donne un aperçu des factorielles pour les entiers compris entre 0 et 10:

Factorielle de 0 (zéro)

Il est largement connu que la factorielle de 0 est égale à 1 (un). Elle peut être dénotée comme:

0 ! = 1

Il existe plusieurs raisons pour justifier la notation et la définition stipulées ci-dessus. Tout d’abord, la définition fournit une autorisation pour une expression compacte d’un nombre considérable de formules, y compris la fonction exponentielle et la définition crée une extension de la relation de récurrence à 0.

En outre, lorsque n = 0, la définition de sa factorielle (n !) englobe le produit d’aucun nombre, ce qui signifie qu’elle est équivalente à l’identité multiplicative en termes plus larges.

De plus, la définition de la factorielle zéro ne comprend qu’une seule permutation de zéro ou d’aucun objet. Enfin, cette définition valide également un certain nombre d’identités en combinatoire.

Définitions à noter en relation avec la factorielle zéro

• Combinatoire : Un domaine des mathématiques qui se concentre sur le comptage.
• La permutation : En mathématiques, la permutation désigne l’arrangement des membres d’un ensemble dans un ordre ou une séquence linéaire.
• Relation de récurrence : La relation de récurrence, en mathématiques, fait référence à une équation qui définit une séquence ou un vaste ensemble de valeurs, de manière récursive. La récursion signifie définir quelque chose en termes d’elle-même.

Diverses applications de la fonction factorielle

La fonction factorielle peut être trouvée dans divers domaines des mathématiques. Tout d’abord, il existe n!es façons distinguées de ranger n objets spécifiques dans une séquence. Aussi, les factorielles peuvent être utilisées pour rendre compte de l’ignorance ou du non-respect de l’ordonnancement dans une formule, en servant de dénominateur.

Les factorielles se retrouvent également en algèbre via le théorème binomial et en calcul, où elles apparaissent dans les dénominateurs de la formule de Taylor. En outre, on peut trouver une factorielle dans les théories des probabilités et des nombres et elles peuvent être utilisées pour permettre la manipulation d’expressions.

Autres suites similaires à la factorielle

En mathématiques, il existe un certain nombre de suites comparables à la factorielle. Elles comprennent :

• Les factorielles doubles, qui sont utilisées pour simplifier les intégrales trigonométriques.
• Les factorielles multiples, qui peuvent être désignées par plusieurs points d’exclamation.
• Les primordiales, qui impliquent d’obtenir le produit des nombres premiers, inférieurs ou égaux à n.
• Les super-factorielles, qui se définissent comme le produit des n premières factorielles.
• Les hyper-factorielles, qui résultent de la multiplication d’un nombre de valeurs consécutives allant de 1 à n.

Ressources supplémentaires

L’ICFC est le fournisseur officiel de la certification mondiale Commercial Banking & Credit Analyst (CBCA)™CBCA™L’accréditation Commercial Banking & Credit Analyst (CBCA)™ est une norme mondiale pour les analystes de crédit qui couvre la finance, la comptabilité, l’analyse de crédit, l’analyse des flux de trésorerie, la modélisation des clauses restrictives, les remboursements de prêts, et plus encore. programme de certification, conçu pour aider quiconque à devenir un analyste financier de classe mondiale. Pour continuer à faire progresser votre carrière, les ressources supplémentaires de la FCI ci-dessous vous seront utiles :

• Matrice de corrélationMatrice de corrélationUne matrice de corrélation est simplement un tableau qui affiche les coefficients de corrélation de différentes variables. La matrice dépeint la corrélation entre toutes les paires de valeurs possibles dans un tableau. C’est un outil puissant pour résumer un grand ensemble de données et pour identifier et visualiser des modèles dans les données données.
• Mathématiques financièresMathématiques financièresLes mathématiques financières décrivent l’application des mathématiques et de la modélisation mathématique pour résoudre des problèmes financiers. elles sont parfois appelées
• QuantsQuantsLes analystes quantitatifs (également appelés « quants ») sont des professionnels spécialisés dans la conception, le développement et la mise en œuvre d’algorithmes et de modèles mathématiques ou statistiques destinés à résoudre des problèmes financiers complexes. Dans leur travail, les analystes quantitatifs appliquent un mélange de techniques et de connaissances
• Distribution standardDistribution d’échantillonnageUne distribution d’échantillonnage fait référence à une distribution de probabilité d’une statistique qui provient du choix d’échantillons aléatoires d’une population donnée

.