Formules mathématiques utiles pour le SAT
L’une des premières choses à faire lorsqu’on étudie la section mathématique du SAT est de mémoriser les formules. Si vous ne savez pas par où commencer, cette liste vous aidera.
Voici 9 formules de mathématiques du SAT qui vous seront utiles lors du test. Utilisez cette liste comme point de départ.
Apprenez à vous préparer aux tests standardisés avec nos cours de préparation au SAT et à l’ACT dispensés toute l’année dès aujourd’hui.
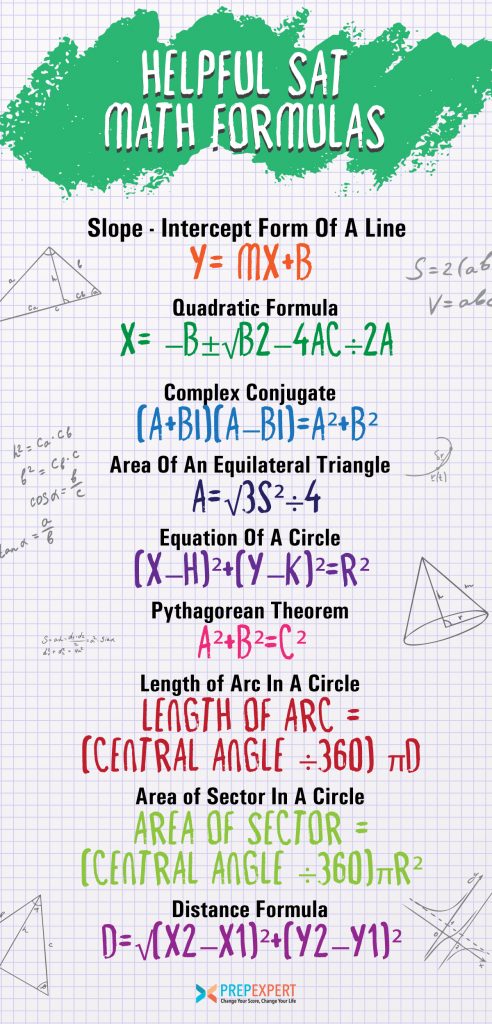
Forme pente-interception d’une droite
y=mx+b
« m » représente la pente de l’équation, « b » représente la valeur de l’ordonnée à l’origine. Par exemple, si nous avons l’équation y=3x+5, alors la pente est » 3 » et l’ordonnée à l’origine est (0,5).
Formule quadratique
x=-b±√b2-4ac÷2a
Avec cette formule, vous pouvez trouver les racines d’une équation quadratique si elle n’est pas facilement factorisable. Cependant, le quadratique doit être sous la forme y=ax2+bx+c.
À ce moment-là, branchez les coefficients et les constantes dans la formule. N’oubliez pas qu’en raison du ± au numérateur, vous aurez deux réponses distinctes.
Conjugué complexe
(a+bi)(a-bi)=a²+b²
La plupart des tests de mathématiques du SAT auront, au moins, une question qui nécessite de manipuler des nombres imaginaires. La formule du conjugué complexe vous permet d’annuler la partie imaginaire d’un nombre complexe. En conséquence, vous vous retrouverez avec un nombre réel.
Aire d’un triangle équilatéral
A=√3s²÷4
La formule de l’aire d’un triangle régulier est normalement fournie sur la feuille de référence du test, mais vous devez connaître la hauteur du triangle. Parfois, on ne vous fournira pas la hauteur et vous devrez la calculer.
La bonne nouvelle est que vous pouvez calculer l’aire d’un triangle équilatéral en branchant la longueur d’un de ses côtés dans cette formule. Vous pouvez sauter l’exigence de la hauteur !
Equation d’un cercle
(x-h)²+(y-k)²=r²
Normalement, une question de mathématiques du SAT nécessitera d’utiliser l’équation d’un cercle. Dans cette équation, les variables h et k représentent les coordonnées du centre du cercle et r
représente le rayon du cercle.
Théorème de Pythagore
a²+b²=c²
Le théorème de Pythagore s’applique aux triangles droits réguliers. Son but est de vous permettre de résoudre l’une des longueurs de côté inconnues étant donné n’importe quelle autre longueur de côté. a et b sont les jambes du triangle, et c est l’hypoténuse.
Longueur d’un arc dans un cercle
Longueur d’un arc = (angle central ÷360) πd
Les questions de géométrie ne sont pas fréquentes dans la section Mathématiques du SAT, mais vous aurez probablement toujours une question portant sur les arcs ou les secteurs dans un cercle. Un arc est une longueur entre deux points sur un cercle.
Ils sont généralement mesurés en prolongeant deux rayons à partir du centre du cercle avec un angle formé entre eux. Vous pouvez utiliser la mesure en degrés de cet arc en tant que fraction de 360, puis la multiplier par l’équation de la circonférence pour trouver la longueur de l’arc.
Aire du secteur dans un cercle
Aire du secteur = (angle central ÷360)πr²
Pas très différent d’un arc, le secteur d’un cercle est l’aire comprise entre deux rayons s’étendant depuis le centre. Visuellement, pensez-y comme une part de tarte essentiellement. Encore une fois, multipliez la mesure du degré comme une fraction de 360, puis multipliez-la par l’équation de l’aire d’un cercle pour trouver l’aire du secteur.
Formule de distance
d=√(x2-x1)²+(y2-y1)²
La formule de distance est fantastique pour déterminer rapidement la distance entre deux points. Pour l’utiliser, il suffit de prendre les valeurs des coordonnées et de les brancher pour trouver la distance. et assurez-vous d’appliquer les carrés et la racine carrée à la bonne étape.
Pour plus de conseils sur la stratégie des tests, les admissions à l’université et les demandes de bourses, inscrivez-vous à notre classe GRATUITE qui se déroule en ce moment !