La corrélation en statistique : L’analyse de corrélation expliquée

Contenu :
Qu’est-ce que la corrélation ?
Le coefficient de corrélation
Corrélation dans Excel

Définition

La corrélation est utilisée pour tester les relations entre des variables quantitatives ou des variables catégorielles. En d’autres termes, c’est une mesure de la façon dont les choses sont liées. L’étude de la corrélation entre les variables est appelée analyse de corrélation.

Quelques exemples de données qui ont une corrélation élevée :

• Votre apport calorique et votre poids.
• Votre couleur des yeux et celle de vos proches.
• Le temps que vous passez à étudier et votre moyenne générale.

Des exemples de données qui ont une faible corrélation (ou pas du tout):

• Votre préférence sexuelle et le type de céréales que vous mangez.
• Le nom d’un chien et le type de biscuit pour chien qu’il préfère.
• Le coût d’un lavage de voiture et le temps qu’il faut pour acheter un soda à l’intérieur de la station.

Les corrélations sont utiles car si vous pouvez trouver quelle relation ont les variables, vous pouvez faire des prédictions sur le comportement futur. Savoir ce que l’avenir réserve est très important dans les sciences sociales comme le gouvernement et les soins de santé. Les entreprises utilisent également ces statistiques pour les budgets et les plans d’affaires.

Le coefficient de corrélation

Un coefficient de corrélation est un moyen de mettre une valeur à la relation. Les coefficients de corrélation ont une valeur comprise entre -1 et 1. Un  » 0  » signifie qu’il n’y a pas du tout de relation entre les variables, tandis que -1 ou 1 signifie qu’il y a une corrélation négative ou positive parfaite (la corrélation négative ou positive fait ici référence au type de graphique que la relation produira).

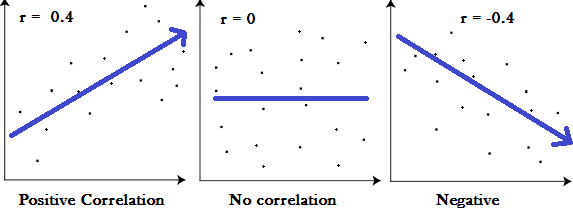
Graphes montrant une corrélation de -1, 0 et +1

Types

Le coefficient de corrélation le plus courant est le coefficient de corrélation de Pearson. Il est utilisé pour tester les relations linéaires entre les données. En stats AP ou en stats élémentaires, le Pearson est probablement le seul avec lequel vous travaillerez. Cependant, vous pouvez en rencontrer d’autres, en fonction du type de données sur lesquelles vous travaillez. Par exemple, le coefficient lambda de Goodman et Kruskal est un coefficient assez courant. Il peut être symétrique, où vous n’avez pas à préciser quelle variable est dépendante, et asymétrique où la variable dépendante est spécifiée.

Corrélation dans Excel

Trouver les coefficients de corrélation de Pearson à la main est laid et implique beaucoup de longs calculs mathématiques. Cependant, Excel peut effectuer ces calculs pour vous en une fraction de seconde. Deux options s’offrent à vous dans Excel (2013 et versions ultérieures) : La fonction CORREL ou le Data Analysis Toolpak.

Si vous êtes familier avec la saisie de fonctions dans Excel, vous pourriez saisir la commande CORREL:
=CORREL(tableau 1, tableau 2)
Par exemple, =CORREL(A2 :A6,B2:B6)

Cependant, le Data Analysis Toolpak est beaucoup plus facile dans l’ensemble, car vous n’avez pas à vous souvenir (ou à chercher) un tableau de fonctions ; Elles sont toutes simplement listées dans la liste Data Analysis. Si l’Analyse de données n’apparaît pas à l’extrême droite de l’onglet Données, vérifiez que vous avez chargé le Data Analysis Toolpak. Le Data Analysis Toolpak est un complément optionnel d’Excel qui vous donne accès à de nombreuses fonctions, notamment :

• Corrélation,
• Régression linéaire,
• Histogrammes,
• Tests T,
• Tests Z
• Tests ANOVA à une voie et à deux voies.

Étape 1 : Tapez vos données dans une feuille de calcul dans Excel. Le meilleur format est en deux colonnes. Placez vos valeurs x dans la colonne A et vos valeurs y dans la colonne B.

Étape 2 : Cliquez sur l’onglet « Données », puis sur « Analyse des données ».

Étape 3 : Cliquez sur « Corrélation », puis cliquez sur « OK ».

Étape 4 : Tapez l’emplacement de vos variables x-y dans la case Input
Range. Ou bien, utilisez votre curseur pour mettre en surbrillance la zone où se trouvent vos variables.

Étape 5 : Cliquez sur l’option  » colonnes  » ou  » lignes  » pour indiquer à Excel comment vos données sont disposées. Dans la plupart des cas, vous cliquerez sur  » colonnes  » car c’est la façon standard de disposer les données dans Excel.

Étape 6 : Cochez l’option  » Étiquettes de la première ligne  » si vous avez des en-têtes de colonne.

Étape 7 : Cliquez sur la zone de texte  » Plage de sortie « , puis sélectionnez une zone de la feuille de calcul où vous voulez que votre sortie aille.

C’est tout !

Voyez notre chaîne YouTube pour plus de conseils et d’aide sur Excel !

Agresti A. (1990) Analyse des données catégorielles. John Wiley and Sons, New York.
Dodge, Y. (2008). L’encyclopédie concise de la statistique. Springer.
Vogt, W.P. (2005). Dictionnaire des statistiques & Méthodologie : Un guide non technique pour les sciences sociales. SAGE.
Wheelan, C. (2014). Naked Statistics. W. W. Norton & Société

——————————————————————————

Vous avez besoin d’aide pour un devoir ou une question de test ? Avec Chegg Study, vous pouvez obtenir des solutions étape par étape à vos questions de la part d’un expert dans le domaine. Vos 30 premières minutes avec un tuteur Chegg sont gratuites !