Le juste milieu : une grande découverte ou un phénomène naturel ?

Qu’ont en commun les façades de la National Gallery de Trafalgar Square à Londres et de l’Opéra de Sydney en Australie ?

La plupart des gens suggéreraient que les deux bâtiments ont peu de similitudes – le premier est symétrique et de proportion classique, tandis que le second est moderne, organique et curviligne.

Un architecte pourrait offrir la réponse provocante que les deux bâtiments présentent des compositions de formes géométriques, combinant cercles, carrés et rectangles. Mais cette réponse n’est pas la raison pour laquelle les deux sont liés dans la culture populaire.

Au contraire, on les retrouve sur les listes de bâtiments qui s’appuient prétendument sur le nombre d’or, décrit ci-dessous, pour obtenir une composition esthétique parfaite.

Le nombre d’or – également connu sous le nom de section d’or ou de proportion divine – est un concept mathématique qui remonte généralement au 15e siècle, une période où la géométrie servait à la fois des objectifs pratiques et symboliques.

C’est un rapport qui définit une relation récurrente entre un élément plus grand et un sous-ensemble plus petit de cet élément.

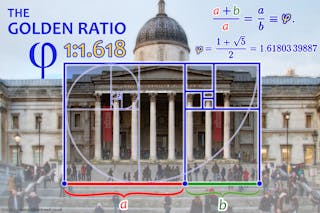
En termes mathématiques simples, si une ligne ab est divisée par un point C, de telle sorte que le rapport de la ligne entière (AB) au segment le plus long (AC) est égal au rapport du segment le plus long (AC) au segment le plus petit (CB), alors le rapport AB : AC (et, bien sûr, le rapport du sous-ensemble AC : CB) est connu comme le nombre d’or (φ ou « phi »).

Donc, par exemple, si la longueur de la ligne de départ AB est de 1,000, alors le Nombre d’Or est approximativement de 1,618.

Lorsque le Nombre d’Or est conceptualisé en deux dimensions, il est typiquement présenté comme une spirale régulière qui est définie par une série de carrés et d’arcs, chacun formant des « Rectangles d’Or ».

Utilisé par les architectes de l’Antiquité

Il est prouvé que les architectes égyptiens, romains et grecs de l’Antiquité étaient capables de produire ce ratio à l’aide d’outils simples et, comme leurs homologues du XVe siècle, ils ont pu le considérer comme ayant une signification figurative plus importante.

Ce potentiel symbolique découle de la façon dont la forme en spirale du moyen ressemble aux modèles de croissance observés dans la nature et ses proportions rappellent celles des corps humains. Ainsi, ces spirales et rectangles simples, qui servaient à suggérer la présence d’un ordre universel sous-jacent au monde, étaient de ce fait surnommés « dorés » ou « divins ».

Pour l’architecte antique, le rectangle d’or devait offrir une recette pour créer des bâtiments faciles à dessiner, agréables à l’œil et, surtout, pouvant être justifiés par le fait qu’ils représentaient un lien avec dieu ou l’univers.

À une époque où, pour l’architecte, la décapitation était un risque plus courant que le litige, le nombre d’or offrait un type spécial d’indemnité.

Toutefois, alors que la plupart des symboles du monde antique ont aujourd’hui perdu leur pouvoir, le nombre d’or fait toujours l’objet d’un culte, avec plusieurs centaines de sites web montrant sa forme en spirale superposée à des tournesols, des coquillages, des peintures célèbres et des visages d’acteurs populaires. Le culte contemporain du juste milieu présente ces superpositions comme la preuve du secret caché de l’univers.

Le problème avec de telles affirmations est que les chercheurs ont démontré à plusieurs reprises que le nombre d’or n’est pas une proportion universellement attrayante et qu’il n’est pas statistiquement significatif dans la nature ou dans le corps humain. Mais le fait que ses propriétés plus mystiques aient été réfutées de manière exhaustive ne doit pas servir à reléguer cette théorie dans la catégorie de l’ésotérisme.

Géométrie naturelle

Comme tous les ratios esthétiques (le « Modulor » de Le Corbusier et le « Nombre plastique » de van der Laan sont tout aussi dignes d’intérêt), sa large application dans le design apporte un degré d’ordre et de cohérence à une œuvre, quelque chose d’important en architecture car un bâtiment est rarement vécu d’une seule distance.

En utilisant n’importe lequel de ces rapports, un architecte peut concevoir une poignée de porte qui a une relation complémentaire avec sa porte, qui à son tour a une relation similaire avec son mur d’enceinte, et ainsi de suite. Les systèmes proportionnels sont utiles à cette fin, mais leur présence, même dans un grand bâtiment, ne doit pas être considérée comme particulièrement significative.

Dans les années 1980, des expériences ont été menées dans lesquelles des enfants ont reçu des règles et des paires de compas et ont été encouragés à dessiner des formes. Les premiers cercles et carrés n’ont pas tardé à apparaître, puis des triangles, des grilles et des arcs, et avant la fin de la première heure, des rectangles d’or ont commencé à apparaître.

Est-ce que cela implique que le nombre d’or est inscrit dans le subconscient de chaque enfant ou est-ce simplement une forme qui surgit naturellement de l’utilisation de cet ensemble particulier d’outils ?

On se souvient que la National Gallery et l’Opéra de Sydney – mentionnés au début de cet article – sont tous deux des compositions de rectangles et d’arcs, dessinés dans les deux cas par des architectes à l’aide d’une règle et d’une paire de compas. Ils ont également été dessinés par des architectes (respectivement William Wilkins et Jørn Utzon) qui étaient conscients de la tradition classique et de ses tropes géométriques.

Pour ces deux raisons, la présence de quelque chose se rapprochant vaguement d’un juste milieu ne doit pas être considérée comme une grande découverte, mais elle pourrait être le signe que l’architecte a été formé à apprécier la nécessité d’une cohérence au sein d’un design.