Mesures du temps : biennium, lustrum, décennie, siècle, millénaire

Dans ce billet, nous allons voir les mesures du temps qui font référence à des quantités d’années : biennium, lustrum, décennie, siècle, millénaire

Si vous voulez revoir les précédents billets sur les unités de temps, vous pouvez le faire ici :

• Apprendre comment mesurer le temps et les unités associées
• Temps : concepts de base pour apprendre à lire l’heure
• Problèmes de mesure du temps : formes simples et complexes

Avant de poursuivre votre lecture, la chose la plus importante que vous devez comprendre est la suivante :

Nous allons mettre en pratique ces concepts à l’aide de quelques problèmes que vous pouvez trouver lors de vos sessions quotidiennes de Smartick. Commençons !

Problème 1

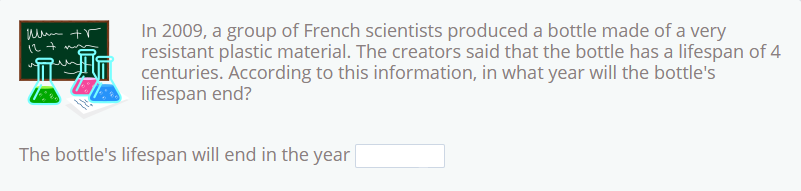
Pour résoudre ce problème, nous devons nous rappeler qu’un siècle vaut 100 ans, donc 4 siècles font 4×100=400 ans.

Sachant cela, il suffit d’ajouter ces 400 ans à l’année de fabrication de la bouteille, 2009.

Donc 2009 + 400 = 2409

Réponse : La durée de vie de la bouteille se terminera en 2409

Problème 2

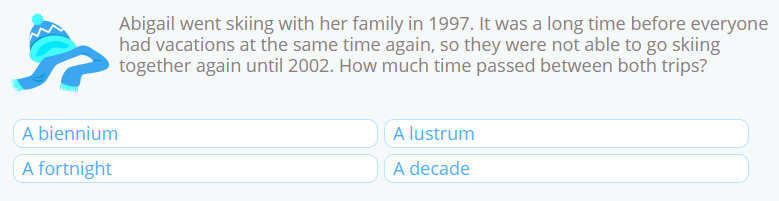
Pour résoudre ce problème, il faut soustraire les dates.

2002 – 1997 = 5

L’unité de temps équivalente à 5 ans est un lustrum.

Réponse : Un lustrum est passé entre les deux voyages

Problème 3

La première chose que nous devons faire pour résoudre ce problème est de calculer le nombre d’années qui s’écoulent entre 3655 av. J.-C. et 2010.

Pour ce faire, nous additionnons 3655 et 2010. 3655 + 2010 = 5665

Maintenant, nous devons décomposer cette durée en unités plus petites.

5000 ans, c’est 5 millénaires

600 ans, c’est 6 siècles

60 ans, c’est 6 décennies

5 ans, c’est un lustrum

Donc, 5 millénaires + 6 siècles + 6 décennies + un lustrum

Réponse : 5 millénaires, 6 siècles, 6 décennies et un lustrum s’étaient écoulés

Problème 4

Pour résoudre ce problème, il faut d’abord tenir compte du fait que la roche a maintenant 1/4 de sa taille initiale, ce qui signifie qu’elle a perdu 3/4 de sa taille.

Si 13 lustra passent pour chaque quart, nous devons multiplier cette quantité par 3. 3 x 13 = 39 lustra

Il ne nous reste plus qu’à multiplier les 39 lustra par les 5 années que contient chaque lustrum :

39 x 5 = 195

Réponse : Il a été exposé à 195 années d’érosion

J’espère que ces exercices vous ont aidé à comprendre des unités de temps plus grandes. N’oubliez pas que si vous voulez pratiquer davantage de ces problèmes, inscrivez-vous sur Smartick et faites votre séance tous les jours.

En savoir plus :

• Apprenez à résoudre un problème de mot de temps
• Comment résoudre des problèmes de conversion de masse
• Problèmes de mesure du temps : Formes simples et complexes
• Comment résoudre un problème de soustraction avec regroupement
• Soustraction avec emprunt : Une explication de deux algorithmes différents

• Auteur
• Messages récents

Équipe de création de contenu.
Une équipe multidisciplinaire et multiculturelle composée de mathématiciens, d’enseignants, de professeurs et d’autres professionnels de l’éducation !
Ils s’efforcent de créer le meilleur contenu mathématique possible.

Derniers messages de Smartick (voir tous)

• Angles intérieurs consécutifs : Ce qu’ils sont et comment les trouver avec des exemples – 03/11/2021
• Des exemples de problèmes de mots de deuxième année avec des solutions – 02/04/2021
• Qu’est-ce qu’un angle obtus ? – 15/01/2021

.