Quel est le plus grand nombre ?

Les nombres sont infinis – mais sur le chemin de l’infini, il y a des bornes assez éloignées.

Pour nos ancêtres, un million était le plus grand des nombres nécessaires. Il n’était pas nécessaire d’invoquer les milliards (1 000 000 000) de la finance ou les téraoctets (1012) de l’informatique. La technologie nous a rendus blasés de l’utilisation de nombres à 9 ou 12 chiffres dans la conversation. Cependant, il y a encore un long chemin à parcourir avant même de rattraper l’échelle de notre place dans l’univers, sans parler des nombres vertigineusement gigantesques imaginés par les mathématiciens.

Nombres standards

Au delà d’un milliard – l’ordre de grandeur de la population humaine – il faut vraiment dire adieu à l’idée d’avoir des noms pour les nombres. (Bien qu’ils existent jusqu’à 1063, ils ne sont pas d’usage courant). Pour la distance parcourue par la lumière en une minute, le nombre d’atomes dans un gramme de carbone ou la distance entre les galaxies, les scientifiques utilisent la forme standard pour s’exprimer. La forme standard enregistre tous les nombres au format a × 10n, où a est un nombre compris entre 1 et 10 et n peut être un nombre quelconque. C’est ce que vous utiliseriez pour parler du nombre d’atomes de carbone dans un échantillon de 12 g. Ce qui, soit dit en passant, est 6,22 × 1023, le nombre d’Avogadro, et est assez grand. L’univers observable fait environ 8,8 × 1023 km de large, et on estime qu’il contient 1087 particules. Mais plus grands que ces chiffres, et de loin, sont les constructions des esprits mathématiques.

Let me googol it for you

Immortalisé dans l’usage courant par le géant de l’internet, un googol est le nombre 10100 – 10, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000. Le mathématicien américain Edward Kasner a demandé à son neveu Milton de lui donner un nom, et il est devenu un googol. Mais le prochain grand nombre est le googolplex, qui élève 10 à la puissance d’un googol. C’est astronomiquement plus grand qu’un googol – il est impossible d’écrire un googolplex en notation standard même si vous écriviez un seul chiffre sur chaque particule de l’univers.

La puissance des puissances

Ajouter une exponentielle dans l’exposant augmente vraiment le taux d’agrandissement des nombres.

3×3×3=27

3(33) = 7 625 597 484 987

Naturellement, dans une quête de nombres plus grands, on ajouterait de plus en plus de puissances à la tour. Mais cela devient rapidement gênant à écrire, en plus d’aboutir à des tours qui font paraître celle de Pise stable. Le changement de notation permet de condenser ces tours et d’exprimer des concepts plus élevés.

Suivre les flèches

Développer une autre façon de dénoter les puissances :

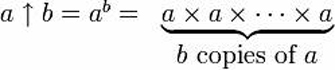
Donald Knuth a inventé un nouvel opérateur d’exponentiation répétée (« tetration »), pour faire redescendre sur terre ces tours de puissance.

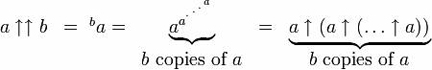
En utilisation, la double flèche ressemble à ceci :

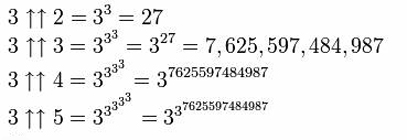
On peut encore l’étendre en ajoutant une troisième flèche, créant ainsi l’opération de  » pentation  » – tétration répétée.

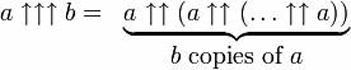
En mots, cela implique de tétrader a au a (donc, une tour de puissance de a ‘a), puis de construire une autre tour de ‘a aussi haute que cette tour de puissance, puis d’utiliser le résultat de cette tour de puissance pour déterminer le nombre de ‘a’ dans la suivante – ce qui aboutit au calcul de b tours de puissance, dont la hauteur augmente en fonction du résultat de la tétration précédente.

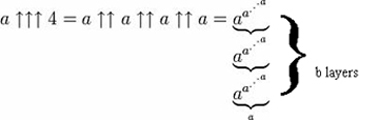
Et on peut encore ajouter d’autres flèches, même si réfléchir aux opérations qu’elles dénotent peut demander plus de temps de cerveau que vous n’êtes prêt à consacrer à la question. Mais armés de cette notation, nous pouvons maintenant reconnaître de véritables grands nombres.

Appeler Ackermann et Graham

Les preuves mathématiques nous ont donné des quantités massives. Au début du vingtième siècle, les mathématiciens voulaient savoir comment dire si une séquence était calculable – pouvait-on définir un processus mécanique pour l’élaborer ? Il a été proposé qu’une séquence soit calculable si elle avait la propriété d’être « récursive primitive ». Wilhelm Ackermann a jeté un pavé dans la mare en inventant une séquence qui, bien que calculable, n’était pas récursive primitive. Et cela donne ceci :

Commencez par l’opération mathématique la plus simple possible – l’addition. Appliquez-la au premier nombre naturel, 1:

1 + 1 = 2

Puis passez à l’opération suivante, la multiplication (addition répétée). Faites-le pour le nombre suivant :

2 × 2 = 4

La prochaine étape est la multiplication répétée – l’exponentiation pour vous et moi – avec 3 comme variable.

33 = 27

Pour l’instant, si chétif. Mais nous venons de définir une fonction d’exponentiation répétée, la tétrade, et si nous faisons cela à 4…

Il a l’air petit, il a 10154 chiffres. Et ce n’est que le 4e terme de la séquence.

Le cinquième est … une tour de puissance de cinq chiffres de haut.

Le sixième est . Cinq symboles seulement dénotent un nombre plus grand qu’il n’y a de place dans l’univers, même si vous écriviez chaque chiffre dans une police de 1nm de large. Et la séquence continue.

La même notation en flèche vers le haut a été utilisée par Ronald Graham pour limiter certaines propriétés d’un hypercube (un cube en 4 dimensions spatiales), bien que le  » nombre de Graham  » soit maintenant plus connu simplement pour être collossal.

Le nombre de Graham est défini comme suit :

Le nombre de flèches dans chaque couche est donné par le résultat de l’évaluation des flèches de la couche inférieure, jusqu’à atteindre le nombre final après 64 couches. Pour vous donner une idée de la taille de tout cela, nous pouvons examiner la première couche seule :

où le nombre de trois dans l’expression de droite est

Maintenant chaque opération de tétrapénie () se réduit à une « tour » d’exponentiations (). selon la définition

où il y a X trois.

Donc,

où le nombre de trois est , devient, uniquement en termes de « tours d’exponentiation » répétées, et où le nombre de trois dans chaque tour, en partant de la tour la plus à gauche, est spécifié par la valeur de la tour suivante à droite.

C’est, techniquement parlant, beaucoup de trois. Ne vous détendez pas pour autant, car le nombre de Graham, bien qu’étant le plus grand nombre que les mathématiciens aient encore eu besoin d’écrire explicitement, est éclipsé par certains produits de la théorie de l’informatique. Nous n’avons pas la place de les détailler ici, mais si le nombre de Graham ne vous suffit pas, consultez l’article de Scott Aaronson intitulé « Qui peut écrire le plus grand nombre ? Il revient également plus en détail sur l’histoire des grands nombres et leurs explications.

Gros, plus gros, plus gros

Le monde des nombres est, comme on peut s’y attendre, infini. La nature est assez grande, mais les nombres qu’elle nous demande d’utiliser sont bien plus petits que ceux que les mathématiciens humains ont imaginés. En ce sens, l’esprit humain est plus grand que l’univers.