Sélectionner le meilleur algorithme d’apprentissage automatique pour votre problème de régression

J’ai récemment lancé une lettre d’information éducative axée sur le livre-bulletin d’information éducatif axé sur les livres. Book Dives est une lettre d’information bihebdomadaire où, pour chaque nouveau numéro, nous nous plongeons dans un livre non fictionnel. Vous apprendrez les leçons essentielles du livre et comment les appliquer dans la vie réelle. Vous pouvez vous y abonner ici.
Lorsqu’on aborde n’importe quel type de problème d’apprentissage machine (ML), il existe de nombreux algorithmes différents parmi lesquels choisir. Dans le domaine de l’apprentissage automatique, il existe un théorème appelé « No Free Lunch », qui stipule qu’aucun algorithme d’apprentissage automatique n’est le meilleur pour tous les problèmes. Les performances des différents algorithmes ML dépendent fortement de la taille et de la structure de vos données. Ainsi, le choix correct de l’algorithme reste souvent flou, à moins que nous ne testions directement nos algorithmes par le biais de simples essais et erreurs.
Mais, il existe des avantages et des inconvénients pour chaque algorithme ML que nous pouvons utiliser comme guide. Même si un algorithme ne sera pas toujours meilleur qu’un autre, il existe certaines propriétés de chaque algorithme que nous pouvons utiliser comme guide pour sélectionner rapidement le bon et régler les hyper paramètres. Nous allons examiner quelques algorithmes ML importants pour les problèmes de régression et établir des directives pour savoir quand les utiliser en fonction de leurs forces et de leurs faiblesses. Ce post devrait alors servir de grande aide pour sélectionner le meilleur algorithme ML pour votre problème de régression !
Juste avant de nous lancer, consultez la newsletter AI Smart pour lire les dernières et les meilleures informations sur l’IA, l’apprentissage automatique et la science des données !
Régression linéaire et polynomiale
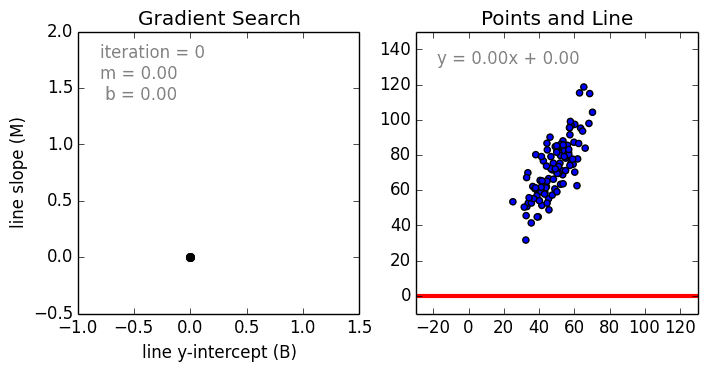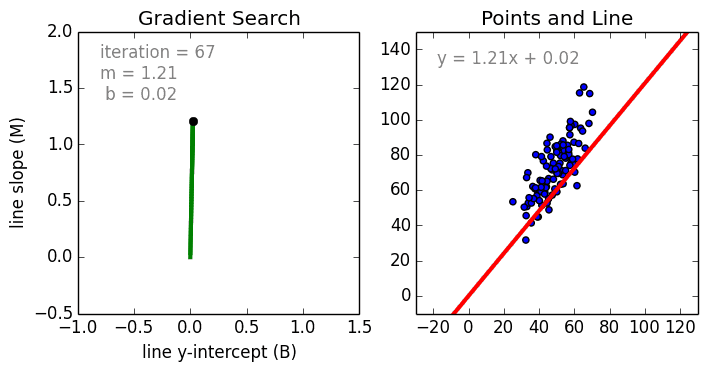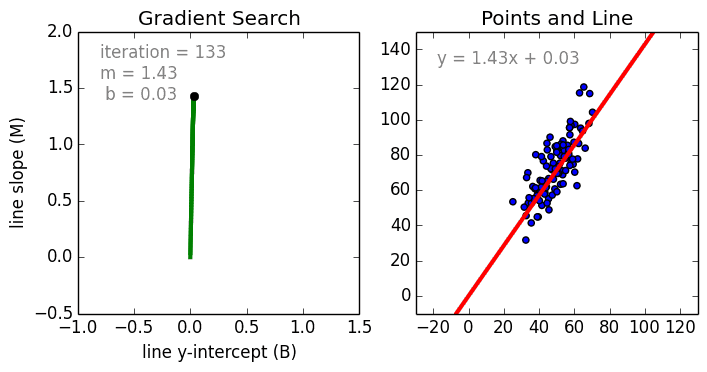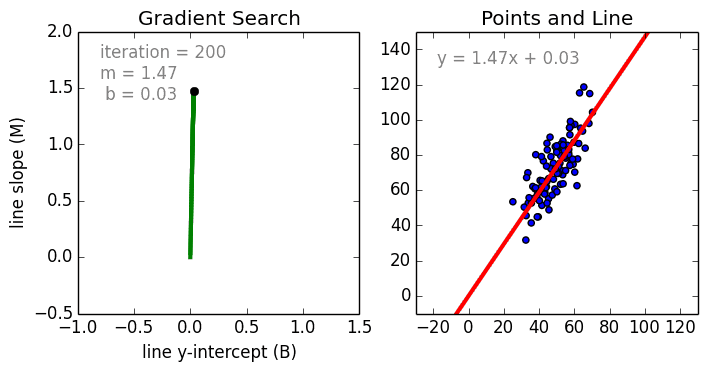
Commençons par le cas simple, La régression linéaire à une variable est une technique utilisée pour modéliser la relation entre une seule variable indépendante d’entrée (variable caractéristique) et une variable dépendante de sortie en utilisant un modèle linéaire, c’est-à-dire une ligne.c’est-à-dire une ligne. Dans le cas plus général de la régression linéaire multi-variable, un modèle est créé pour la relation entre plusieurs variables indépendantes en entrée (variables caractéristiques) et une variable dépendante en sortie. Le modèle reste linéaire en ce sens que la sortie est une combinaison linéaire des variables d’entrée.
Il existe un troisième cas plus général appelé Régression polynomiale où le modèle devient maintenant une combinaison non linéaire des variables caractéristiques c’est-à-dire qu’il peut y avoir des variables exponentielles, sinus et cosinus, etc. Cela nécessite toutefois de savoir comment les données sont liées à la sortie. Les modèles de régression peuvent être formés en utilisant la descente de gradient stochastique (SGD).
Pros:
- Rapide à modéliser et est particulièrement utile lorsque la relation à modéliser n’est pas extrêmement complexe et si vous n’avez pas beaucoup de données.
- La régression linéaire est simple à comprendre, ce qui peut être très précieux pour les décisions commerciales.
Cons:
- Pour les données non linéaires, la régression polynomiale peut être assez difficile à concevoir, car il faut avoir certaines informations sur la structure des données et la relation entre les variables caractéristiques.
- En conséquence de ce qui précède, ces modèles ne sont pas aussi bons que les autres lorsqu’il s’agit de données très complexes.
Réseaux neuronaux
.
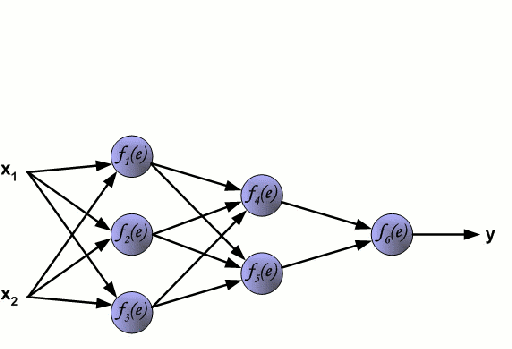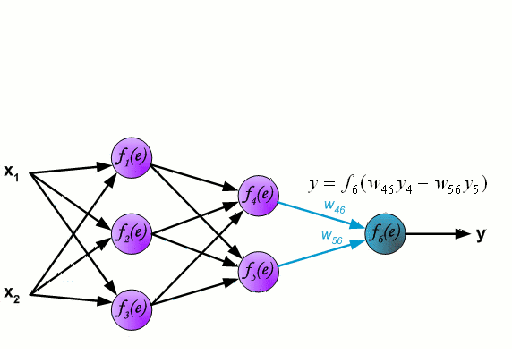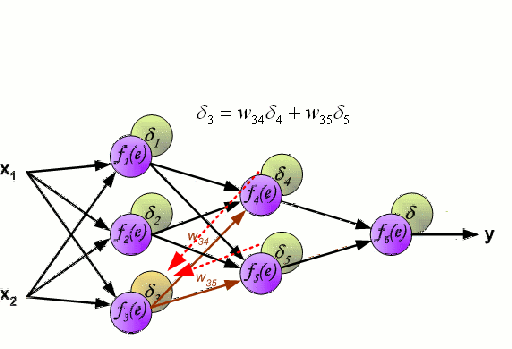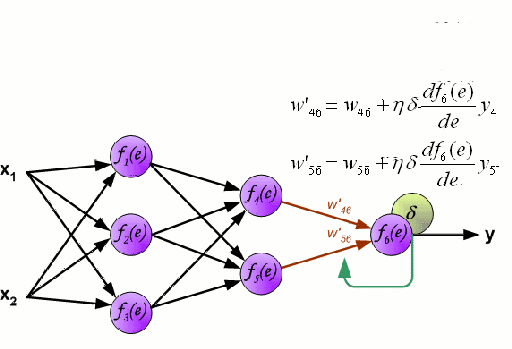
Un réseau neuronal est constitué d’un groupe interconnecté de nœuds appelés neurones. Les variables caractéristiques d’entrée provenant des données sont transmises à ces neurones sous la forme d’une combinaison linéaire multi-variable, où les valeurs multipliées par chaque variable caractéristique sont appelées poids. Une non-linéarité est ensuite appliquée à cette combinaison linéaire, ce qui donne au réseau neuronal la capacité de modéliser des relations non linéaires complexes. Un réseau neuronal peut comporter plusieurs couches, la sortie d’une couche étant transmise de la même manière à la couche suivante. À la sortie, il n’y a généralement pas de non-linéarité appliquée. Les réseaux neuronaux sont formés à l’aide de la descente de gradient stochastique (SGD) et de l’algorithme de rétropropagation (tous deux affichés dans le GIF ci-dessus).
Pros:
- Puisque les réseaux neuronaux peuvent avoir de nombreuses couches (et donc des paramètres) avec des non-linéarités, ils sont très efficaces pour modéliser des relations non linéaires très complexes.
- Nous n’avons généralement pas à nous préoccuper de la structure des données à les réseaux neuronaux sont très flexibles dans l’apprentissage de presque n’importe quel type de relations variables caractéristiques.
- La recherche a constamment montré que le simple fait de donner au réseau plus de données d’entraînement, qu’elles soient totalement nouvelles ou qu’elles proviennent de l’augmentation de l’ensemble de données d’origine, améliore les performances du réseau.
Les inconvénients:
- En raison de la complexité de ces modèles, ils ne sont pas faciles à interpréter et à comprendre.
- Ils peuvent être assez difficiles et exigeants en termes de calcul pour l’entraînement, nécessitant un réglage minutieux des hyperparamètres et le paramétrage du calendrier du taux d’apprentissage.
- Ils nécessitent beaucoup de données pour atteindre des performances élevées et sont généralement surpassés par d’autres algorithmes ML dans les cas de « petites données ».
Arbres de régression et forêts aléatoires
.
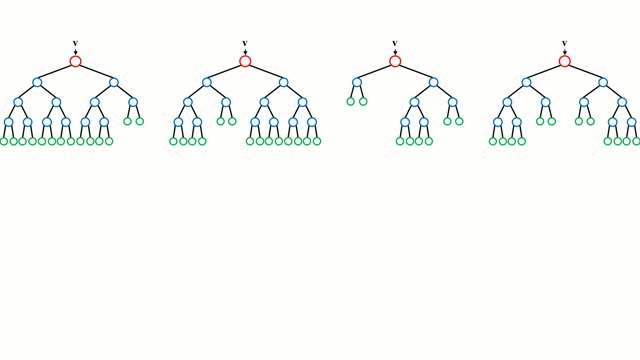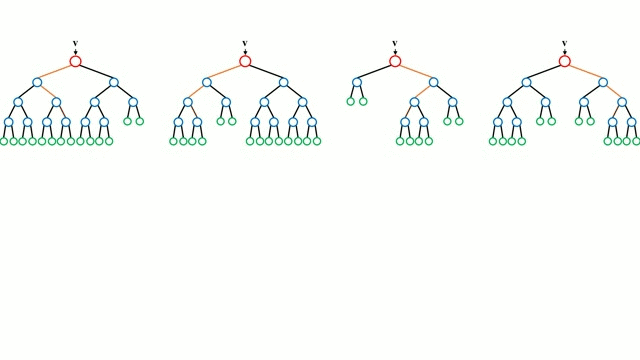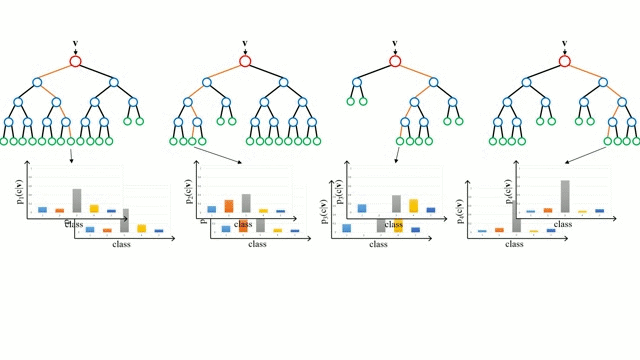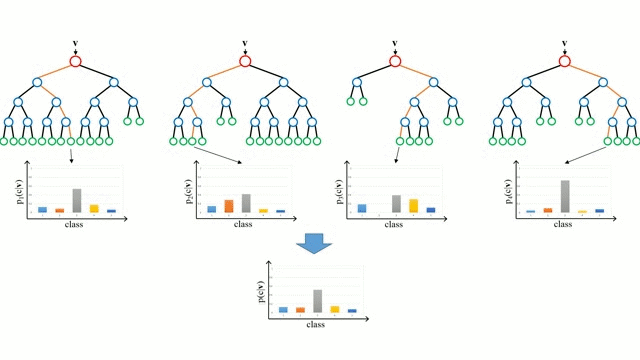
En commençant par le cas de base, un arbre de décision est un modèle intuitif où l’on parcourt les branches de l’arbre et où l’on choisit la prochaine branche à descendre en fonction d’une décision prise à un nœud. L’induction d’arbre est la tâche qui consiste à prendre un ensemble d’instances de formation en entrée, à décider quels sont les meilleurs attributs pour les diviser, à diviser l’ensemble de données et à répéter sur les ensembles de données divisées résultantes jusqu’à ce que toutes les instances de formation soient catégorisées. Lors de la construction de l’arbre, l’objectif est de diviser sur les attributs qui créent les nœuds enfants les plus purs possibles, ce qui réduirait au minimum le nombre de divisions nécessaires pour classer toutes les instances de notre jeu de données. La pureté est mesurée par le concept de gain d’information, qui se rapporte à ce qu’il faudrait savoir sur une instance précédemment non vue pour qu’elle soit correctement classée. En pratique, cela se mesure en comparant l’entropie, ou la quantité d’informations nécessaires pour classer une instance unique d’une partition actuelle de l’ensemble de données, à la quantité d’informations nécessaires pour classer une instance unique si la partition actuelle de l’ensemble de données devait être davantage partitionnée sur un attribut donné.
Les forêts aléatoires sont simplement un ensemble d’arbres de décision. Le vecteur d’entrée est parcouru par plusieurs arbres de décision. Pour la régression, la valeur de sortie de tous les arbres est moyennée ; pour la classification, un schéma de vote est utilisé pour déterminer la classe finale.
Pros:
- Génial pour apprendre des relations complexes et hautement non linéaires. Ils peuvent généralement atteindre des performances assez élevées, meilleures que la régression polynomiale et souvent à égalité avec les réseaux neuronaux.
- Très facile à interpréter et à comprendre. Bien que le modèle final formé puisse apprendre des relations complexes, les frontières de décision qui sont construites pendant la formation sont faciles et pratiques à comprendre.
Cons:
- En raison de la nature de la formation des arbres de décision, ils peuvent être enclins à un surajustement majeur. Un modèle d’arbre de décision terminé peut être trop complexe et contenir une structure inutile. Bien que cela puisse parfois être atténué en utilisant un élagage approprié des arbres et de plus grands ensembles de forêts aléatoires.
- L’utilisation de plus grands ensembles de forêts aléatoires pour obtenir de meilleures performances s’accompagne des inconvénients d’être plus lent et de nécessiter plus de mémoire.
Conclusion
Boom ! Voilà vos avantages et vos inconvénients ! Dans le prochain post, nous allons examiner les avantages et les inconvénients des différents modèles de classification. J’espère que vous avez apprécié ce post et que vous avez appris quelque chose de nouveau et d’utile. Si c’est le cas, n’hésitez pas à lui donner quelques applaudissements.