Équations de flambement des colonnes et comportement de flambement | DegreeTutors.com

Dans le dernier post de cette série, nous avons introduit quelques concepts de base en utilisant une structure idéalisée simplifiée. Dans ce post, nous allons commencer à considérer des structures plus réalistes et déterminer les équations de flambement des colonnes. En particulier, nous déterminerons une expression pour la charge critique d’un poteau chargé axialement avec des extrémités goupillées. Puis nous explorerons d’autres conditions de support.

📓 Ce post est la deuxième partie d’une série de trois parties sur le flambement des colonnes. Vous pouvez télécharger gratuitement la série complète en trois parties, joliment formatée et tapée dans un ebook.

Nous allons couvrir pas mal de choses dans celui-ci, alors voici une table des matières…

Des colonnes épinglées aux deux extrémités
- Établir l’équation différentielle
- Résoudre l’équation différentielle
- Résoudre les constantes d’intégration
Modes de flambement et formes de mode
- Flexion maximale sous charge critique
- Modes de flambement d’ordre supérieur
Colonnes avec d’autres conditions d’appui
- Fixe-.Fixe
- Fixe-libre
- Fixe-épinglé

Axe de flambement

Contrainte critique
Longueur effective de la colonne

Lorsque l’on fait référence à un appui épinglé, il s’agit d’un support qui n’offre aucune résistance à la rotation. Parfois, nous rencontrons dans la pratique des supports de goupilles qui se rapprochent très fortement de cette définition théorique. En voici quelques exemples :

Pour les besoins de notre discussion ici, nous supposerons que nous avons affaire à des supports de broches comme ceux-ci, et qu’ils n’empêchent pas la rotation de la structure.

1.0 Equation de flambement pour des colonnes goupillées aux deux extrémités

Pour analyser cette structure, nous allons utiliser l’équation différentielle de la courbe de défection dans laquelle est le moment de flexion interne à une section donnée, représente la déformation latérale de la colonne et la distance sur la longueur de la colonne. est appelée la rigidité en flexion et est le produit du module de Young et du deuxième moment de l’aire de la section transversale .

$\begin{align*}EI\frac{\mathrm{d}^2v}{\mathrm{dx^2}}=M\end{align*}$

💡Cette équation modélise simplement la forme déviée du poteau pour une rigidité en flexion donnée.

Vous avez probablement rencontré cette équation ailleurs dans vos études d’ingénieur. Notre colonne déviée latéralement se comporte à peu près de la même manière qu’une poutre. Rappelez-vous que le flambement est une rupture par flexion plutôt qu’une rupture due à une compression directe (écrasement). Notre tâche maintenant, est d’utiliser cette équation pour dériver une expression pour la charge axiale critique dans une colonne à extrémité goupillée.

📌 Tout comme pour la structure idéalisée discutée dans le post précédent, notre dérivation ici supposera également que toutes les déflexions sont petites par rapport à la taille de la structure.

Établissement de l’équation différentielle

Premièrement, considérons la structure, sa forme défléchie et le diagramme en corps librediagramme de corps libre qui résulte de la coupe de la structure à une distance du support inférieur…

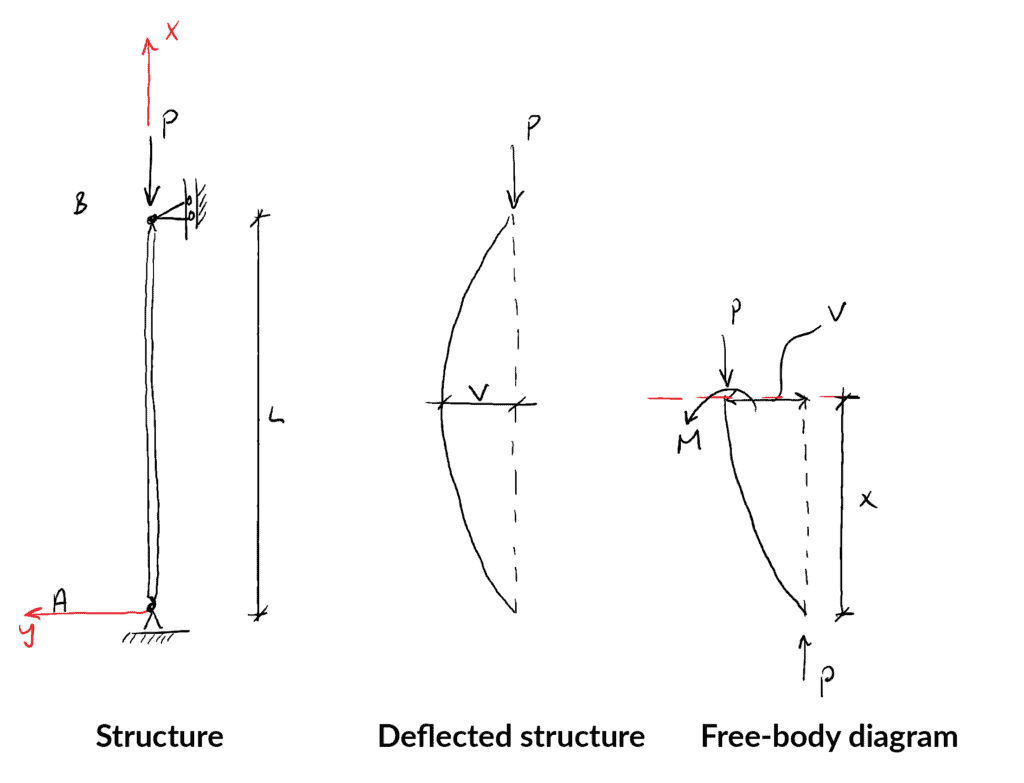
La prise de moments autour du point A donne :

$\begin{align*}M=-Pv\end{align*}$

Substituer à l’équation différentielle de la courbe de déviation et réarranger légèrement donne :

$\begin{align*}\frac{\mathrm{d}^2v}{\mathrm{d}x^2} + \frac{P}{EI}v=0\end{align*}$

C’est une équation différentielle linéaire, homogène, d’ordre 2, à coefficients constants. Il se trouve que c’est aussi une équation qui modélise la forme déviée de notre structure et qui contient , la charge axiale. En suivant la même approche que pour la structure idéalisée abordée précédemment, si nous résolvons cette équation, nous pouvons déterminer $P_{cr}$ , la valeur de la charge appliquée à laquelle elle est équilibrée par la résistance à la flexion de la colonne.

Nous sommes donc confrontés à la résolution d’une équation différentielle. À ce stade, il est utile de pouvoir indiquer la solution générale de cette forme d’équation différentielle :

$\begin{align*}v(x) = C_1 \sin\left(\sqrt{\frac{P}{EI}}x\right) + C_2\cos\left(\sqrt{\frac{P}{EI}}x\right)\end{align*}$

Résolution de l’équation différentielle

Si vous voulez faire un détour à ce stade pour voir comment l’équation différentielle est résolue, regardez la vidéo ci-dessous. Sinon, nous continuerons à travailler sur les constantes d’intégration dans la prochaine section.

Résolution des constantes d’intégration

Maintenant que nous avons la solution générale pour ce format d’équation, nous devons résoudre les constantes d’intégration en utilisant les conditions aux limites (épinglé-épinglé) pour notre colonne.

Condition limite 1:

Au (base de la colonne à l’appui de l’axe), (la déviation latérale doit être égale à zéro. En imposant ces conditions à notre solution générale, on obtient :

$\begin{align*}0=C_1\sin(0) + C_2\cos(0)\end{align*}$

Par conséquent

$\begin{align*}C_2=0\end{align*}$

En conséquence, notre solution se réduit à :

$\begin{align*}v(x)=C_1\sin \left(\sqrt{\frac{P}{EI}}x\right)\end{align*}$

Condition limite 2 :

Au (sommet de la colonne au niveau de l’appui de l’axe), (la déviation latérale est également nulle). De nouveau, en imposant ces conditions aux limites, on obtient,

$\begin{align*}0=C_1\sin\left(\sqrt{\frac{P}{EI}}L\right)\end{align*}$

Donc, soit est égal à zéro, soit $\sin(....)$ est égal à zéro. Si est égal à zéro, l’équation est satisfaite pour toute valeur de . Cela ne nous fait pas vraiment avancer… on peut considérer cette solution comme la solution triviale. Plus intéressant est le cas où :

$\begin{align*}\sin\left(\sqrt{\frac{P}{EI}}L\right)=0\end{align*}$

Sachant ce que nous savons sur les fonctions $\sin$ , cette équation ne peut être vraie que lorsque,

$\begin{align*}\sqrt{\frac{P}{EI}}L = 0, \pi, 2\pi,.....n\pi\end{align*}$

On peut écarter le cas où,

$\begin{align*}\sqrt{\frac{P}{EI}}L = 0\end{align*}$

Dans ce scénario, devrait être égal à zéro (puisque tous les autres termes ont des valeurs non nulles par définition) et nous savons que ce n’est pas le cas. Donc, pour une colonne épinglée, notre solution est la suivante :

$\begin{align*}\sqrt{\frac{P}{EI}}L = n\pi\end{align*}$

où … Enfin, nous pouvons réarranger cette équation pour faire de le sujet de l’équation :

$\begin{align*}P=\frac{n^2\pi^2EI}{L^2}\end{align*}$

Pour …

📌 Cette équation représente une série infinie de charges de flambement. La plus faible est la charge de flambement critique, également appelée charge de flambement d’Euler .

$\begin{align*}P_E = \frac{\pi^2EI}{L^2}\end{align*}$

2.0 Modes de flambement et formes de mode

Jusqu’ici, nous avons établi qu’il existe une série infinie de charges de flambement et que la plus basse est la critique et appelée charge de flambement d’Euler. Cela soulève la question de savoir à quoi correspondent les charges de flambage plus importantes ?

Ce sont des charges qui correspondent à des modes de flambage plus élevés. À chaque mode de flambement correspond une forme de flambement. Pour approfondir cette question, reportez-vous à notre solution générale après avoir établi que :

$\begin{align*}v(x)=C_1\sin \left(\sqrt{\frac{P}{EI}}x\right)\end{align*}$

L’application de notre deuxième condition aux limites nous a permis d’établir la relation :

$\begin{align*}\sqrt{\frac{P}{EI}}L = n\pi\end{align*}$

La combinaison de ces deux équations donne :

$\begin{align*}v(x)=C_1\sin\left(\frac{n\pi x}{L} \right)\end{align*}$

pour … Cette équation décrit la forme déviée de la colonne pour chaque valeur de la charge de flambement définie ci-dessus. Ce n’est que lorsque la charge axiale a l’une des valeurs données par l’équation (définie précédemment)…

$\begin{align*}P=\frac{n^2\pi^2EI}{L^2}\end{align*}$

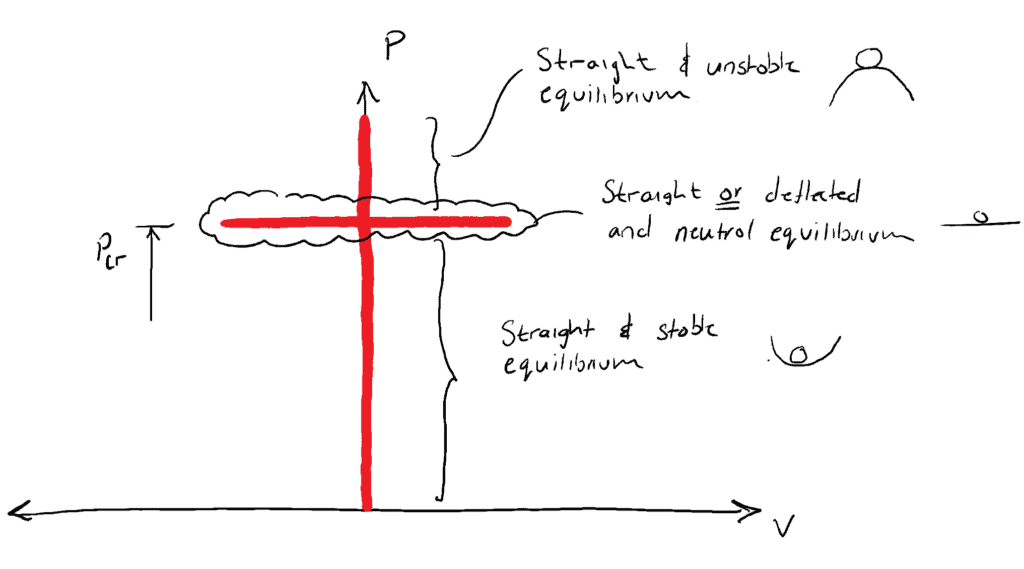
…la colonne peut avoir une forme pliée et être en équilibre. Pour toute autre charge, la colonne serait droite et dans un état d’équilibre STABLE $(PP_{cr})$ ou d’équilibre INSTABLE $(PP_{cr})$ . Nous rappelons ce concept lors de notre précédente discussion ou structures de colonnes idéalisées dans le dernier post :

Flexion maximale sous une charge critique

Notre équation pour la forme déviée ou flambée d’une colonne contient le paramètre , laissé de côté par notre solution générale de l’équation différentielle. Nous reconnaissons maintenant que représente la magnitude de l’onde sinusoïdale ou, dans ce contexte, la déviation latérale maximale pour la déviation/flexion (définie ci-dessus) :

$\begin{align*}v(x)=C_1\sin\left(\frac{n\pi x}{L} \right)\end{align*}$

Si nous rappelons maintenant les états d’équilibre, lorsque la colonne est dans sa forme bouclée $(P=P_{cr})$ et dans un état d’équilibre neutre, la déviation latérale maximale peut avoir n’importe quelle valeur qui satisfait toujours notre hypothèse de petite déviation. Nous pouvons représenter la valeur de graphiquement…

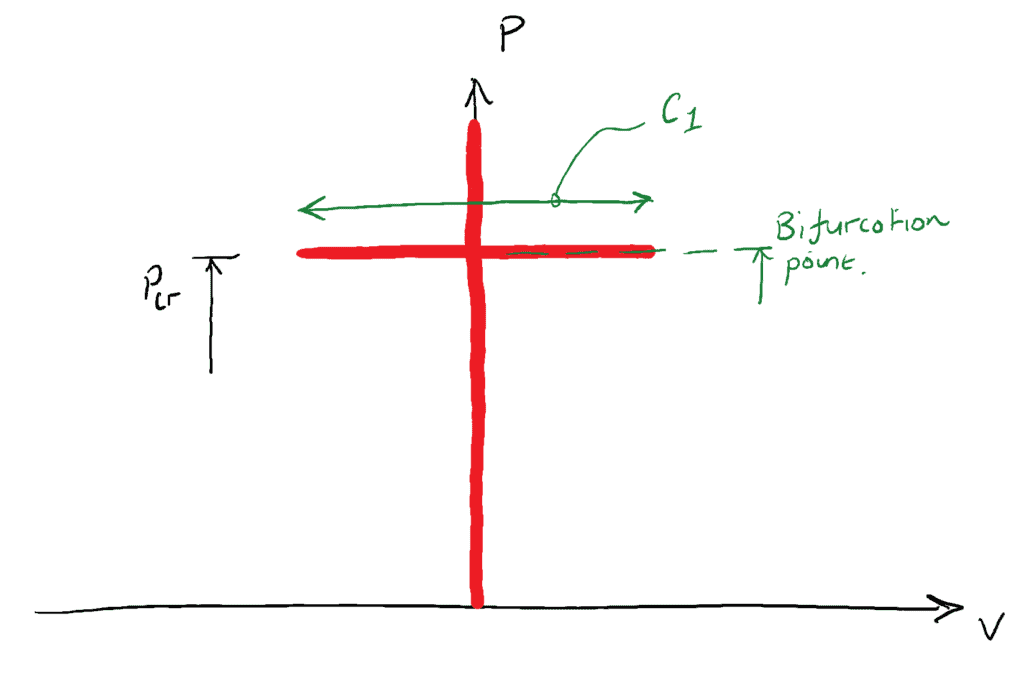
La valeur de est donc mathématiquement indéfinie, elle peut avoir n’importe quelle » petite » valeur. Heureusement, cela ne nous pose aucune difficulté pratique, car comme mentionné précédemment, l’état d’équilibre neutre n’est pas quelque chose que nous observons dans la pratique du génie civil. À toutes fins utiles, pour un ingénieur civil ou structurel, une colonne qui connaît $P_{cr}$ est considérée comme ayant cédé. Cet état théorique d’équilibre neutre est également connu sous le nom de point de bifurcation.

Modes de flambement d’ordre supérieur

Imaginez une colonne d’extrémité goupillée chargée axialement qui est retenue latéralement à son point de mi-hauteur (par une dalle de plancher disons). La colonne serait empêchée de flamber sous la première charge critique (flambement d’Euler) en raison de la retenue latérale. La retenue par la dalle de plancher retient littéralement la colonne et l’empêche de flamber.

En raison de cette retenue, la colonne peut supporter plus de charge, jusqu’à ce qu’elle atteigne la deuxième charge de flambement . Comme la colonne n’est pas retenue contre le flambement dans le deuxième mode, elle se flamberait maintenant (ou entrerait théoriquement dans un état d’équilibre neutre).

💡Une retenue latérale adéquate augmente la résistance d’une colonne au flambement en « fermant » la possibilité de flambement dans les modes inférieurs et en « débloquant » des charges de flambement plus élevées.

Nous pouvons facilement visualiser les trois premiers modes de flambement en évaluant simplement les équations de charge et de forme déviée pour .

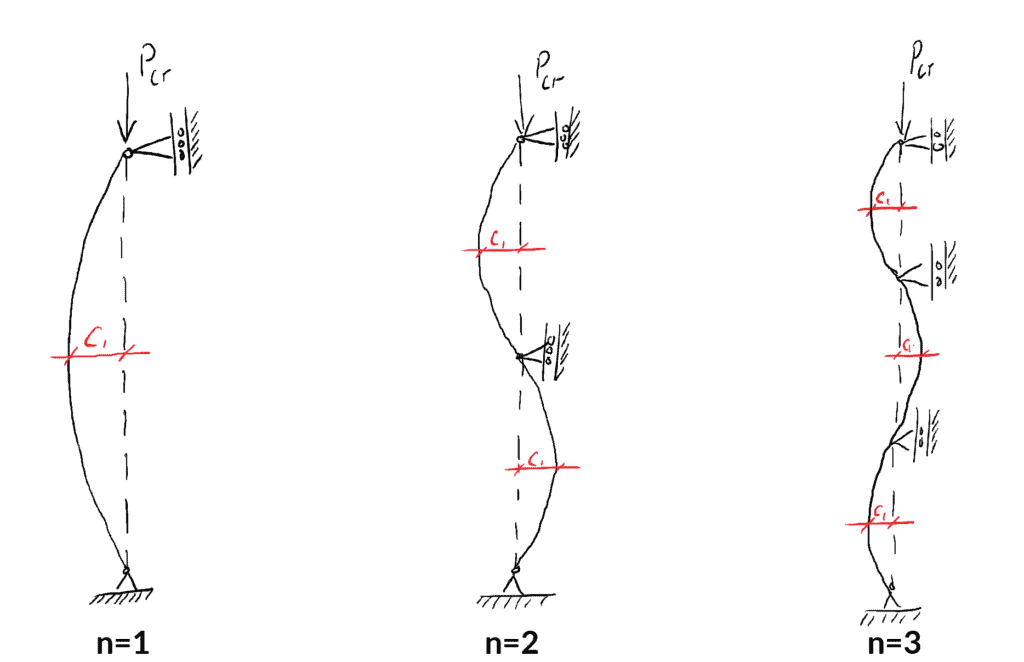
Mode

$\begin{align*}n=1\end{align*}$

$\begin{align*}n=2\end{align*}$

$\begin{align*}n=3\end{align*}$

Charge critique

$\begin{align*}P_{cr} = \frac{{\pi^2EI}{L^2}\end{align*}$

$\begin{align*}P_{cr} = \frac{4\pi^2EI}{L^2}\end{align*}$

$\begin{align*}P_{cr} = \frac{9\pi^2EI}{L^2}\end{align*}$

Forme bouclée

$\begin{align*}v(x) = C_1\sin\left(\frac{\pi x}{L}\right)\end{align*}$

$\begin{align*}v(x) = C_1\sin\left(\frac{2\pi x}{L}\right)\end{align*}$

$\begin{align*}v(x) = C_1\sin\left(\frac{3\pi x}{L}\right)\end{align*}$

📌 Pour tout mode donné, $P_{cr}$ représente la limite supérieure pratique de la charge axiale. Les imperfections naturelles, par exemple une colonne » hors d’aplomb » ou un mauvais alignement de la charge, induiront presque certainement un flambage lorsque la charge critique sera dépassée.

3.0 Colonnes avec d’autres conditions de support

Jusqu’à présent, nous avons examiné le comportement d’une colonne clouée aux deux extrémités. Il s’agit du point de départ typique. Mais le même processus peut être suivi pour déterminer les équations correspondantes pour les colonnes avec différents types de conditions d’appui. Dans les vidéos ci-dessous, je vais effectuer les dérivations pour démontrer le processus pour :

Colonnes dont la base est fixée contre la rotation et libre au sommet (fixe-libre)
Colonnes fixées contre la rotation aux deux extrémités (fixe-fixe)
Colonnes fixées contre la rotation à la base et épinglées au sommet (fixe-…goupillé)

Équation de flambage pour les colonnes retenues contre la rotation aux deux extrémités (fixe-fixe)

Équation de flambage pour les colonnes retenues contre la rotation à la base et libres au sommet (fixe-libre)

Équation de flambement pour les colonnes retenues contre la rotation en bas et épinglées en haut (fixe-goupillés)

Résumé des conditions de support

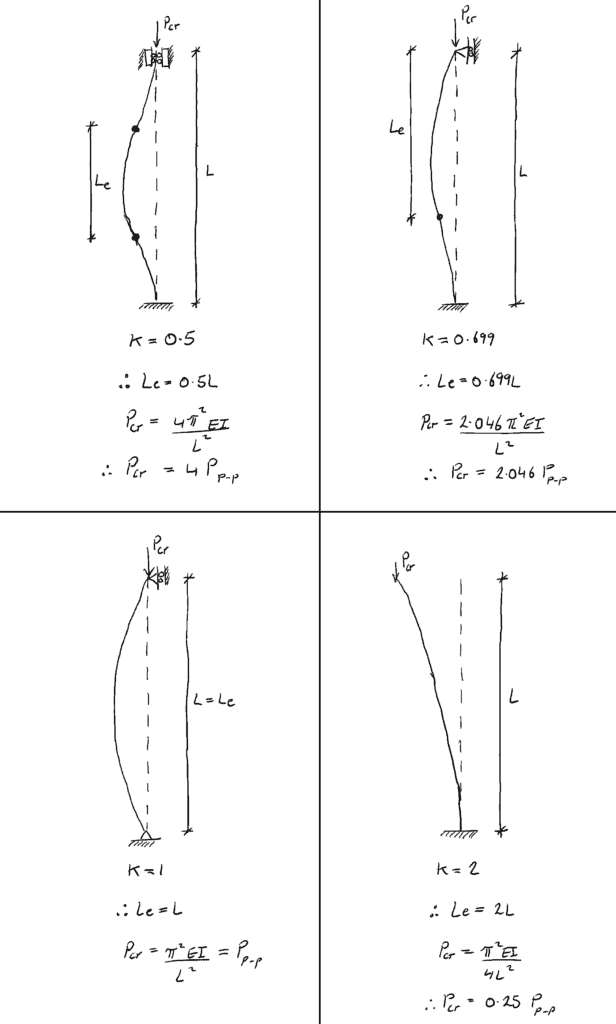
4.0 Axe de flambement

On se souvient de l’équation de la charge de flambement qui est fonction de I, le second moment de l’aire de la section :

$\begin{align*}P=\frac{n^2\pi^2EI}{L^2}\end{align*}$

Donc, pour une section donnée, une colonne se déformera toujours autour de l’axe ayant le second moment d’aire le plus faible, l’axe » le plus faible « . Cela suppose que les deux axes ont une contrainte égale. Considérons le cas d’une section de colonne universelle (UC) soumise à une compression :

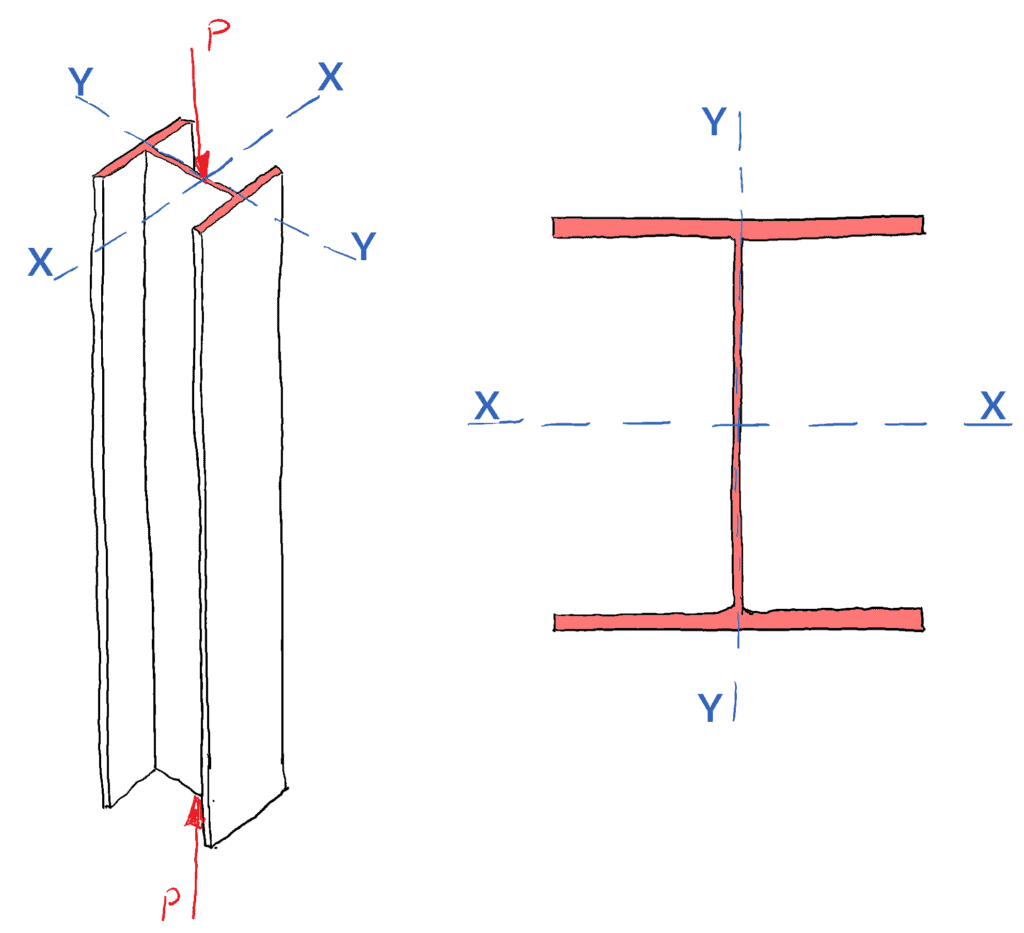
Puisque l’axe X-X, est l’axe de principe majeur (avec la plus grande valeur du second moment d’aire – vous vous en souvenez peut-être de votre étude du cercle de Mohr), c’est l’axe le plus fort et donc la colonne se déformera d’abord autour de l’axe de principe mineur ou axe Y-Y.

Lorsque vous considérez la charge de flambement pour une structure de colonne, la forme de la section transversale joue un rôle clé, vous devez évaluer les axes principaux majeurs et mineurs pour déterminer l’axe critique de flambement.

5.0 Contrainte critique

📌 La contrainte critique est la contrainte axiale moyenne dans une section transversale sous la charge critique

.section sous la charge critique

$\begin{align*}\sigma_{cr}=\frac{P_{cr}}{A}=\frac{\pi^2EI}{AL^2}\end{align*}$

Nous définissons maintenant le rayon de giration, comme :

$\begin{align*}r=\sqrt{\frac{I}{A}}\end{align*}$

Nous pouvons donc écrire la contrainte critique comme :

$\begin{align*}\sigma_{cr}=\frac{\pi^2E}{\left(\frac{L}{r}\right)^2}\end{align*}$

Enfin, nous définissons le rapport d’élancement comme :

$\begin{align*}\lambda=\frac{L}{r}\end{align*}$

Le rapport d’élancement est une mesure très utile de la géométrie d’une colonne et de sa susceptibilité au flambage. Un rapport d’élancement élevé indique une plus grande susceptibilité au flambement. Le coefficient d’élancement doit être déterminé séparément pour chaque axe principal. On peut avoir une intuition du rapport d’élancement en visualisant les deux extrêmes,

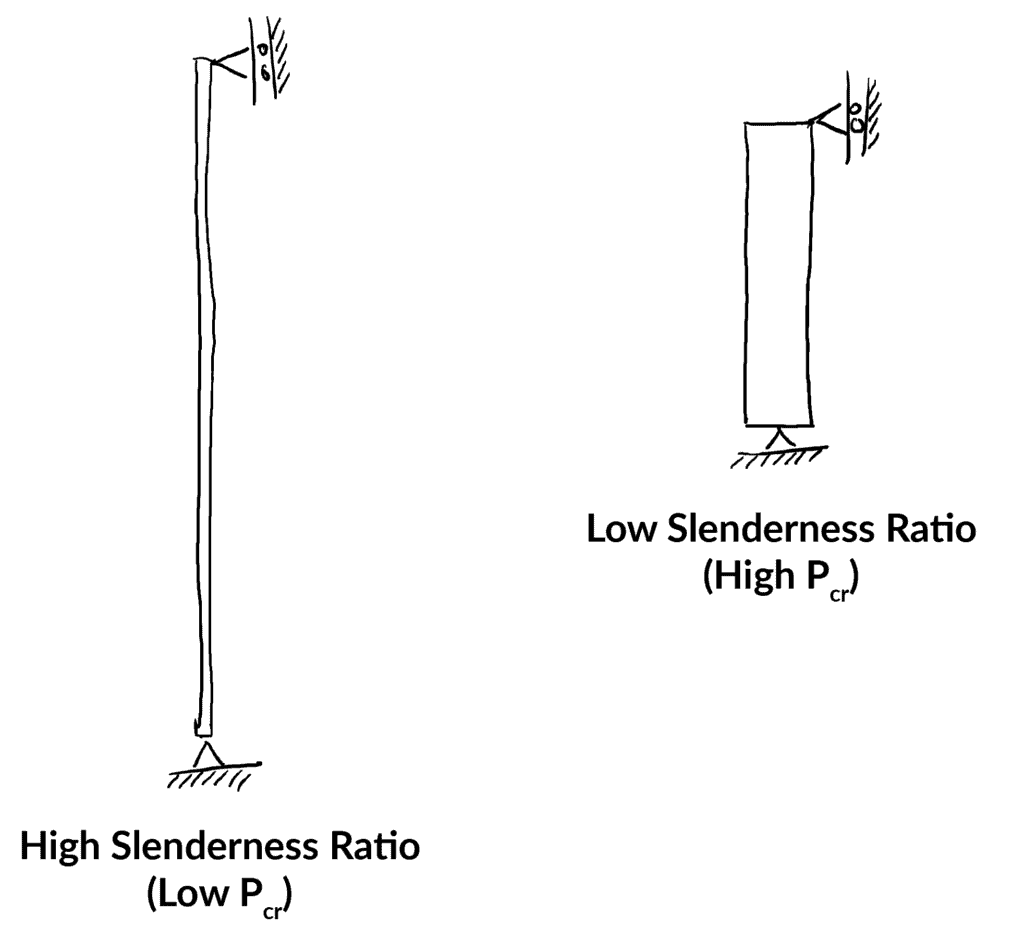
L’équation de la contrainte critique peut donc s’écrire en fonction du rapport d’élancement comme suit ,

$\begin{align*}\sigma_{cr}=\frac{\pi^2E}{\lambda^2}\end{align*}$

Tracer la contrainte critique en fonction du rapport d’élancement pour une valeur valeur du module d’Young donne une courbe d’Euler montrant la plage sûre de la contrainte axiale moyenne pour un rapport d’élancement donné (ou la plage sûre des valeurs du rapport d’élancement pour une contrainte axiale donnée),

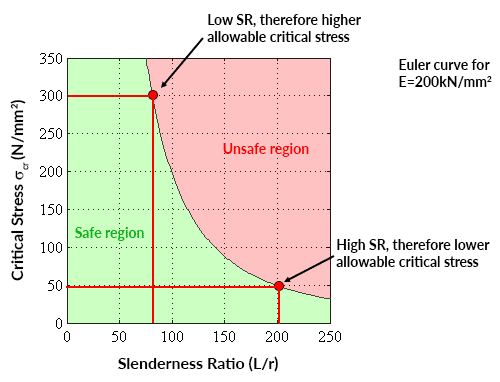
📌 Une courbe d’Euler n’est valable que pour des contraintes critiques inférieures à la limite élastique du matériau

6.0 Longueur effective des colonnes

Le dernier concept que nous allons examiner dans ce post est la longueur effective des colonnes. La longueur effective d’une colonne, , est la longueur entre les points d’inflexion sur la courbe/forme déviée (même si la forme doit être étendue jusqu’à ce qu’un point d’inflexion soit atteint – discuté ci-dessous). Pour une colonne goupillée aux deux extrémités, la longueur effective est simplement la longueur totale de la colonne entre les retenues des goupilles :

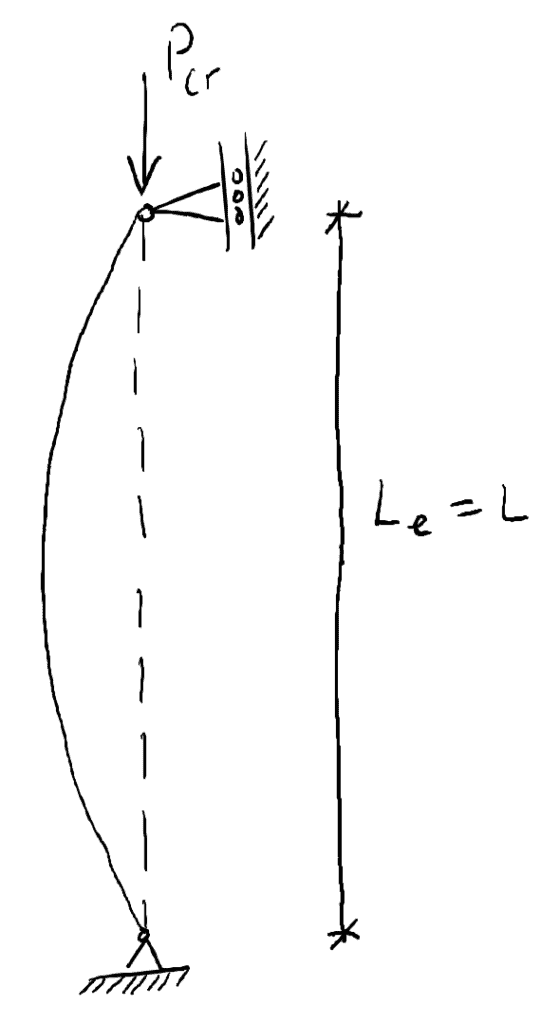
Considérons une colonne avec un support fixe à sa base et aucune retenue latérale au sommet (fixe-libre). À la base, aucune rotation ne peut se produire. Afin d’obtenir deux points d’inflexion sur la forme déviée, il faut l’allonger…

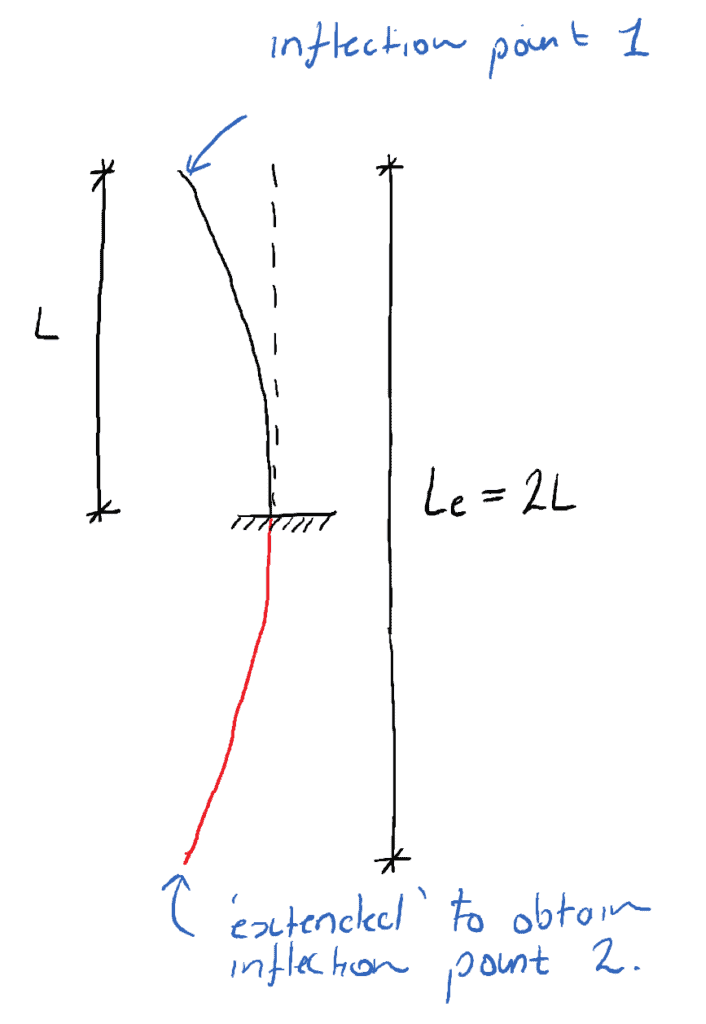
La partie rouge » imaginaire » de la forme déviée est l’extension nécessaire pour fournir le point d’inflexion numéro 2. Ainsi, la longueur effective pour une colonne libre fixée est 2L.

📌 Une autre façon de penser à la longueur effective est qu’il s’agit de la longueur d’une colonne équivalente à extrémité goupillée.

Avant de conclure notre discussion sur la longueur effective, nous pouvons définir une expression générale pour la charge critique comme :

$\begin{align*}P_{cr}=\frac{\pi^2EI}{{L_e}^2}\end{align*}$

Si nous introduisons maintenant le facteur de longueur effective, , tel que , nous pouvons énoncer la charge critique en fonction du facteur de longueur effectif :

$\begin{align*}P_{cr}=\frac{\pi^2EI}{{(KL)}^2}\end{align*}$

S’abonner aux mises à jour

Recevoir une notification lorsque de nouveaux tutoriels et cours atterrissent

1.0 Equation de flambement pour des colonnes goupillées aux deux extrémités

Établissement de l’équation différentielle

Résolution de l’équation différentielle

Résolution des constantes d’intégration

2.0 Modes de flambement et formes de mode

Flexion maximale sous une charge critique

Modes de flambement d’ordre supérieur

3.0 Colonnes avec d’autres conditions de support

Équation de flambage pour les colonnes retenues contre la rotation aux deux extrémités (fixe-fixe)

Équation de flambage pour les colonnes retenues contre la rotation à la base et libres au sommet (fixe-libre)

Équation de flambement pour les colonnes retenues contre la rotation en bas et épinglées en haut (fixe-goupillés)

Résumé des conditions de support

4.0 Axe de flambement

5.0 Contrainte critique

6.0 Longueur effective des colonnes

S’abonner aux mises à jour

Laisser un commentaire Annuler la réponse