Étirement horizontal -Propriétés, graphique et exemples

Vous avez peut-être déjà rencontré des graphiques qui se ressemblent mais partagent des largeurs différentes. Ces fonctions peuvent avoir été étirées horizontalement à l’aide d’une fonction de base. Les étirements horizontaux font partie des techniques de transformation les plus appliquées lors de la représentation graphique des fonctions, il est donc préférable de comprendre sa définition.

Les étirements horizontaux se produisent lorsqu’un graphique de base est élargi le long de l’axe des x et éloigné de l’axe des y.

Apprendre comment nous pouvons étirer les graphiques horizontalement peut nous aider à comprendre la famille des graphiques des fonctions. Nous pouvons également apprendre comment accélérer la représentation graphique de nouvelles fonctions en fonction des facteurs d’échelle appliqués.

Assurez-vous de réviser vos connaissances sur les fonctions parentales, les translations et les étirements verticaux avant de passer à la section suivante.

• Comprendre les fonctions parentales communes que nous pourrions rencontrer.
• Rafraîchir vos connaissances sur les transformations verticales et horizontales.
• Réviser comment nous appliquons les étirements verticaux.

Ces articles liés peuvent vous aider à rafraîchir vos connaissances, et quand vous serez prêt, allons-y et apprenons-en plus sur les étirements horizontaux.

Qu’est-ce qu’un étirement horizontal ?

Nous pouvons appliquer un étirement horizontal à une fonction en multipliant ses valeurs d’entrée par un facteur d’échelle, a, où 0 < 1/a < 1. Qu’est-ce que cela signifie pour des fonctions telles que f(x) ? Lorsque 1/a est multiplié à x, le graphique de f(x) s’étire horizontalement par un facteur d’échelle de a.

Poursuivons et regardons comment f(x) = x2 sera affecté par un facteur d’échelle de 1/2 et 1/3.

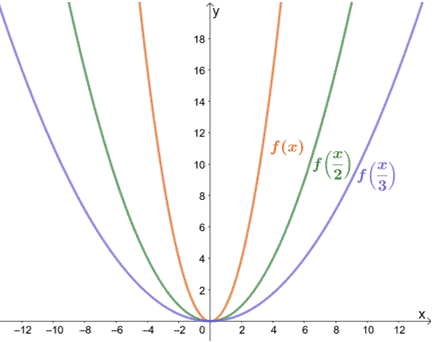
Comme nous l’avons prévu, le graphique s’étire par un facteur de 2 et 3. Vous remarquez que les valeurs des ordonnées restent les mêmes ? C’est vrai pour tous les étirements horizontaux. Le graphique s’étire uniquement en s’éloignant de l’axe des y lorsque nous étirons horizontalement un graphique.

L’étirement horizontal sur d’autres fonctions présentera des propriétés similaires. Disons que nous avons f(x) = |x|, si le graphique de cette fonction doit être étiré horizontalement pour atteindre g(x), l’expression de la nouvelle fonction peut être exprimée sous la forme |1/3 ∙ x| = |x/3|.

Pourquoi ne pas comparer certaines valeurs des deux fonctions ?

.

x	-2	-1	0	1	2
f(x) = |x|	2	1	0	1	1	2

Nous attendons également que toutes ses coordonnées x-augmentent de 3. Lorsque nous faisons cela, les valeurs de sortie resteront les mêmes.

x	-6	-3	0	3	6
g(x) = |x/3|	2	1	0	1	2

Que cela signifie-t-il pour les coordonnées du graphique de la nouvelle fonction ? Si la fonction f(x) passe par (m, n) et est étirée horizontalement par un facteur de 1/a, la nouvelle fonction passera par (am, n).

Comment étirer horizontalement une fonction?

Maintenant que nous avons appris les étirements horizontaux et comment ils affectent une fonction de base, il est temps que nous les appliquions sur les graphiques des fonctions. Avant de commencer à étirer les fonctions horizontalement par un certain facteur, rappelez-vous ces indications pour étirer les graphiques plus rapidement à l’horizontale :

• Ne faites qu’étirer la base du graphique horizontalement pour que les coordonnées y restent dans la même position.
• Puisque les coordonnées y resteront les mêmes, l’ordonnée à l’origine reste la même également.
• Veillez à revérifier les points critiques du graphique, tels que ses ordonnées, ses points maximums, et plus encore.
• Vérifiez si les points de coordonnées sont correctement mis à l’échelle également.

Utilisons le tableau de valeurs présenté dans la section précédente pour tracer les graphiques y = |x| et y = |x/3| afin de visualiser les effets d’un étirement horizontal sur un graphique.

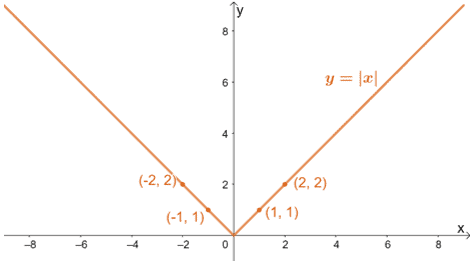
Comme nous en avons discuté, nous nous attendons à ce que les graphiques s’étirent le long de la base, les valeurs de y restant constantes.

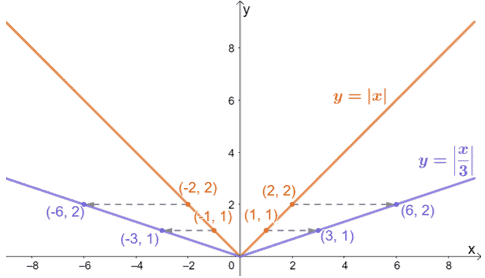
Pour atteindre y = |x/3|, nous étirons la fonction mère y = |x| d’un facteur 3. Le graphique présenté ci-dessus le confirme, et nous pouvons appliquer le même processus lors de l’étirement horizontal des graphiques d’autres fonctions.

Prêts à tracer le graphique d’autres fonctions et à appliquer des étirements horizontaux ? Résumons d’abord ce que nous avons appris jusqu’à présent avant de tenter d’autres questions.

Résumé de la définition et des propriétés de l’étirement horizontal

Voici quelques indications importantes à retenir lorsque vous répondez à des problèmes et que vous tracez des graphiques de fonctions qui impliquent des étirements horizontaux :

• Nous ne pouvons étirer horizontalement un graphique par un facteur de 1/a que lorsque la valeur d’entrée est également augmentée de a.
• Lorsque f(x) est étirée horizontalement en f(ax), multipliez les coordonnées x par a.
• Retenez la position des ordonnées.
• La fonction résultante aura la même étendue mais pourra avoir un domaine différent.
• Donné un point (m, n), il devient (am, n) lorsqu’il est étiré horizontalement.

Retournons toujours à ces cinq points en cas de doute. Être capable de maîtriser la technique de l’étirement horizontal des graphiques peut nous aider à représenter des fonctions plus rapidement et à comprendre leur comportement.

Êtes-vous prêt à tester vos connaissances ? Allons-y et essayons quelques-uns de ces problèmes !

Exemple 1

La fonction, g(x), est obtenue en étirant horizontalement f(x) = 8x par un facteur d’échelle de 1/4. Laquelle des expressions suivantes est la bonne pour g(x) ?

a. g(x) = 32x
b. g(x) =16x
c. g(x) = 2x
d. g(x) =1/2 x

Solution

Souvenez-vous que lorsque nous étirons horizontalement une fonction par 1/a, nous divisons la valeur d’entrée par a. Pourquoi ne pas appliquer cela au problème ? On remplace x par x/4 pour trouver l’expression de g(x).

g(x) = 8(x/4)

Simplifier l’expression conduira à g(x) = 2x.

Exemple 2

Écrivez les expressions de g(x) et h(x) en fonction de f(x) étant donné les conditions suivantes :

a. La fonction g(x) est le résultat de l’étirement horizontal de f(x) par un facteur de 1/5.
b. Lorsque nous étirons horizontalement g(x) par un facteur d’échelle de 1/2, nous obtenons h(x).

Solution

Commençons par g(x). Nous pouvons étirer horizontalement f(x) pour obtenir g(x), donc nous divisons la valeur d’entrée de f(x) par 5 pour obtenir l’expression de g(x) : f(x/5).

Maintenant que nous avons g(x), nous pouvons trouver l’expression de h(x). Nous divisons la valeur d’entrée de g(x) par 2. Par conséquent, nous avons :

h(x) = g(x/2)

= f(x/5 -1/2 )

= f(x/10)

Cela signifie qu’en termes de f(x), g(x) = f(x/5) et h(x)= f(x/10).

Exemple 3

La fonction, f(x), passe par le point (6, 4). Si f(x) est étirée horizontalement par un facteur d’échelle de 1/2, quelle serait la nouvelle coordonnée x du point ?

Solution

Lorsqu’on étire un graphique horizontalement, on multiplie la coordonnée x de la fonction de base par le dénominateur du facteur d’échelle donné pour trouver le nouveau point situé selon la même coordonnée y.

Hence, nous avons (6, 4) → (2 ∙ 6, 4). La nouvelle coordonnée x du point sera (12, 4).

Exemple 4

Le tableau des valeurs de f(x) est présenté ci-dessous. Si h(x) est le résultat de l’étirement horizontal de f(x) par un facteur d’échelle de 1/4, construisez son tableau de valeurs et conservez les valeurs de sortie actuelles.

x	-3	-2	-1	0	1	2	3
f(x)	-6	-4	-2	0	2	4	6

Solution

Lorsque la fonction est étirée horizontalement, nous multiplions les valeurs d’entrée (dans ce cas, ce sont les valeurs de x) par le dénominateur du facteur d’échelle donné.

Cela signifie que (-2, -4) sera transformé en (4∙ -2, -4) = (-8, -4). Nous appliquons le même processus pour le reste des valeurs et nous avons le tableau des valeurs de h(x) comme indiqué ci-dessous.

x	-12	-8	-4	0	4	8	12
h(x)	-6	-4	-2	0	2	4	6

Exemple 5

Observez les fonctions présentées ci-dessous. Quelle est la relation entre f(x) et g(x) ?

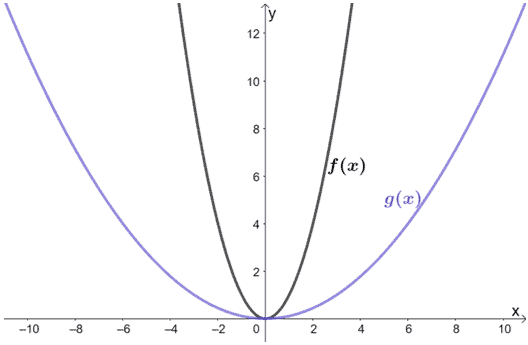
Solution

Juste en regardant le graphique, nous pouvons voir que g(x) résulte de l’étirement horizontal de f(x). Pourquoi ne pas inspecter quelques points des deux graphes ?

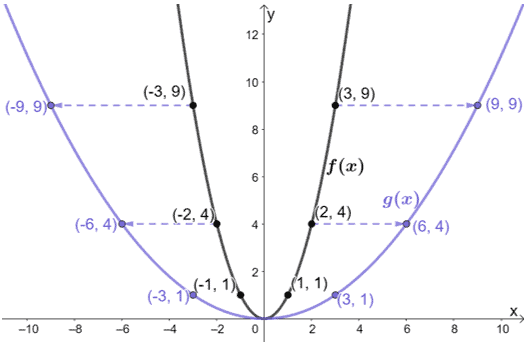
Voici ce qui arrive aux points :

• (-3, 9) → (-9, 9)
• (-2, 4) → (-6, 4)
• (-1, 1) → (-3, 1)
• (0, 0) → (0, 0)
• (1, 1) → (3, 1)
• (2, 4) → (6, 4)
• (3, 9) → (9, 9)

Notez comment pour chaque cas : les coordonnées x de g(x) sont toutes trois fois plus grandes que f(x). Cela signifie que le facteur d’échelle utilisé pour étirer f(x) est 1/3.

La fonction g(x) est le résultat de l’étirement horizontal de f(x) par un facteur d’échelle de 1/3.

Exemple 6

L’image ci-dessous montre le graphique de f(x). Tracez le graphique de g(x) en utilisant le fait qu’il est le résultat de f(x) étiré horizontalement par un facteur de 1/2. Assurez-vous d’inclure les nouveaux points critiques de g(x).

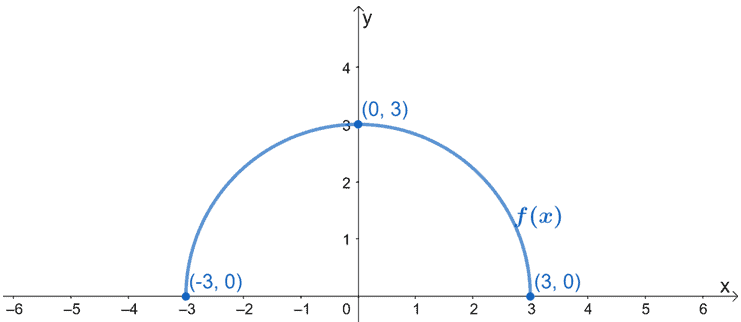
Solution

Parlons d’abord de trouver les nouveaux points critiques de g(x). Puisque f(x) sera étirée horizontalement, nous allons multiplier les coordonnées x par 2. Par conséquent, nous avons les points critiques suivants :

• (-3, 0) → (-6, 0)
• (0, 3) → (0, 3)
• (3, 0) → (6, 0)

Placer ces points et étirer le graphique de f(x) par 3. Assurez-vous que les coordonnées et l’ordonnée à l’origine restent les mêmes.

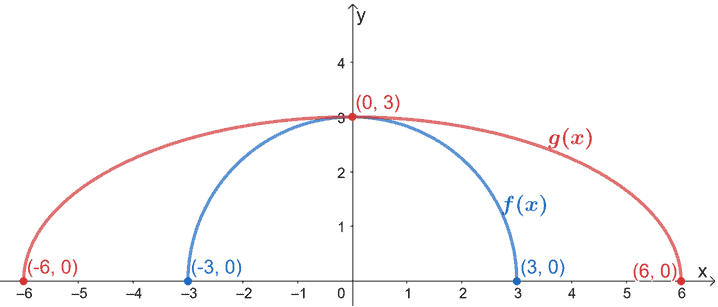
Voici à quoi devrait ressembler le graphique résultant. Puisque g(x) est le résultat de l’étirement horizontal de f(x), nous étirons le graphique de f(x) par une échelle de 3.

Exemple 7

Décrivez les transformations effectuées sur les fonctions suivantes présentées ci-dessous.

a.f(x) = x2 → g(x) = x2/9

b. m(x) = √x → n(x) = 3√(x/4)
c. p(x) = 3x – 1→ q(x) = 3x/4 – 2

Solution

Si vous avez pu remarquer que certaines peuvent ne pas présenter que des étirements horizontaux, vous avez raison !

Ne perdez pas de vue que nous devons parfois appliquer différentes techniques de transformation pour nous permettre d’obtenir l’expression d’une fonction particulière.

Premièrement, commençons par f(x) et g(x) :

Pour vérifier le facteur d’échelle appliqué dans la valeur d’entrée de f(x) pour atteindre g(x), exprimons g(x) comme un carré parfait : g(x) = (x/3)2 = (1/3 – x)2.

Exprimer g(x) en termes de f(x), nous avons g(x) = f(x/3). Par conséquent, g(x) est le résultat de l’étirement horizontal de f(x) par un facteur d’échelle de 1/3.

Passons à m(x) et n(x) :

Nous pouvons voir deux facteurs d’échelle appliqués à n(x) : 3 sur la valeur de sortie et 1/4 pour la valeur d’entrée. En appliquant ce que nous savons sur les étirements verticaux et horizontaux, nous avons n(x) = 3-m(1/4 – x). Ce qui signifie que n(x) est le résultat de m(x) étiré verticalement par un facteur d’échelle de 3 et étiré horizontalement par un facteur d’échelle de 1/4.

Enfin, observons les translations effectuées sur p(x).

q(x) = 3/4 x – 1 – 1

= 3(x/4) – 1 – 1

= p(x/4) – 1

De ce fait, nous pouvons voir que q(x) résulte du fait que p(x) est étiré horizontalement par un facteur d’échelle de 1/4 et traduit d’une unité vers le bas.

Exemple 8

Quelles sont les transformations effectuées sur f(x) pour qu’il en résulte g(x) = 2|x/3| – 1 ? Utilisez le graphique de f(x) présenté ci-dessous pour vous guider. Appliquez les transformations au graphique g(x).

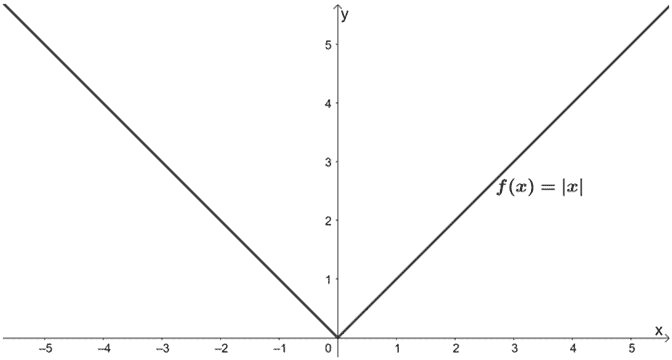
Solution

Allons-y et exprimons g(x) en termes de f(x).

g(x) = 2 – |1/3 – x| – 1

= 2- f(x/3) – 1

Cela signifie que les translations sur f(x) pour obtenir g(x) sont :

• Étirée horizontalement par un facteur d’échelle de 1/3.
• Étiré verticalement par un facteur d’échelle de 2.
• Transformé vers le bas par 1 unité.

Appliquons lentement ces transformations sur f(x), en commençant par étirer horizontalement f(x).

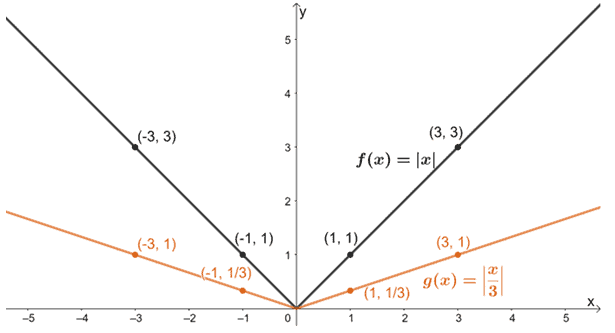
Etendons maintenant le graphique résultant verticalement par un facteur d’échelle de 2.

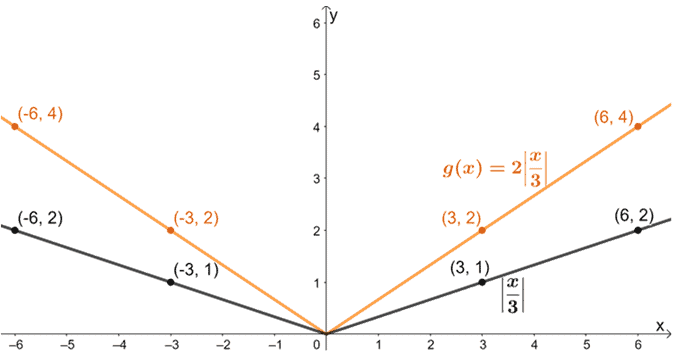
Enfin, translatons le graphique d’une unité vers le bas.

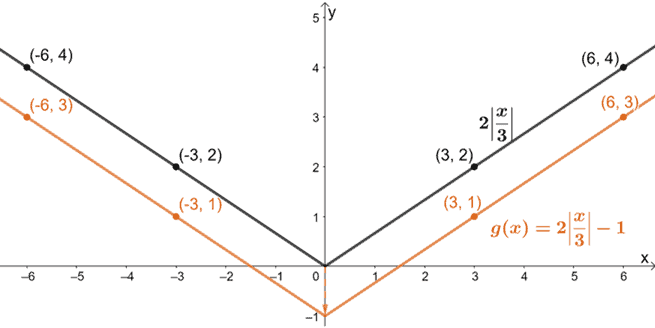
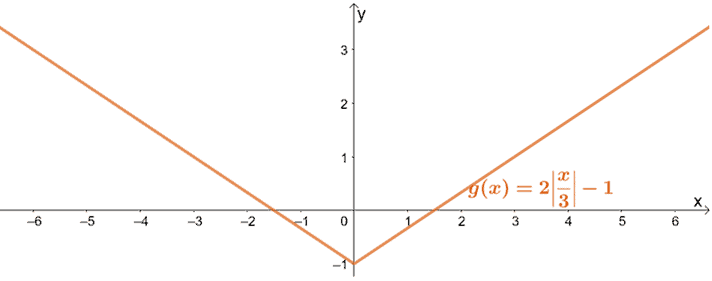
Hence, nous venons de montrer comment g(x) peut être représenté graphiquement à l’aide de la fonction mère des fonctions à valeur absolue, f(x) = |x|.

Questions pratiques

1. La fonction, g(x), est obtenue en étirant horizontalement f(x) = 16×2 par un facteur d’échelle de 2. Laquelle des expressions suivantes est la bonne pour g(x) ?

a. g(x) = 32×2

b. g(x) = 16×2

c. g(x) = 8×2

d. g(x) = 2×2

2. Écrivez les expressions de g(x) et h(x) en termes de f(x) dans les conditions suivantes :

a. La fonction g(x) est le résultat de l’étirement horizontal de f(x) par un facteur 1/4.

b. Lorsqu’on étire horizontalement g(x) par un facteur d’échelle de 1/3, on obtient h(x).

3. La fonction, f(x), passe par le point (10, 8). Si f(x) est étirée horizontalement par un facteur d’échelle de 5, quelle serait la nouvelle coordonnée x du point ?

4. Le tableau des valeurs de f(x) est présenté ci-dessous. Si g(x) est le résultat de l’étirement horizontal de f(x) par un facteur d’échelle de 3, construisez sa table des valeurs et conservez les valeurs de sortie actuelles.

x	-9	-6	-3	0	3	6	9
f(x)	-17	-11	-5	1	7	13	19

5. Observez les fonctions représentées ci-dessous. Quelle est la relation entre f(x) et g(x) ?

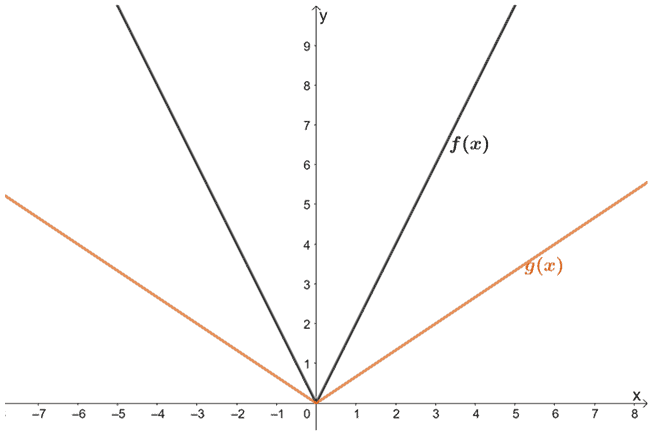
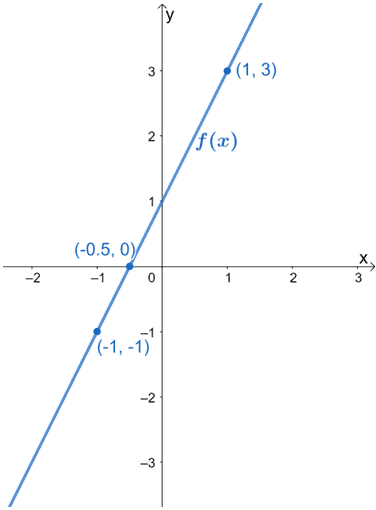
6. L’image ci-dessous montre le graphique de f(x). Tracez le graphique h(x) en utilisant le fait qu’il est le résultat de l’étirement horizontal de f(x) par un facteur 1/3. Assurez-vous d’inclure les nouveaux points critiques de g(x).

7. Décrivez les transformations effectuées sur les fonctions suivantes présentées ci-dessous.

a. f(x) = x2 → g(x) = x2/16

b. m(x) = √x → n(x) = √(x/5) + 3

c. p(x) = 2x + 1→ q(x) = 2x/3 + 2

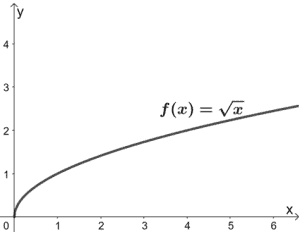
8. Quelles sont les transformations effectuées sur f(x) pour qu’il en résulte g(x) = 3√(x/2) ? Utilisez le graphique de f(x) présenté ci-dessous pour vous guider. Appliquez les transformations au graphique g(x).

Les images/dessins mathématiques sont créés avec GeoGebra.