Hilfreiche SAT-Mathe-Formeln
Eines der ersten Dinge, die man beim Lernen für den SAT-Matheteil tun sollte, ist, sich Formeln einzuprägen. Wenn Sie nicht sicher sind, wo Sie anfangen sollen, wird Ihnen diese Liste helfen.
Hier sind 9 SAT-Mathe-Formeln, die Ihnen bei der Prüfung helfen werden. Nutzen Sie diese Liste als Start.
Lernen Sie noch heute, wie Sie sich mit unseren ganzjährigen SAT-Vorbereitungskursen und ACT-Vorbereitungskursen auf standardisierte Tests vorbereiten können.
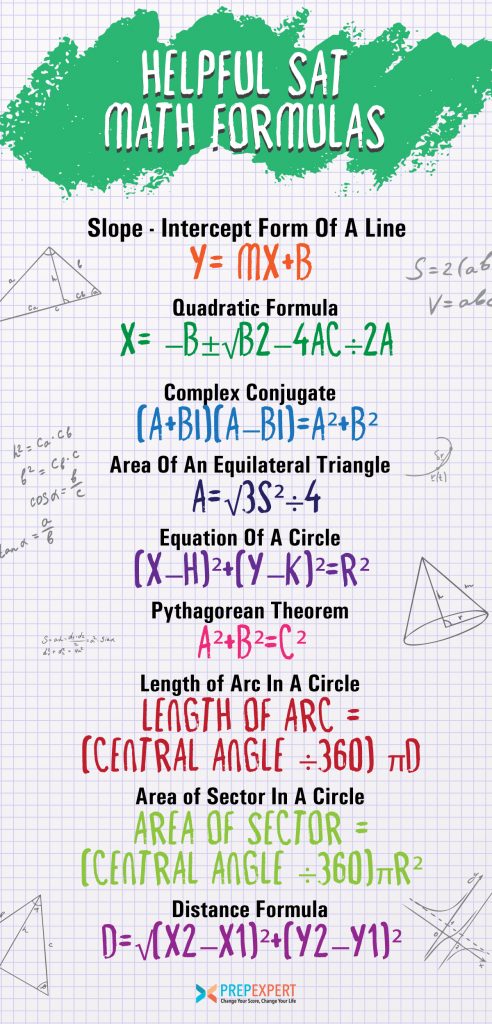
Steilheit-Abschnitt-Form einer Geraden
y=mx+b
„m“ steht für die Steigung der Gleichung, „b“ für den y-Wert des y-Abschnitts. Wenn wir zum Beispiel die Gleichung y=3x+5 haben, dann ist die Steigung „3“ und der y-Achsenabschnitt ist (0,5).
Quadratische Formel
x=-b±√b2-4ac÷2a
Mit dieser Formel kann man die Wurzeln einer quadratischen Gleichung finden, wenn sie nicht einfach faktorisierbar ist. Allerdings muss die Quadratische in der Form y=ax2+bx+c vorliegen.
Zu diesem Zeitpunkt setzen Sie die Koeffizienten und Konstanten in die Formel ein. Denken Sie daran, dass Sie wegen des ± im Zähler zwei separate Antworten erhalten.
Komplex konjugiert
(a+bi)(a-bi)=a²+b²
Die meisten SAT-Mathe-Tests haben mindestens eine Frage, die den Umgang mit imaginären Zahlen erfordert. Mit der komplex-konjugierten Formel können Sie den Imaginärteil einer komplexen Zahl auslöschen. Als Ergebnis erhalten Sie eine reelle Zahl.
Fläche eines gleichseitigen Dreiecks
A=√3s²÷4
Die Formel für die Fläche eines regelmäßigen Dreiecks wird normalerweise auf dem Referenzblatt des Tests angegeben, aber Sie müssen die Höhe des Dreiecks kennen. Manchmal wird die Höhe nicht angegeben und Sie müssen sie selbst herausfinden.
Die gute Nachricht ist, dass Sie den Flächeninhalt eines gleichseitigen Dreiecks berechnen können, indem Sie die Länge einer der Seiten in diese Formel einsetzen. Sie können die Höhenanforderung überspringen!
Gleichung eines Kreises
(x-h)²+(y-k)²=r²
Normalerweise wird in einer SAT-Mathe-Frage die Gleichung eines Kreises verlangt. In dieser Gleichung stellen die Variablen h und k die Koordinaten für den Mittelpunkt des Kreises dar und r
stellt den Radius des Kreises dar.
Pythagoreischer Satz
a²+b²=c²
Der Pythagoreische Satz gilt für regelmäßige rechtwinklige Dreiecke. Sein Zweck ist es, Sie für eine der unbekannten Seitenlängen zu lösen, wenn eine andere Seitenlänge gegeben ist. a und b sind die Schenkel des Dreiecks, und c ist die Hypotenuse.
Bogenlänge in einem Kreis
Bogenlänge = (Zentralwinkel ÷360) πd
Geometrische Fragen sind im SAT-Mathe-Teil nicht häufig, aber Sie werden wahrscheinlich trotzdem eine Frage über Bögen oder Sektoren in einem Kreis gestellt bekommen. Ein Bogen ist eine Länge zwischen zwei Punkten auf einem Kreis.
Sie werden normalerweise gemessen, indem man zwei Radien vom Mittelpunkt des Kreises aus verlängert und einen Winkel zwischen ihnen bildet. Sie können das Gradmaß dieses Bogens als einen Bruchteil von 360 verwenden und dann mit der Gleichung für den Umfang multiplizieren, um die Bogenlänge zu finden.
Fläche des Sektors in einem Kreis
Fläche des Sektors = (Zentralwinkel ÷360)πr²
Im Gegensatz zu einem Bogen ist der Sektor eines Kreises die Fläche zwischen zwei Radien, die sich vom Zentrum aus erstrecken. Stellen Sie sich das im Grunde wie ein Stück Kuchen vor. Auch hier multiplizieren Sie das Gradmaß als Bruchteil von 360 und multiplizieren es dann mit der Gleichung für die Fläche eines Kreises, um die Fläche des Sektors zu finden.
Abstandsformel
d=√(x2-x1)²+(y2-y1)²
Die Abstandsformel ist fantastisch, um den Abstand zwischen zwei Punkten schnell zu bestimmen. Um sie zu verwenden, nehmen Sie einfach die Koordinatenwerte und setzen Sie sie ein, um den Abstand zu finden. Und achten Sie darauf, die Quadrate und die Quadratwurzel im richtigen Schritt anzuwenden.
Für weitere Tipps zu Teststrategien, College-Zulassungen und Stipendienbewerbungen melden Sie sich für unseren KOSTENLOSEN Kurs an, der jetzt stattfindet!