Horizontale Streckung -Eigenschaften, Graph und Beispiele

Sie sind vielleicht schon auf Graphen gestoßen, die gleich aussehen, aber unterschiedliche Breiten haben. Diese Funktionen wurden möglicherweise mit Hilfe einer Basisfunktion horizontal gestreckt. Horizontale Streckungen gehören zu den am häufigsten angewandten Transformationstechniken bei der Darstellung von Funktionen, daher ist es am besten, ihre Definition zu verstehen.

Horizontale Streckungen geschehen, wenn ein Basisgraph entlang der x-Achse und weg von der y-Achse verbreitert wird.

Zu lernen, wie wir Graphen horizontal strecken können, kann uns helfen, die Familie der Graphen von Funktionen zu verstehen. Wir können auch lernen, wie wir die Darstellung neuer Funktionen basierend auf den angewendeten Skalierungsfaktoren beschleunigen können.

Achten Sie darauf, Ihr Wissen über übergeordnete Funktionen, Übersetzungen und vertikale Streckungen zu überprüfen, bevor Sie zum nächsten Abschnitt übergehen.

• Verstehen Sie die häufigen übergeordneten Funktionen, denen wir begegnen könnten.
• Frischen Sie Ihr Wissen über vertikale und horizontale Transformationen auf.
• Überprüfen Sie, wie wir vertikale Streckungen anwenden.

Diese verlinkten Artikel können Ihnen helfen, Ihr Wissen aufzufrischen, und wenn Sie bereit sind, lassen Sie uns fortfahren und mehr über horizontale Streckungen lernen.

Was ist eine horizontale Streckung?

Wir können eine horizontale Streckung auf eine Funktion anwenden, indem wir ihre Eingabewerte mit einem Skalierungsfaktor, a, multiplizieren, wobei 0 < 1/a < 1. Was bedeutet das für Funktionen wie f(x)? Wenn 1/a mit x multipliziert wird, streckt sich der Graph von f(x) horizontal um einen Skalierungsfaktor von a.

Schauen wir uns nun an, wie sich f(x) = x2 bei einem Skalierungsfaktor von 1/2 und 1/3 verhält.

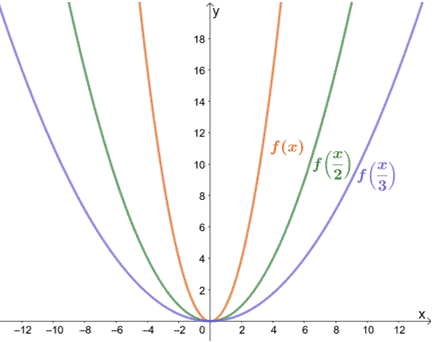
Wie wir erwartet haben, streckt sich der Graph um den Faktor 2 und 3. Beachten Sie, dass die y-Werte gleich bleiben. Dies gilt für alle horizontalen Streckungen. Der Graph streckt sich nur von der y-Achse weg, wenn wir einen Graphen horizontal strecken.

Die horizontale Streckung bei anderen Funktionen wird ähnliche Eigenschaften aufweisen. Nehmen wir an, wir haben f(x) = |x|, wenn der Graph dieser Funktion horizontal gestreckt werden soll, um g(x) zu erhalten, kann der Ausdruck der neuen Funktion als |1/3 ∙ x| = |x/3| ausgedrückt werden.

Warum vergleichen wir nicht einige Werte aus beiden Funktionen?

x	-2	-1	0	1	2
f(x) = |x|	2	1	0	1	2

Wir erwarten auch, dass alle seine x-Koordinaten um 3 zu erhöhen. Wenn wir das tun, bleiben die Ausgangswerte gleich.

x	-6	-3	0	3	6
g(x) = |x/3|	2	1	0	1	2

Was bedeutet das für die Koordinaten des Graphen der neuen Funktion? Wenn die Funktion f(x) durch (m, n) verläuft und horizontal um den Faktor 1/a gedehnt wird, verläuft die neue Funktion durch (am, n).

Wie dehnt man eine Funktion horizontal?

Nachdem wir nun die horizontalen Dehnungen und ihre Auswirkungen auf eine Basisfunktion kennengelernt haben, ist es an der Zeit, diese auf die Graphen der Funktionen anzuwenden. Bevor wir damit beginnen, Funktionen horizontal um einen bestimmten Faktor zu dehnen, sollten Sie sich diese Hinweise merken, um Graphen schneller horizontal zu dehnen:

• Die Basis des Graphen darf nur horizontal gedehnt werden, damit die y-Koordinaten an der gleichen Stelle bleiben.
• Da die y-Koordinaten gleich bleiben, bleibt auch der y-Achsenabschnitt gleich.
• Überprüfen Sie kritische Punkte des Graphen, wie z. B. die Achsenabschnitte, die Maximalpunkte und mehr.
• Sehen Sie nach, ob die Koordinatenpunkte auch richtig skaliert sind.

Lassen Sie uns die Wertetabelle aus dem vorherigen Abschnitt verwenden, um sowohl y = |x| als auch y = |x/3| grafisch darzustellen, um die Auswirkungen einer horizontalen Streckung auf einen Graphen zu visualisieren.

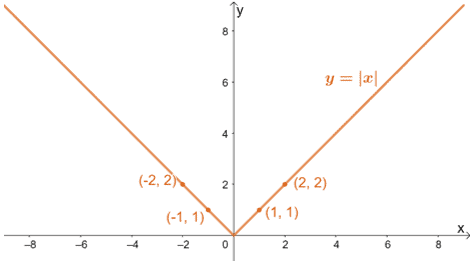
Wie besprochen, erwarten wir, dass sich die Graphen entlang der Basis strecken, wobei die Werte für y konstant bleiben.

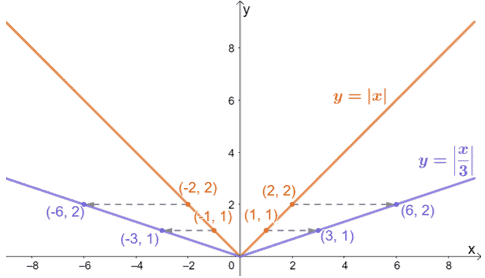
Um y = |x/3| zu erhalten, strecken wir die übergeordnete Funktion y = |x| um den Faktor 3. Der oben gezeigte Graph bestätigt dies, und wir können den gleichen Prozess anwenden, wenn wir die Graphen anderer Funktionen horizontal strecken.

Bereit, weitere Funktionen zu graphen und horizontale Streckungen anzuwenden? Lassen Sie uns zunächst zusammenfassen, was wir bisher gelernt haben, bevor wir weitere Fragen ausprobieren.

Zusammenfassung der Definition und Eigenschaften der horizontalen Streckung

Hier sind einige wichtige Hinweise, die Sie sich merken sollten, wenn Sie Aufgaben lösen und Funktionen grafisch darstellen, die horizontale Streckungen beinhalten:

• Wir können einen Graphen nur dann horizontal um den Faktor 1/a strecken, wenn der Eingabewert ebenfalls um a erhöht wird.
• Wenn f(x) horizontal zu f(ax) gestreckt wird, multiplizieren Sie die x-Koordinaten mit a.
• Behalten Sie die Position der y-Achsenpunkte bei.
• Die resultierende Funktion hat denselben Bereich, kann aber einen anderen haben.
• Gegeben einen Punkt (m, n), wird er zu (am, n), wenn er horizontal gestreckt wird.

Lassen Sie uns im Zweifelsfall immer auf diese fünf Punkte zurückgreifen. Wenn wir die Technik des horizontalen Streckens von Graphen beherrschen, können wir Funktionen schneller grafisch darstellen und ihr Verhalten verstehen.

Sind Sie bereit, Ihr Wissen zu testen? Lassen Sie uns loslegen und einige dieser Probleme ausprobieren!

Beispiel 1

Die Funktion g(x) erhält man durch horizontales Strecken von f(x) = 8x um den Skalenfaktor 1/4. Welcher der folgenden ist der richtige Ausdruck für g(x)?

a. g(x) = 32x
b. g(x) =16x
c. g(x) = 2x
d. g(x) =1/2 x

Lösung

Erinnern Sie sich, dass wir, wenn wir eine Funktion horizontal um 1/a strecken, den Eingabewert durch a teilen. Warum wenden wir das nicht auf das Problem an? Wir ersetzen x durch x/4, um den Ausdruck für g(x) zu finden.

g(x) = 8(x/4)

Vereinfacht man den Ausdruck, erhält man g(x) = 2x.

Beispiel 2

Schreiben Sie die Ausdrücke für g(x) und h(x) in Abhängigkeit von f(x) unter folgenden Bedingungen:

a. Die Funktion g(x) ist das Ergebnis einer horizontalen Streckung von f(x) um den Faktor 1/5.
b. Wenn wir g(x) horizontal um einen Skalierungsfaktor von 1/2 strecken, erhalten wir h(x).

Lösung

Beginnen wir mit g(x). Wir können f(x) horizontal strecken, um g(x) zu erhalten, also teilen wir den Eingangswert von f(x) durch 5, um den Ausdruck von g(x) zu erhalten: f(x/5).

Nun, da wir g(x) haben, können wir den Ausdruck für h(x) finden. Wir teilen den Eingangswert von g(x) durch 2. Daher haben wir:

h(x) = g(x/2)

= f(x/5 -1/2 )

= f(x/10)

Das bedeutet, dass in Bezug auf f(x), g(x) = f(x/5) und h(x)= f(x/10).

Beispiel 3

Die Funktion, f(x), geht durch den Punkt (6, 4). Wenn f(x) horizontal um den Skalierungsfaktor 1/2 gestreckt wird, was wäre dann die neue x-Koordinate des Punktes?

Lösung

Wenn wir einen Graphen horizontal strecken, multiplizieren wir die x-Koordinate der Basisfunktion mit dem Nenner des gegebenen Skalierungsfaktors, um den neuen Punkt zu finden, der auf der gleichen y-Koordinate liegt.

Daher haben wir (6, 4) → (2 ∙ 6, 4). Die neue x-Koordinate des Punktes ist dann (12, 4).

Beispiel 4

Die Wertetabelle für f(x) ist unten dargestellt. Wenn h(x) das Ergebnis einer horizontalen Streckung von f(x) um einen Skalierungsfaktor von 1/4 ist, konstruieren Sie die Wertetabelle und behalten Sie die aktuellen Ausgabewerte bei.

x	-3	-2	-1	0	1	2	3
f(x)	-6	-4	-2	0	2	4	6

Lösung

Wenn die Funktion horizontal gestreckt wird, multiplizieren wir die Eingabewerte (in diesem Fall sind es die Werte von x) mit dem Nenner des angegebenen Skalierungsfaktors.

Das bedeutet, dass (-2, -4) in (4∙ -2, -4) = (-8, -4) transformiert wird. Wir wenden das gleiche Verfahren für die restlichen Werte an und haben die Wertetabelle von h(x) wie unten dargestellt.

x	-12	-8	-4	0	4	8	12
h(x)	-6	-4	-2	0	2	4	6

Beispiel 5

Betrachten Sie die unten dargestellten Funktionen. Welcher Zusammenhang besteht zwischen f(x) und g(x)?

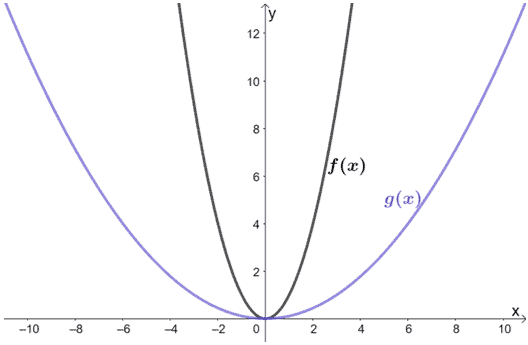
Lösung

Beim Betrachten des Graphen können wir sehen, dass g(x) aus der horizontalen Streckung von f(x) resultiert. Warum untersuchen wir nicht einige Punkte aus beiden Graphen?

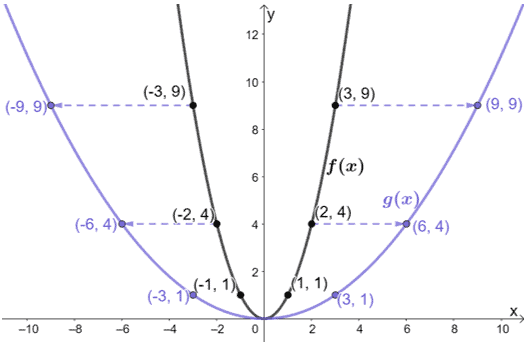
Das ist, was mit den Punkten passiert:

• (-3, 9) → (-9, 9)
• (-2, 4) → (-6, 4)
• (-1, 1) → (-3, 1)
• (0, 0) → (0, 0)
• (1, 1) → (3, 1)
• (2, 4) → (6, 4)
• (3, 9) → (9, 9)

Beachte, wie für jeden Fall: Die x-Koordinaten von g(x) sind alle dreimal so groß wie f(x). Das bedeutet, dass der Skalierungsfaktor, mit dem f(x) gestreckt wurde, 1/3 beträgt.

Die Funktion g(x) ist das Ergebnis der horizontalen Streckung von f(x) um den Skalierungsfaktor 1/3.

Beispiel 6

Das folgende Bild zeigt den Graphen von f(x). Graphen Sie g(x) unter Verwendung der Tatsache, dass es das Ergebnis einer horizontalen Streckung von f(x) um den Faktor 1/2 ist. Achten Sie darauf, die neuen kritischen Punkte für g(x) einzuschließen.

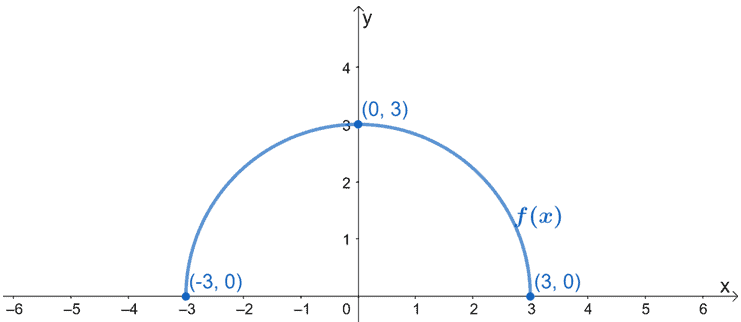
Lösung

Lassen Sie uns zunächst die neuen kritischen Punkte von g(x) finden. Da f(x) horizontal gestreckt wird, multiplizieren wir die x-Koordinaten mit 2. Daraus ergeben sich die folgenden kritischen Punkte:

• (-3, 0) → (-6, 0)
• (0, 3) → (0, 3)
• (3, 0) → (6, 0)

Tragen Sie diese Punkte ein und strecken Sie den Graphen von f(x) um 3. Achten Sie darauf, dass die y-Koordinaten und der y-Achsenabschnitt gleich bleiben.

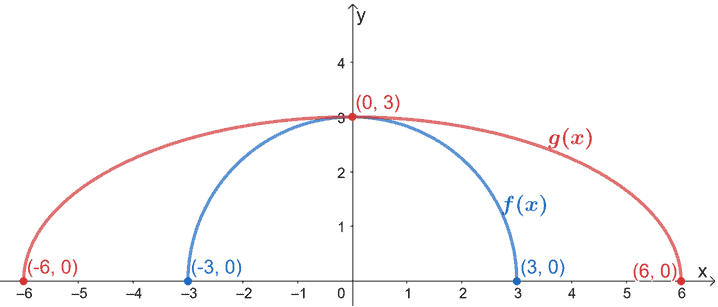
So sollte der resultierende Graph aussehen. Da g(x) das Ergebnis der horizontalen Streckung von f(x) ist, strecken wir den Graphen von f(x) um den Faktor 3.

Beispiel 7

Beschreiben Sie die Transformationen, die an den folgenden Funktionen durchgeführt werden.

a.f(x) = x2 → g(x) = x2/9

b. m(x) = √x → n(x) = 3√(x/4)
c. p(x) = 3x – 1→ q(x) = 3x/4 – 2

Lösung

Wenn Sie bemerkt haben, dass einige nicht nur horizontale Streckungen aufweisen, haben Sie recht!

Denken Sie daran, dass wir manchmal verschiedene Transformationsverfahren anwenden müssen, um den Ausdruck einer bestimmten Funktion zu erhalten.

Beginnen wir mit f(x) und g(x):

Um den Skalierungsfaktor zu überprüfen, der auf den Eingabewert von f(x) angewendet wird, um g(x) zu erhalten, drücken wir g(x) als perfektes Quadrat aus: g(x) = (x/3)2 = (1/3 – x)2.

Wenn wir g(x) in Bezug auf f(x) ausdrücken, haben wir g(x) = f(x/3). Folglich ist g(x) das Ergebnis der horizontalen Streckung von f(x) um den Skalierungsfaktor 1/3.

Weiter zu m(x) und n(x):

Wir sehen zwei Skalierungsfaktoren, die auf n(x) angewendet werden: 3 für den Ausgangswert und 1/4 für den Eingangswert. Wenn wir das anwenden, was wir über vertikale und horizontale Ausdehnungen wissen, haben wir n(x) = 3-m(1/4 – x). Das heißt, n(x) ist das Ergebnis der vertikalen Streckung von m(x) um den Skalierungsfaktor 3 und der horizontalen Streckung um den Skalierungsfaktor 1/4.

Zuletzt betrachten wir noch die Translationen, die an p(x) vorgenommen werden.

q(x) = 3/4 x – 1 – 1

= 3(x/4) – 1 – 1

= p(x/4) – 1

Daraus können wir ersehen, dass q(x) daraus resultiert, dass p(x) horizontal um den Skalierungsfaktor 1/4 gestreckt und um eine Einheit nach unten übersetzt wird.

Beispiel 8

Welche Transformationen werden an f(x) vorgenommen, so dass sich g(x) = 2|x/3| – 1 ergibt? Verwenden Sie den unten gezeigten Graphen von f(x) als Anhaltspunkt. Wenden Sie die Transformationen an, um den Graphen g(x) darzustellen.

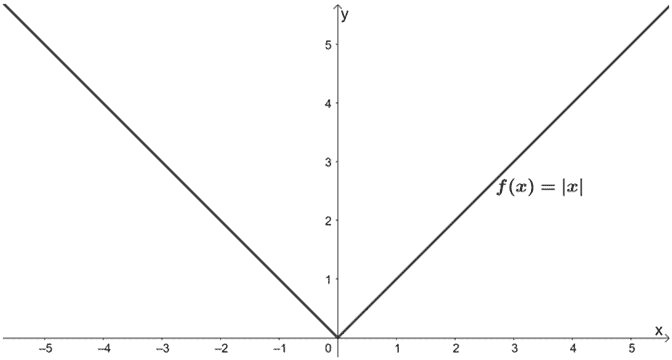
Lösung

Lassen Sie uns fortfahren und g(x) in Termen von f(x) ausdrücken.

g(x) = 2 – |1/3 – x| – 1

= 2- f(x/3) – 1

Das bedeutet, dass die Translationen auf f(x), um g(x) zu erhalten, sind:

• Horizontal gestreckt um einen Skalenfaktor von 1/3.
• Vertikal gestreckt um den Skalenfaktor 2.
• Translatiert nach unten um 1 Einheit.

Lassen Sie uns diese Transformationen langsam auf f(x) anwenden, beginnend mit der horizontalen Streckung von f(x).

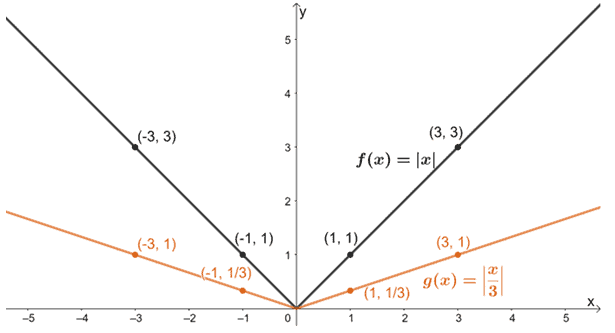
Lassen Sie uns nun den resultierenden Graphen vertikal um einen Skalierungsfaktor von 2 strecken.

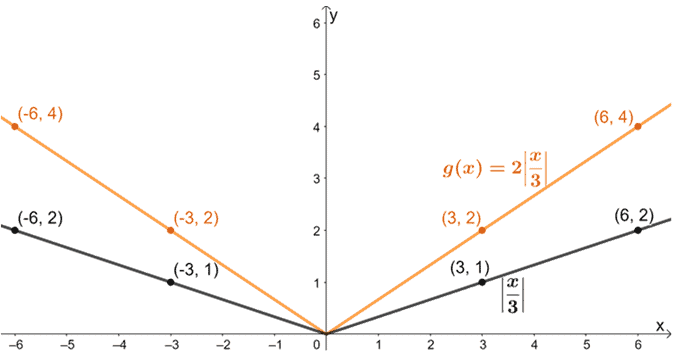
Zuletzt verschieben wir den Graphen noch um eine Einheit nach unten.

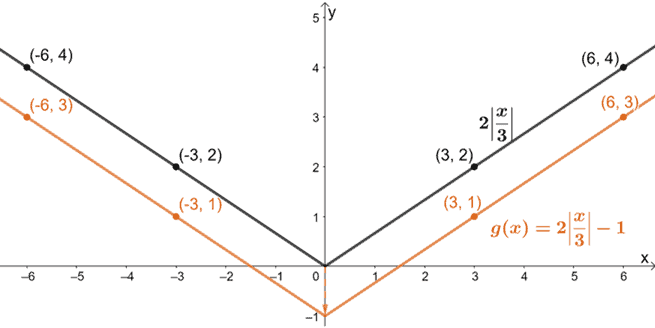
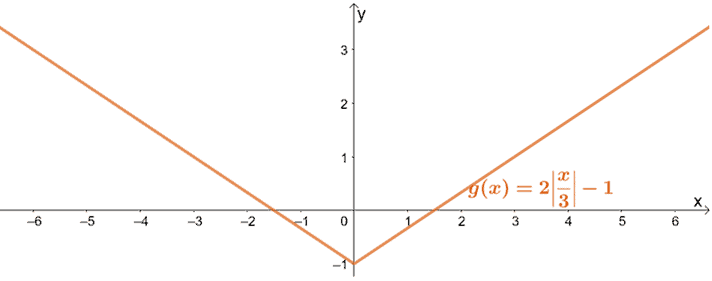
Soeben haben wir gezeigt, wie g(x) mit Hilfe der Stammfunktion der Absolutwertfunktionen, f(x) = |x|, grafisch dargestellt werden kann.

Praxisfragen

1. Die Funktion g(x) erhält man durch horizontale Streckung von f(x) = 16×2 um den Skalenfaktor 2. Welcher der folgenden Ausdrücke ist der richtige für g(x)?

a. g(x) = 32×2

b. g(x) = 16×2

c. g(x) = 8×2

d. g(x) = 2×2

2. Schreiben Sie die Ausdrücke für g(x) und h(x) in Abhängigkeit von f(x) unter folgenden Bedingungen:

a. Die Funktion g(x) ergibt sich aus der horizontalen Streckung von f(x) um den Faktor 1/4.

b. Wenn wir g(x) horizontal um einen Skalierungsfaktor von 1/3 strecken, erhalten wir h(x).

3. Die Funktion f(x) geht durch den Punkt (10, 8). Wenn f(x) horizontal um den Skalierungsfaktor 5 gestreckt wird, was wäre dann die neue x-Koordinate des Punktes?

4. Die Wertetabelle für f(x) ist unten dargestellt. Wenn g(x) das Ergebnis einer horizontalen Streckung von f(x) um den Skalierungsfaktor 3 ist, konstruieren Sie dessen Wertetabelle und behalten Sie die aktuellen Ausgangswerte bei.

x	-9	-6	-3	0	3	6	9
f(x)	-17	-11	-5	1	7	13	19

5. Betrachten Sie die unten dargestellten Funktionen. Welcher Zusammenhang besteht zwischen f(x) und g(x)?

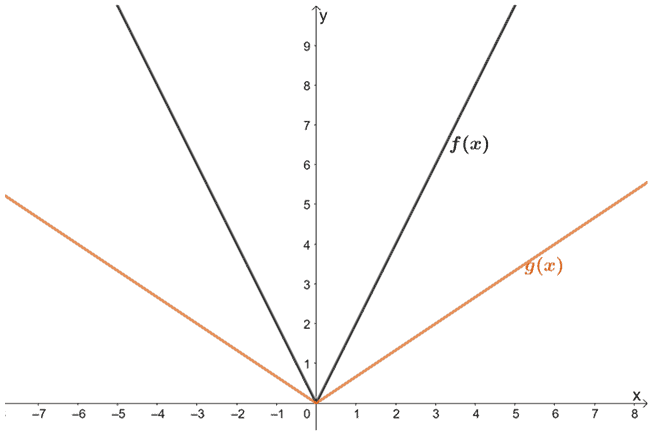
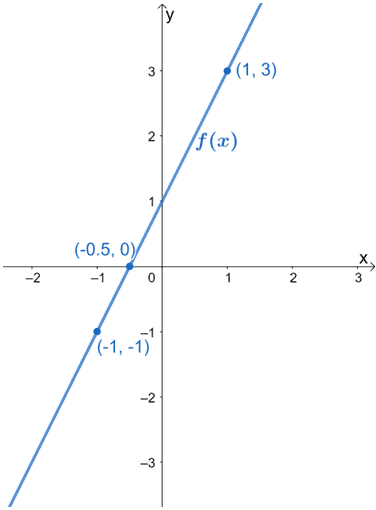
6. Die folgende Abbildung zeigt den Graphen von f(x). Zeichnen Sie den Graphen h(x), indem Sie die Tatsache nutzen, dass er das Ergebnis der horizontalen Streckung von f(x) um den Faktor 1/3 ist. Achten Sie darauf, die neuen kritischen Punkte für g(x) einzubeziehen.

7. Beschreiben Sie die Transformationen, die an den folgenden Funktionen vorgenommen wurden.

a. f(x) = x2 → g(x) = x2/16

b. m(x) = √x → n(x) = √(x/5) + 3

c. p(x) = 2x + 1→ q(x) = 2x/3 + 2

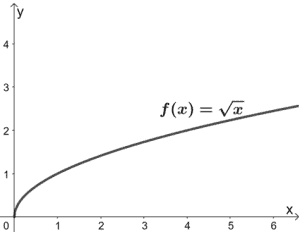
8. Welche Transformationen werden an f(x) durchgeführt, so dass g(x) = 3√(x/2) entsteht? Verwenden Sie den unten dargestellten Graphen von f(x) als Anhaltspunkt. Wenden Sie die Transformationen auf den Graphen g(x) an.

Bilder/Mathematische Zeichnungen werden mit GeoGebra erstellt.