Algebra universitaria

Per analizzare la magnitudo dei terremoti o confrontare le magnitudo di due terremoti diversi, dobbiamo essere in grado di convertire tra la forma logaritmica e quella esponenziale. Per esempio, supponiamo che la quantità di energia rilasciata da un terremoto sia 500 volte maggiore della quantità di energia rilasciata da un altro. Vogliamo calcolare la differenza di magnitudo. L’equazione che rappresenta questo problema è {10}^{x}=500 dove x rappresenta la differenza di magnitudo sulla scala Richter. Come potremmo risolvere x?

Non abbiamo ancora imparato un metodo per risolvere algebricamente le equazioni esponenziali. Nessuno degli strumenti algebrici discussi finora è sufficiente per risolvere {10}^{x}=500. Sappiamo che {10}^{2}=100 e {10}^{3}=1000, quindi è chiaro che x deve essere un valore tra 2 e 3 poiché y={10}^{x} è crescente. Possiamo esaminare un grafico per stimare meglio la soluzione.

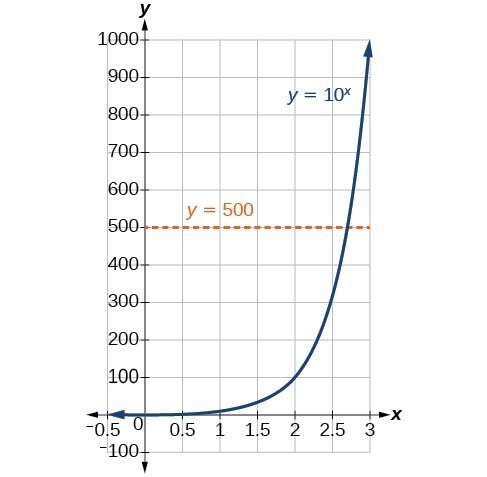
Stimare da un grafico, tuttavia, è impreciso. Per trovare una soluzione algebrica, dobbiamo introdurre una nuova funzione. Osservate che il grafico qui sopra supera il test della linea orizzontale. La funzione esponenziale y={b}^{x} è uno-a-uno, quindi anche il suo inverso, x={b}^{y} è una funzione. Come nel caso di tutte le funzioni inverse, dobbiamo semplicemente scambiare x e y e risolvere per y per trovare la funzione inversa. Per rappresentare y come funzione di x, usiamo una funzione logaritmica della forma y={mathrm{log}}_{b}{sinistra(x-destra). Il logaritmo in base b di un numero è l’esponente di cui dobbiamo elevare b per ottenere quel numero.

Leggiamo un’espressione logaritmica come: “Il logaritmo in base b di x è uguale a y” o, semplificando, “il logaritmo in base b di x è y”. Possiamo anche dire: “b elevato alla potenza di y è x”, perché i log sono esponenti. Per esempio, il logaritmo in base 2 di 32 è 5, perché 5 è l’esponente che dobbiamo applicare a 2 per ottenere 32. Poiché {2}^{5}=32, possiamo scrivere {mathrm{log}}_{2}32=5. Lo leggiamo come “il log base 2 di 32 è 5.”

Possiamo esprimere la relazione tra la forma logaritmica e la sua corrispondente forma esponenziale come segue:

{mathrm{log}}_{b}{left(x\right)=y\Leftrightarrow {b}^{y}=x,\text{}b>0,b\ne 1

Nota che la base b è sempre positiva.

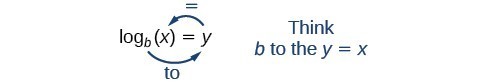
Perché un logaritmo è una funzione, è più correttamente scritto come {mathrm{log}}_{b}{sinistra(x\destra) usando le parentesi per indicare la valutazione della funzione proprio come faremmo con f\sinistra(x\destra). Tuttavia, quando l’input è una singola variabile o un numero, è comune vedere le parentesi eliminate e l’espressione scritta senza parentesi come {mathrm{log}}_{b}x. Si noti che molte calcolatrici richiedono le parentesi intorno alla x.

Possiamo illustrare la notazione dei logaritmi come segue:

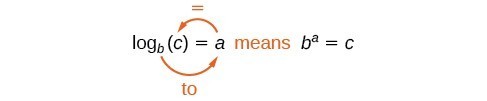
Notare che quando si confrontano la funzione logaritmo e la funzione esponenziale, l’input e l’output sono scambiati. Questo significa che y={mathrm{log}}_{b} a sinistra (x a destra) e y={b}^{x} sono funzioni inverse.

Una nota generale: definizione della funzione logaritmica

Un logaritmo base b di un numero positivo x soddisfa la seguente definizione:

Per x>0,b>0,b\ne 1,

y={mathrm{log}}_{b}left(x\right)\text{ è uguale a }{b}^{y}=x, dove

• leggiamo {mathrm{log}}_{b}left(x\destra) come, “il logaritmo con base b di x” o il “log base b di x.”
• il logaritmo y è l’esponente a cui b deve essere elevato per ottenere x.
• se non è indicata alcuna base b, si assume che la base del logaritmo sia 10.

Inoltre, poiché le funzioni logaritmica ed esponenziale scambiano i valori x e y, il dominio e l’intervallo della funzione esponenziale sono scambiati per la funzione logaritmica. Quindi,

• il dominio della funzione logaritmica con base b \testo{ è} \sinistra(0,\infty \destra).
• l’intervallo della funzione logaritmica con base b \testo{ è} \sinistra(-infty ,\infty \destra).

Q & A

Possiamo prendere il logaritmo di un numero negativo?

No. Poiché la base di una funzione esponenziale è sempre positiva, nessuna potenza di quella base può mai essere negativa. Non possiamo mai prendere il logaritmo di un numero negativo. Inoltre, non possiamo prendere il logaritmo di zero. Le calcolatrici possono produrre un logaritmo di un numero negativo quando sono in modalità complessa, ma il logaritmo di un numero negativo non è un numero reale.

Come fare: Data un’equazione in forma logaritmica {\mathrm{log}}_{b}\left(x\right)=y, convertirla in forma esponenziale

1. Esaminare l’equazione y={mathrm{log}}_{b}x e identificare b, y, e x.
2. Riscrivi {mathrm{log}}_{b}x=y come {b}^{y}=x.

Esempio: Conversione dalla forma logaritmica alla forma esponenziale

Scrivere le seguenti equazioni logaritmiche in forma esponenziale.

1. {mathrm{log}}_{6}{left(\sqrt{6}{right)=\frac{1}{2}
2. {mathrm{log}}_{3}{left(9\right)=2

Mostra soluzione

Prima, identificare i valori di b, y e x. Poi, scrivi l’equazione nella forma {b}^{y}=x.

1. {mathrm{log}}_{6}{left(\sqrt{6}{right)=\frac{1}{2} Qui, b=6,y=frac{1}{2},\testo{e} x=sqrt{6}. Pertanto, l’equazione {mathrm{log}}_{6} a sinistra(\sqrt{6} a destra)=frac{1}{2} è uguale a {6}^{frac{1}{2}}=\sqrt{6}.
2. {mathrm{log}}_{3} a sinistra(9\destra)=2 Qui, b = 3, y = 2, e x = 9. Pertanto, l’equazione {mathrm{log}}_{3}sinistra(9\destra)=2 è uguale a {3}^{2}=9.

Try It

Scrivi le seguenti equazioni logaritmiche in forma esponenziale.

1. {mathrm{log}}_{10}{sinistra(1.000,000\destra)=6
2. {mathrm{log}}}_{5}{sinistra(25\destra)=2

Mostra la soluzione

1. {mathrm{log}}_{10}{ sinistra(1,000,000)=6 è uguale a {10}^{6}=1.000,000
2. {mathrm{log}}_{5}\sinistra(25\destra)=2 è uguale a {5}^{2}=25

Convertire da forma esponenziale a logaritmica

Per convertire da forma esponenziale a logaritmica, seguiamo gli stessi passi al contrario. Identifichiamo la base b, l’esponente x e l’uscita y. Poi scriviamo x={mathrm{log}}_{b} a sinistra (y a destra).

Esempio: Conversione dalla forma esponenziale alla forma logaritmica

Scrivere le seguenti equazioni esponenziali in forma logaritmica.

1. {2}^{3}=8
2. {5}^{2}=25
3. {10}^{-4}=\frac{1}{10,000}

Mostra la soluzione

In primo luogo, identificare i valori di b, y e x. Poi, scrivi l’equazione nella forma x={mathrm{log}}_{b} a sinistra (y a destra).

1. {2}^{3}=8 Qui, b = 2, x = 3, e y = 8. Pertanto, l’equazione {2}^{3}=8 è uguale a {mathrm{log}}_{2} a sinistra(8\destra)=3.
2. {5}^{2}=25 Qui, b = 5, x = 2, e y = 25. Pertanto, l’equazione {5}^{2}=25 è uguale a {mathrm{log}}_{5} a sinistra(25\destra)=2.
3. {10}^{-4}=\frac{1}{10.000} Qui, b = 10, x = -4, e y=\frac{1}{10.000}. Pertanto, l’equazione {10}^{-4}=\frac{1}{10.000} è uguale a {\testo{log}}_{10} a sinistra(\frac{1}{10.000} a destra)=-4.

Try It

Scrivi le seguenti equazioni esponenziali in forma logaritmica.

1. {3}^{2}=9
2. {5}^{3}=125
3. {2}^{-1}=\frac{1}{2}

Mostra soluzione

1. {3}^{2}=9 è uguale a {mathrm{log}}_{3} a sinistra(9\destra)=2
2. {5}^{3}=125 è uguale a {mathrm{log}}_{5} a sinistra(125\destra)=3
3. {2}^{-1}=frac{1}{2} è uguale a {testo{log}}_{2} a sinistra(\frac{1}{2} a destra)=-1

Contribuisci!

Hai un’idea per migliorare questo contenuto? Ci piacerebbe avere il tuo contributo.

Migliorare questa paginaPer saperne di più