Quando si inseriscono valori numerici nei campi di risposta, è possibile utilizzare numeri interi (1000, 0x3E8, 0b1111101000), numeri in virgola mobile (1000.0), notazione scientifica (1e3), fattori di scala ingegneristici (1K), o espressioni numeriche (3*300 + 100).Link utili:
- Introduzione a Jade
- Standard Cell Library
Problema 1. Problema di progettazione: 32-bit Arithmetic and Logic UnitVedi le istruzioni qui sotto.Usa l’istanza Jade qui sotto per inserire il tuo progetto. Per completare questo problema di progettazione, selezionate il modulo /alu/alu e cliccate nella barra degli strumenti Jade e il tester incorporato riporterà eventuali discrepanze tra le uscite previste e quelle effettive, oppure, se il vostro progetto è corretto, registrerà il test superato.{ “shared_modules”: , “hierarchical”: “true”, “parts” , “strumenti”: , “editor”: , “edit”: “/alu/alu”, “required_tests”: }In questo laboratorio, costruiremo l’unità aritmetica e logica (ALU) per il processore Beta. L’ALU ha due ingressi a 32 bit (che chiameremo “A” e “B”) e produce un’uscita a 32 bit. Inizieremo progettando ogni pezzo dell’ALU come un circuito separato, ognuno dei quali produce la propria uscita a 32 bit. Poi combineremo queste uscite in un singolo risultato ALU.Quando si progetta un circuito ci sono tre fattori separati che possono essere ottimizzati:
- progettare per la massima prestazione (minima latenza)
- progettare per il minimo costo (minima area)
- progettare per il miglior rapporto costo/prestazioni (minimizzare area*latenza)
Fortunatamente è spesso possibile fare tutte e tre le cose insieme ma in alcune porzioni del circuito qualche tipo di compromesso progettuale dovrà essere fatto. Quando progettate il vostro circuito dovreste scegliere quale dei tre fattori è più importante per voi e ottimizzare il vostro design di conseguenza. La libreria di celle standard & simulazione a livello di gateI blocchi di costruzione per questo laboratorio provengono da una libreria di logicgates – i produttori di IC spesso hanno una “libreria di celle standard” e vari strumenti di progettazione per rendere più facile per i loro clienti progettare senza preoccuparsi della geometria dettagliata degli strati della maschera usati per creare i mosfet e il cablaggio. 6.004 ha la propriaStandard Cell Libraryche fornisce:
inverter, buffer, tristate driver
gate AND, OR, NAND e NOR a 2, 3 e 4 ingressi
gate XOR e XNOR a 2 ingressi
multiplexor 2:1 e 4:1
D-register e D-latches
Vedi la documentazione della libreria per i dettagli sulle connessioni appropriate per ogni gate. In Jade, i gate della libreria di celle standard possono essere trovati nel contenitore delle parti sotto “/gates/”.
Dato che stiamo progettando a livello di gate possiamo usare un fastersimulator che conosce solo i gate e i valori logici (invece di transistor e tensioni). Notate che il vostro progetto non può contenere alcunmosfet, resistenze, condensatori, ecc.; il simulatore a livello di gate supporta solo le primitive di gate nella libreria standard delle celle.Gli ingressi sono ancora specificati in termini di tensioni (per mantenere la compatibilità con gli altri simulatori) ma il simulatore di gate-levels converte le tensioni in uno dei tre possibili valori logici utilizzando le soglie vil e vih specificate all’inizio del vostro file di progetto:
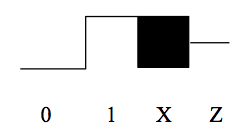
0 logico basso (tensioni minori o uguali alla soglia vil)
1 logico alto (tensioni maggiori o uguali alla soglia vih)
X sconosciuto o indefinito (tensioni tra le soglie, o tensioni sconosciute)
Un quarto valore “Z” è usato per rappresentare il valore dei nodi che non sono pilotati da nessuna uscita del gate (es.g., le uscite dei tristati che non sono abilitati). Il seguente diagramma mostra come questi valori appaiono sul display della forma d’onda:
Specifiche ALU
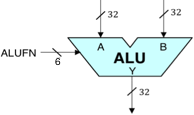
La ALU a 32 bit che costruiremo sarà un componente del Betaprocessore che affronteremo nei laboratori successivi. Il simbolo logico della nostra ALU è mostrato a destra. È un circuito combinazionale che prende due parole di dati a 32 bit A e B come ingressi, e produce un’uscita a 32 bit Y eseguendo una specifica funzione aritmetica o logica sugli ingressi A e B. La particolare funzione da eseguire è specificata da un ingresso di controllo a 6 bit, FN, il cui valore codifica la funzione secondo la seguente tabella:
| FN |
Operazione |
Valore in uscita Y |
| 00-011 |
CMPEQ |
Y = (A == B) |
| |
00-101 |
CMPLT |
Y = (A < B) |
| 00-111 |
CMPLE |
Y = (A ≤ B) |
| 01—0 |
32-bit ADD |
Y = A + B |
| 01—1 |
32-bit SUBTRACT |
Y = A – B |
| |
10abcd |
Bit-wise Boolean |
Y = Fabcd(A,B) |
| 11–00 |
Spostamento logico a sinistra (SHL) |
Y = A << B |
| 11–01 |
Spostamento logico a destra (SHR) |
Y = A >> B |
| 11–11 |
Spostamento aritmetico a destra (SRA) |
Y = A >> B (segno esteso) |
Si noti che specificando un valore appropriato per il 6-bit FNinput, l’ALU può eseguire una varietà di operazioni aritmetiche, confronti, spostamenti e combinazioni booleane bitwise richieste dal nostro processore Beta.
| |
Bi |
Ai |
Yi |
| 0 |
0 |
d |
| 0 |
1 |
c |
| 1 |
0 |
b |
| 1 |
1 |
a |
Le operazioni booleane bitwise sono specificate da FN=10; in questo caso, i rimanenti bit FN abcd sono presi come voci nella tabella di verità che descrive come ogni bit di Y è determinato dai bit corrispondenti di A e B, come mostrato a destra.Le tre operazioni di confronto producono ciascuna un’uscita booleana. In questi casi, Y sono tutti zero, e il bit di ordine inferiore Y è uno 0 o un 1 che riflette il risultato del confronto tra gli operandi A e B a 32 bit.Possiamo avvicinarci alla progettazione dell’ALU suddividendola in sottosistemi dedicati alle operazioni aritmetiche, di confronto, booleane e di shift come mostrato di seguito:
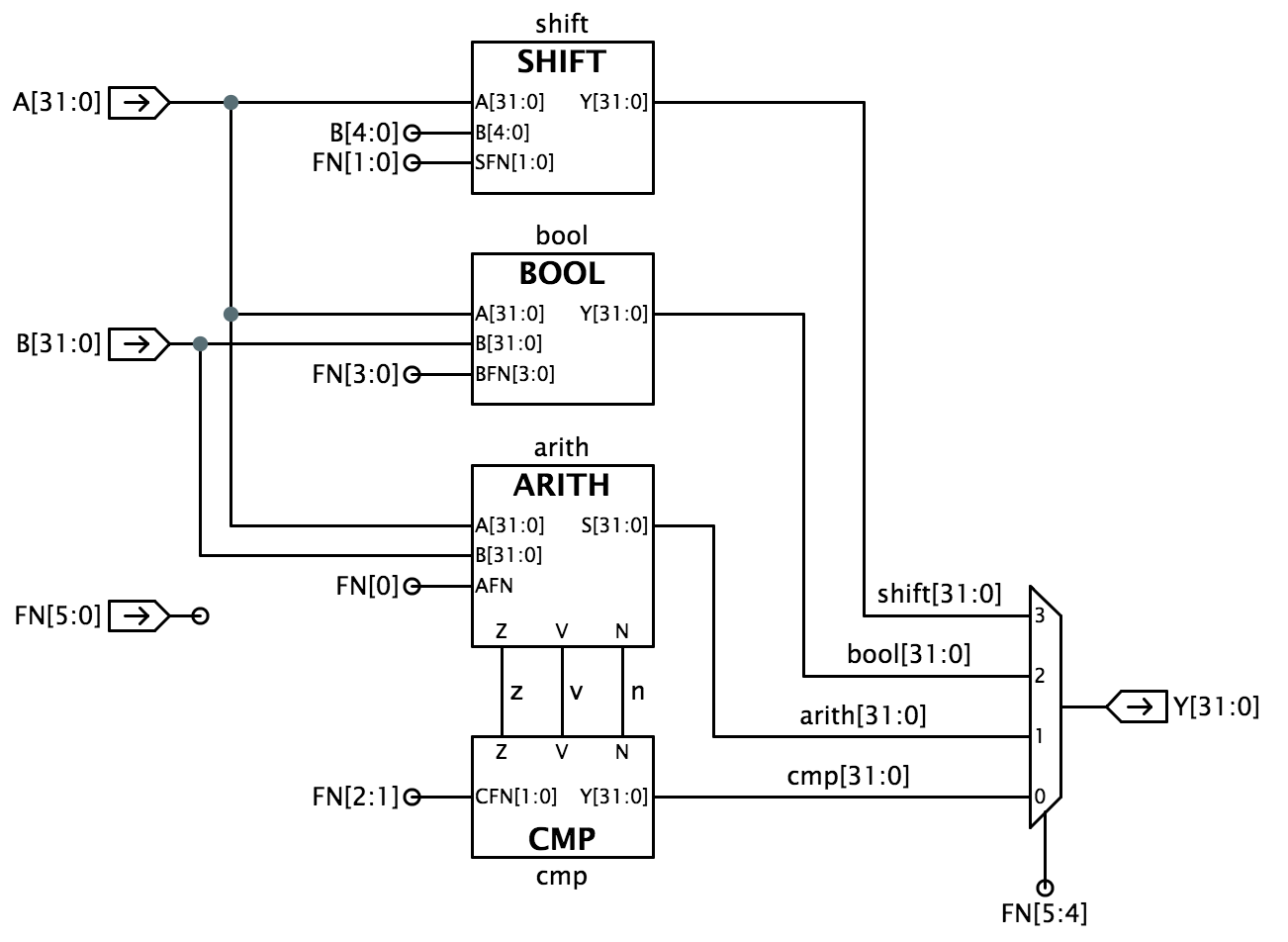
Progettare un sistema complesso come una ALU è meglio farlo per gradi, permettendo ai singoli sottosistemi di essere progettati e debuggati uno alla volta. I passi che seguono seguono questo approccio per implementare il diagramma di ALUblock mostrato sopra. Iniziamo implementando un ALUframework con moduli fittizi per ognuno dei quattro principali sottosistemi (BOOL, ARITH, CMP, e SHIFT); poi implementiamo e debuggiamo le versioni funzionanti di ogni sottosistema. Per aiutarvi a seguire questo percorso, forniamo test separati per ciascuno dei quattro moduli componenti.NOTA: i segnali FN usati per controllare il funzionamento dell’ALUcircuitry usano una codifica scelta per rendere semplice la progettazione dell’ALUcircuitry. Questa codifica non è la stessa usata per codificare il campo opcode a 6 bit delle istruzioni Beta. Nel laboratorio 5, costruirete una logica (in realtà una ROM) che tradurrà il campo opcode di un’istruzione nei bit di controllo FN appropriati. Ci sono note di progettazione qui sotto che suggeriscono come procedere nella progettazione di ciascuno dei sottomoduli. Unità BOOL Progettate il circuito per implementare le operazioni booleane per la vostra ALU e usatelo per sostituire il ponticello e il filo che collega l’uscita a terra.
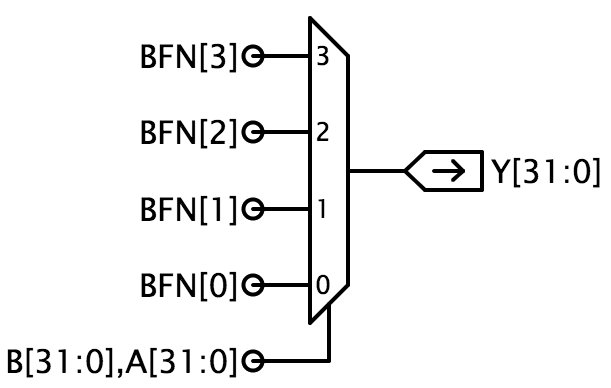
L’implementazione suggerita usa 32 copie di un multiplexor 4-to-1 (mux4) dove BFN codifica l’operazione da eseguire e A e B sono agganciati agli ingressi di selezione del multiplexor. Questa implementazione può produrre una qualsiasi delle 16 funzioni booleane a 2 ingressi.
Suggerimento: Jade replicherà automaticamente una porta logica per far corrispondere la larghezza degli ingressi e delle uscite della porta alla larghezza dei segnali che si connettono alla porta. Per esempio, il gate MUX4 mostrato sopra ha un segnale di uscita a 1 bit, che in questo schema è agganciato a Y, un segnale di larghezza 32. Quindi Jade replicherà il MUX4 32 volte, l’uscita del primo MUX4 si collega a Y, l’uscita del secondo MUX4 si collega a Y, e così via. I segnali di ingresso sono poi replicati (se necessario) per fornire gli ingressi per ciascuno dei 32 gate MUX4. Ogni porta MUX4 richiede 2 segnali di selezione, che sono presi dai 64 segnali forniti. B e A si collegano alle linee di selezione del primo MUX4, B e A si collegano alle linee di selezione del secondo MUX4, e così via. Ogni porta MUX4 richiede 4 segnali di dati. Gli ingressi BFN specificati sono larghi solo 1 bit, quindi i segnali specificati sono ciascuno replicato 32 volte, ad esempio, BFN è usato come ingresso D0 per ciascuno dei 32 MUX4.
La seguente tabella mostra le codifiche per alcuni dei segnali di controllo BFN usati dalla maschera di prova (e nelle nostre tipiche Betaimplementazioni):
| Operazione |
BFN |
| AND |
1000 |
| OR |
1110 |
| XOR |
0110 |
| “A” |
1010 |
Il test BOOL controlla effettivamente tutte le 16 operazioni booleane su una selezione di argomenti, e riporterà tutti gli errori che trova.Quando il vostro circuito BOOL è stato inserito, eseguite il test cliccando sul segno di spunta verde; dovrebbe apparire una finestra di simulazione che mostra gli ingressi e le uscite. Jade controllerà i risultati del vostro circuito rispetto a una lista di valori attesi e riporterà qualsiasi discrepanza che trova.
Suggerimento: cosa faccio quando la verifica fallisce? La notifica di fallimento ti dirà quale segnale ha fallito la verifica e il tempo simulato in cui si è verificata la discrepanza tra il valore reale e quello atteso. I test sono in realtà una sequenza di cicli di verifica di 100ns e il tempo riportato sarà alla fine di uno dei cicli quando i valori di uscita sono controllati per la correttezza. Muovete il mouse sul grafico della forma d’onda del segnale appropriato fino a quando il cursore verticale del tempo si trova approssimativamente sul tempo di guasto. Poi fate doppio clic per ingrandire i grafici intorno a quel particolare momento; ingrandite abbastanza in modo che tutti i segnali per quel ciclo di test siano leggibili. Ora puoi capire cosa è stato chiesto al circuito per quel particolare test e, si spera, dedurre perché il tuo circuito sta producendo un’uscita errata.
Unità ARITHProgetta un’unità addizionatrice/sottrattore (ARITH) che opera su ingressi di complemento a due bit e genera un’uscita a 32 bit. Sarà utile generare altri tre segnali di uscita da utilizzare per l’unità CMP: Z che è vero quando le uscite S sono tutte zero, V che è vero quando l’operazione di addizione trabocca (cioè, il risultato è troppo grande per essere rappresentato in 32 bit), e N che è vero quando la somma è negativa (cioè, S = 1).L’overflow non può mai verificarsi quando i due operandi dell’addizione hanno segni diversi; se i due operandi hanno lo stesso segno, allora l’overflow può essere rilevato se il segno del risultato differisce dal segno degli operandi:
\(V = XA_{31}\cdot XB_{31}\cdot \overline{S_{31} + \overline{XA_{31}}{XB_{31}}{B_{31})Si noti che questa equazione usa XB, che è il bit di ordine superiore dell’operando B dell’addizionatore stesso (cioè, dopo la porta XOR – vedi lo schema sotto). XA è semplicemente A. Il seguente schema è un suggerimento su come procedere nella progettazione:

AFN sarà impostato a 0 per un ADD (\(S = A+B\)) e 1 per un SUBTRACT (\(S = A-B\)); A e B sono gli operandi di ingresso a 32 bit di complemento a due; S è il risultato a 32 bit; Z/V/N sono i tre codebits di condizione descritti sopra. Useremo la convenzione di numerazione dei bit “little-endian” dove il bit 31 è il bit più significativo e il bit 0 è il bit meno significativo. Abbiamo fornito un modulo FA per inserire lo schema a livello di gate per l’addizionatore completo (vedi Problema 8 del Laboratorio #1) da usare nella costruzione dell’addizionatore ripple carry a 32 bit che forma il cuore dell’unità ARITH. Il segnale d’ingresso AFN seleziona se l’operazione è un ADD o un SUBTRACT. Per fare un SUBTRACT, il circuito prima calcola la negazione del complemento a due dell’operando B invertendo B e poi aggiungendo uno (che può essere fatto forzando il carry-in dell’add a 32 bit ad essere 1). Iniziate ad implementare l’addizione a 32 bit usando un’architettura aripple-carry (migliorerete questo aspetto più avanti nel corso). Dovrete costruire la porta NOR a 32 ingressi necessaria per calcolare Z usando un albero di porte a ventola più piccole (la libreria delle parti ha solo porte con un massimo di 4 ingressi). Quando inserite il vostro circuito, ricordatevi di eliminare i ponticelli e i fili originali che collegavano le uscite a terra! Il test del modulo prova ad aggiungere e sottrarre vari operandi, assicurandosi che le uscite Z, V e N siano corrette dopo ogni operazione. Unità CMPL’ALU fornisce tre operazioni di confronto per gli operandi A e B. Possiamo usare l’unità sommatrice progettata sopra per calcolare \(A-B\)e poi guardare il risultato (in realtà solo i codici di condizione Z, V e N) per determinare se A=B, A < B o A ≤ B. Le operazioni di confronto generano un risultato a 32 bit usando il numero 0 per rappresentarefalso e il numero 1 per rappresentare vero.Progettate un’unità di confronto a 32 bit (CMP) che genera una delle due costanti (0 o 1) a seconda dei segnali di controllo CFN (usati per selezionare il confronto da eseguire) e delle uscite Z, V e N dell’unità sommatore/sottrattore. Chiaramente i 31 bit di ordine superiore dell’uscita sono sempre zero. Il bit meno significativo (LSB) dell’uscita è determinato dal confronto eseguito e dai risultati della sottrazione effettuata dall’addizionatore/sottrattore:
| Confronto |
Equazione per LSB |
CFN |
| A = B |
LSB = \(Z\) |
01 |
| A < B |
LSB = \(N \plus V) |
10 |
| A ≤ B |
LSB = \(Z + (N \plus V)\) |
11 |
A livello del modulo ALU, FN sono usati per controllare l’unità di confronto poiché abbiamo bisogno di usare FN per controllare l’unità adder/subtractor per forzare una sottrazione.Nota sulle prestazioni: gli ingressi Z, V e N di questo circuito possono essere calcolati dall’unità adder/subtractor solo dopo che l’addizione a 32 bit è completata. Questo significa che arrivano abbastanza tardi e richiedono un’ulteriore elaborazione in questo modulo, che a sua volta fa apparire Y molto tardi nel gioco. Potete accelerare considerevolmente le cose pensando alla tempistica relativa di Z, V e N e poi progettando la vostra logica per minimizzare i percorsi di ritardo che coinvolgono i segnali che arrivano in ritardo.Il test del modulo assicura che la risposta corretta sia generata per tutte le possibili combinazioni di Z, V, N e CFN. SHIFT unitDesign uno shifter a 32 bit che implementa le operazioni di spostamento logico a sinistra (SHL), spostamento logico a destra (SHR) e spostamento aritmetico a destra (SRA).L’operando A fornisce i dati da spostare e i 5 bit di ordine inferiore dell’operando B sono usati come conteggio dello spostamento (cioè, da 0 a 31 bit di spostamento). L’operazione desiderata sarà codificata su SFN come segue:
| Operazione |
SFN |
| SHL (shift left) |
00 |
| SHR (shift destra) |
01 |
| SRA (shift a destra con estensione del segno) |
11 |
Con questa codifica, SFN è 0 per uno spostamento a sinistra e 1 per uno spostamento a destra e SFN controlla la logica di estensione del segno sullo spostamento a destra. Per SHL e SHR, gli 0 sono spostati nelle posizioni di bit libere. Per SRA (“shift right arithmetic”), le posizioni di bit libere sono tutte riempite con A, il bit di segno del dato originale in modo che il risultato sia lo stesso che dividendo i dati originali per la potenza appropriata di 2. L’implementazione più semplice è costruire due shifter – uno per lo shift a sinistra e uno per lo shift a destra – e poi usare un multiplexer a 2 vie da 32 bit per selezionare la risposta appropriata come uscita del modulo. È facile costruire un traslatore dopo aver notato che uno spostamento a più bit può essere realizzato con spostamenti in cascata di varie potenze di 2. Per esempio, uno spostamento di 13 bit può essere implementato da uno spostamento di 8, seguito da uno spostamento di 4, seguito da uno spostamento di 1. Quindi il traslatore è solo una cascata di multiplexer ognuno controllato da un bit del conteggio dello spostamento. Lo schema qui sotto mostra una possibile implementazione della logica di spostamento di sinistra; la logica di spostamento di destra è simile con la leggera complicazione aggiunta di dover spostare o 0 (cioè, “gnd”) o A, a seconda del valore diSFN. Un altro approccio che risparmia le porte è quello di usare la logica leftshift per entrambi gli spostamenti a sinistra e a destra, ma per gli spostamenti a destra, invertire i bit dell’operando A all’entrata e invertire i bit dell’uscita all’uscita.
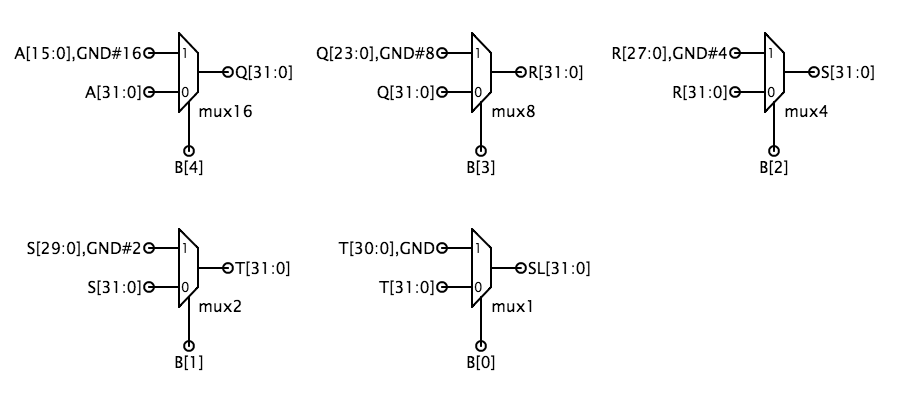
Il test del modulo controlla che tutti e tre i tipi di spostamento funzionino correttamente. Test finaliQuando avete completato la progettazione dei quattro sottomoduli, selezionate il modulo ALU ed eseguite il suo test. Questo esegue ciascuno dei test che avete usato per il debug dei sottocircuiti dei componenti, quindi, a meno che non ci sia qualche interazione imprevista tra i vostri blocchi, è probabile che il test venga superato. Quando questo test si completa con successo, il sistema segnerà il vostro progetto come completo. Problema 2. Test dell’ALUNel problema di progettazione di questo laboratorio (vedi sopra), costruirai un’unità aritmetica e logica (ALU) a 32 bit che esegue operazioni aritmetiche e logiche su operandi a 32 bit, producendo un risultato a 32 bit. Il test per questo laboratorio verifica il tuo circuito ALU applicando 186 diversi set di valori di ingresso. Questa domanda esplora come sono stati scelti quei valori.Nessun progettista che io conosca pensa che il test sia divertente – progettare il circuito sembra molto più interessante che assicurarsi che funzioni.Ma anche un progetto difettoso non è molto divertente! Ricordate che un buon ingegnere non solo sa come costruire buoni progetti, ma costruisce anche buoni progetti, e questo significa testare il progetto per assicurarsi che faccia quello che dite che fa. Un modo ovvio per testare un circuito combinatorio è provare tutte le possibili combinazioni di ingressi, controllando i valori di uscita corretti dopo aver applicato ogni combinazione di ingressi. Questo tipo di test esaustivo prova il corretto funzionamento enumerando la tabella di verità del dispositivo combinatorio. Questa è una strategia di lavoro per circuiti con pochi ingressi, ma diventa rapidamente pratica per circuiti con molti ingressi. Sfruttando le informazioni su come è costruito il circuito possiamo ridurre notevolmente il numero di combinazioni di ingressi necessarie per testare il circuito.L’architettura dell’addizionatore ripple-carry suggerita nel Problema di progettazione usa 32 copie del modulo dell’addizionatore completo per creare un addizionatore a 32 bit.Ogni addizionatore completo ha 3 ingressi (A, B, CI) e due uscite (S, CO):
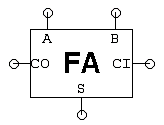
- Un singolo vettore di test per l’adder completo consiste in 3 valori di ingresso (uno ciascuno per A, B e CI) e 2 valori di uscita (S e CO). Per eseguire un test, i valori di ingresso dal vettore di test corrente vengono applicati al dispositivo in prova e poi i valori di uscita effettivi vengono confrontati con i valori previsti elencati dal vettore di test. Questo processo viene ripetuto fino a quando tutti i vettori di test sono stati utilizzati. Supponendo di non sapere nulla del circuito interno dell’addizionatore completo, di quanti vettori di test avremmo bisogno per testare esaustivamente la sua funzionalità? Numero di vettori di test per testare in modo esaustivo l’adduttore completo?
- Consideriamo un sommatore a 32 bit con 64 ingressi (due operandi di ingresso a 32 bit, assumiamo che CIN sia legato a terra come mostrato nel diagramma qui sotto) e 32 uscite (il risultato a 32 bit). Supponiamo di non sapere nulla del circuito interno e quindi non possiamo escludere la possibilità che possa ottenere la risposta sbagliata per qualsiasi combinazione particolare di ingressi. In altre parole, solo perché l’addizionatore ha ottenuto la risposta corretta per 2 + 3 non ci permette di trarre alcuna conclusione su quale risposta avrebbe ottenuto per 2 + 7. Se potessimo applicare un vettore di test ogni 100ns, quanto tempo ci vorrebbe per testare esaustivamente l’addizionatore? Tempo per testare esaustivamente l’addizionatore a 32 bit? (in anni)
- E’ chiaro che testare un sommatore a 32 bit provando tutte le combinazioni di valori di ingresso non è un buon piano! Di seguito è mostrato uno schema per un sommatore a 32 bit ripple-carry.
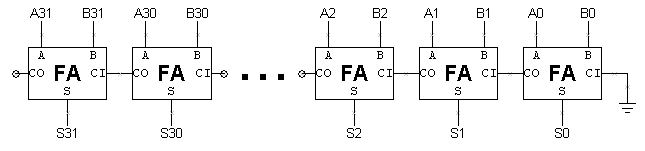 Ad eccezione del carry-in dal bit a destra, ogni bit dell’addizionatore funziona indipendentemente. Possiamo usare questa osservazione per testare l’addizionatore bit per bit e con un po’ di riflessione possiamo effettivamente eseguire molti di questi test in parallelo. In questo caso il fatto che l’addizionatore abbia ottenuto la risposta corretta per 2 + 3 in realtà ci dice molto sulla risposta che otterrà per 2 + 7. Poiché il calcolo fatto dai bit 0 e 1 dell’addizionatore è lo stesso in entrambi i casi, se la risposta per 2 + 3 è corretta, anche i due bit di ordine inferiore della risposta per 2 + 7 saranno corretti. Quindi il nostro piano per testare il sommatore ripple-carry è di testare ogni sommatore completo in modo indipendente. Quando testiamo il bit N possiamo impostare A e B direttamente dal vettore di test. Ci vuole un po’ più di lavoro per impostare CI ad un particolare valore, ma possiamo farlo con le scelte corrette per A e B. Se vogliamo impostare CI a 0, a quali valori dovrebbero essere impostati A e B? Se vogliamo impostare CI a 1? Supponiamo di non poter supporre nulla sul valore di CI. Valori di A e B per rendere C=0? A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 Valori di A e B per fare C=1? A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 Con questa strategia possiamo testare i bit pari dell’addizionatore in parallelo con un set di vettori di test e testare i bit dispari dell’addizionatore in parallelo con un altro set di vettori di test. Ecco una serie di 10 vettori di test che dovrebbero testare tutte le combinazioni di valori di ingresso per ogni FA in un sommatore ripple-carry a 32 bit:
Ad eccezione del carry-in dal bit a destra, ogni bit dell’addizionatore funziona indipendentemente. Possiamo usare questa osservazione per testare l’addizionatore bit per bit e con un po’ di riflessione possiamo effettivamente eseguire molti di questi test in parallelo. In questo caso il fatto che l’addizionatore abbia ottenuto la risposta corretta per 2 + 3 in realtà ci dice molto sulla risposta che otterrà per 2 + 7. Poiché il calcolo fatto dai bit 0 e 1 dell’addizionatore è lo stesso in entrambi i casi, se la risposta per 2 + 3 è corretta, anche i due bit di ordine inferiore della risposta per 2 + 7 saranno corretti. Quindi il nostro piano per testare il sommatore ripple-carry è di testare ogni sommatore completo in modo indipendente. Quando testiamo il bit N possiamo impostare A e B direttamente dal vettore di test. Ci vuole un po’ più di lavoro per impostare CI ad un particolare valore, ma possiamo farlo con le scelte corrette per A e B. Se vogliamo impostare CI a 0, a quali valori dovrebbero essere impostati A e B? Se vogliamo impostare CI a 1? Supponiamo di non poter supporre nulla sul valore di CI. Valori di A e B per rendere C=0? A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 Valori di A e B per fare C=1? A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 Con questa strategia possiamo testare i bit pari dell’addizionatore in parallelo con un set di vettori di test e testare i bit dispari dell’addizionatore in parallelo con un altro set di vettori di test. Ecco una serie di 10 vettori di test che dovrebbero testare tutte le combinazioni di valori di ingresso per ogni FA in un sommatore ripple-carry a 32 bit:
| bits 0, 2, … |
bits 1, 3, … |
A |
B |
| A=0, B=0, CI=0 |
A=0, B=0, CI=0 |
0x00000000 |
0x00000000 |
| A=1, B=0, CI=0 |
A=0, B=0, CI=0 |
0x55555555 |
0x00000000 |
| A=0, B=1, CI=0 |
A=0, B=0, CI=0 |
0x00000000 |
0x555555 |
| A=1, B=1, CI=0 |
A=0, B=0, CI=1 |
0x555555 |
0x555555 |
| A=0, B=0, CI=0 |
A=1, B=0, CI=0 |
0xAAAAAA |
0x00000000 |
| A=0, B=0, CI=0 |
A=0, B=1, CI=0 |
0x00000000 |
0xAAAAAA |
| A=0, B=0, CI=1 |
A=1, B=1, CI=0 |
0xAAAAAAAA |
0xAAAA |
| A=1, B=0, CI=1 |
A=1, B=0, CI=1 |
0xFFFFFFFFFFFF |
0x00000001 |
| A=0, B=1, CI=1 |
A=0, B=1, CI=1 |
0x00000001 |
0xFFFFFFFFFF |
| A=1, B=1, CI=1 |
A=1, B=1, CI=1 |
0xFFFFFFFFFF |
0xFFFFFFFFFF |
- Tre degli ingressi dell’unità di confronto (Z, V e N) provengono dall’adder/sottrattore che funziona in modalità sottrazione calcolando A-B:
Z = 1 se A-B è 0 N = 1 se A-B è negativo (OUT = 1) V = 1 se c’è stato un overflow. L’ALU, che ha solo un sommatore, calcola A-B come A+(-B) = A+(~B)+1. Sia XB = ~B, il complemento bit-wise di B. Un overflow si verifica se il segno del risultato (OUT) differisce dai segni degli operandi dell’addizionatore (A, XB). Si noti che se i segni di A e XB differiscono, l’addizione non può produrre un overflow.Per testare l’unità di confronto, avremo bisogno di scegliere operandi per l’addizionatore/sottrattore che generino tutte le possibili combinazioni di Z, V e N. È facile vedere che qualsiasi combinazione con Z = 1 e N = 1 non è possibile (l’uscita dell’addizionatore non può essere negativa e zero allo stesso tempo!) Si scopre anche che le combinazioni con Z = 1 e V = 1 non possono essere prodotte da un’operazione di sottrazione. Per ciascuna delle combinazioni di Z, V e N mostrate qui sotto, scegliete l’operazione di sottrazione che produrrà la combinazione specificata di codici condizione. Sottrazione che produce Z=0, V=0, N=0? 0x12345678 – 0x12345678 0x7FFFFFFF – 0xFFFFFFFFFF 0x00000005 – 0xDEADBEEF 0xDEADBEEF – 0x00000005 0x80000000 – 0x00000001 Sottrazione che produce Z=1, V=0, N=0? 0x12345678 – 0x12345678 0x7FFFFFFFFF – 0xFFFFFFFFFF 0x00000005 – 0xDEADBEEF 0xDEADBEEF – 0x00000005 0x80000000 – 0x00000001 Sottrazione che produce Z=0, V=1, N=0? 0x12345678 – 0x12345678 0x7FFFFFFFFF – 0xFFFFFFFFFF 0x00000005 – 0xDEADBEEF 0xDEADBEEF – 0x00000005 0x80000000 – 0x00000001 Sottrazione che produce Z=0, V=0, N=1? 0x12345678 – 0x12345678 0x7FFFFFFFFF – 0xFFFFFFFFFF 0x00000005 – 0xDEADBEEF 0xDEADBEEF – 0x00000005 0x80000000 – 0x00000001 Sottrazione che produce Z=0, V=1, N=1? 0x12345678 – 0x12345678 0x7FFFFFFFFF – 0xFFFFFFFFFF 0x00000005 – 0xDEADBEEF 0xDEADBEEF – 0x00000005 0x80000000 – 0x00000001 Problema 3. L’unità versatile BOOL
| Bi |
Ai |
Yi |
| 0 |
0 |
d |
| 0 |
1 |
c |
| 1 |
0 |
b |
| 1 |
1 |
a |
Come abbiamo visto nelle istruzioni dell’ALU,le operazioni booleane bitwise sono specificate da FN=10. In questo caso, i rimanenti bit FN abcd sono presi come voci nella tabella della verità che descrive come ogni bit di Y sia determinato dai corrispondenti bit di A e B, come mostrato a destra.Per ciascuna delle operazioni booleane \(F(A,B)\) specificate di seguito, determinate le impostazioni per FN in modo che l’unità Bool computi l’operazione desiderata. AND(A,B): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 OR(A,B): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 XOR(A,B): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 NAND(A,B): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 111111 NOR(A,B): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 XNOR(A,B): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 A: FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 B: FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

 La ALU a 32 bit che costruiremo sarà un componente del Betaprocessore che affronteremo nei laboratori successivi. Il simbolo logico della nostra ALU è mostrato a destra. È un circuito combinazionale che prende due parole di dati a 32 bit A e B come ingressi, e produce un’uscita a 32 bit Y eseguendo una specifica funzione aritmetica o logica sugli ingressi A e B. La particolare funzione da eseguire è specificata da un ingresso di controllo a 6 bit, FN, il cui valore codifica la funzione secondo la seguente tabella:
La ALU a 32 bit che costruiremo sarà un componente del Betaprocessore che affronteremo nei laboratori successivi. Il simbolo logico della nostra ALU è mostrato a destra. È un circuito combinazionale che prende due parole di dati a 32 bit A e B come ingressi, e produce un’uscita a 32 bit Y eseguendo una specifica funzione aritmetica o logica sugli ingressi A e B. La particolare funzione da eseguire è specificata da un ingresso di controllo a 6 bit, FN, il cui valore codifica la funzione secondo la seguente tabella:

 L’implementazione suggerita usa 32 copie di un multiplexor 4-to-1 (mux4) dove BFN codifica l’operazione da eseguire e A e B sono agganciati agli ingressi di selezione del multiplexor. Questa implementazione può produrre una qualsiasi delle 16 funzioni booleane a 2 ingressi.
L’implementazione suggerita usa 32 copie di un multiplexor 4-to-1 (mux4) dove BFN codifica l’operazione da eseguire e A e B sono agganciati agli ingressi di selezione del multiplexor. Questa implementazione può produrre una qualsiasi delle 16 funzioni booleane a 2 ingressi.



 Ad eccezione del carry-in dal bit a destra, ogni bit dell’addizionatore funziona indipendentemente. Possiamo usare questa osservazione per testare l’addizionatore bit per bit e con un po’ di riflessione possiamo effettivamente eseguire molti di questi test in parallelo. In questo caso il fatto che l’addizionatore abbia ottenuto la risposta corretta per 2 + 3 in realtà ci dice molto sulla risposta che otterrà per 2 + 7. Poiché il calcolo fatto dai bit 0 e 1 dell’addizionatore è lo stesso in entrambi i casi, se la risposta per 2 + 3 è corretta, anche i due bit di ordine inferiore della risposta per 2 + 7 saranno corretti. Quindi il nostro piano per testare il sommatore ripple-carry è di testare ogni sommatore completo in modo indipendente. Quando testiamo il bit N possiamo impostare A e B direttamente dal vettore di test. Ci vuole un po’ più di lavoro per impostare CI ad un particolare valore, ma possiamo farlo con le scelte corrette per A e B. Se vogliamo impostare CI a 0, a quali valori dovrebbero essere impostati A e B? Se vogliamo impostare CI a 1? Supponiamo di non poter supporre nulla sul valore di CI. Valori di A e B per rendere C=0? A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 Valori di A e B per fare C=1? A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 Con questa strategia possiamo testare i bit pari dell’addizionatore in parallelo con un set di vettori di test e testare i bit dispari dell’addizionatore in parallelo con un altro set di vettori di test. Ecco una serie di 10 vettori di test che dovrebbero testare tutte le combinazioni di valori di ingresso per ogni FA in un sommatore ripple-carry a 32 bit:
Ad eccezione del carry-in dal bit a destra, ogni bit dell’addizionatore funziona indipendentemente. Possiamo usare questa osservazione per testare l’addizionatore bit per bit e con un po’ di riflessione possiamo effettivamente eseguire molti di questi test in parallelo. In questo caso il fatto che l’addizionatore abbia ottenuto la risposta corretta per 2 + 3 in realtà ci dice molto sulla risposta che otterrà per 2 + 7. Poiché il calcolo fatto dai bit 0 e 1 dell’addizionatore è lo stesso in entrambi i casi, se la risposta per 2 + 3 è corretta, anche i due bit di ordine inferiore della risposta per 2 + 7 saranno corretti. Quindi il nostro piano per testare il sommatore ripple-carry è di testare ogni sommatore completo in modo indipendente. Quando testiamo il bit N possiamo impostare A e B direttamente dal vettore di test. Ci vuole un po’ più di lavoro per impostare CI ad un particolare valore, ma possiamo farlo con le scelte corrette per A e B. Se vogliamo impostare CI a 0, a quali valori dovrebbero essere impostati A e B? Se vogliamo impostare CI a 1? Supponiamo di non poter supporre nulla sul valore di CI. Valori di A e B per rendere C=0? A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 Valori di A e B per fare C=1? A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 Con questa strategia possiamo testare i bit pari dell’addizionatore in parallelo con un set di vettori di test e testare i bit dispari dell’addizionatore in parallelo con un altro set di vettori di test. Ecco una serie di 10 vettori di test che dovrebbero testare tutte le combinazioni di valori di ingresso per ogni FA in un sommatore ripple-carry a 32 bit: