Chang Hsin Lee

Quando costruisco un modello di apprendimento automatico per problemi di classificazione, una delle domande che mi faccio è perché il mio modello non fa schifo? A volte sento che sviluppare un modello è come tenere in mano una granata, e la calibrazione è una delle mie spille di sicurezza. In questo post, passerò attraverso il concetto di calibrazione, poi mostrerò in Python come fare grafici diagnostici di calibrazione.

Qui c’è il link al notebook Jupyter per questo post

Valutazione delle previsioni probabilistiche

Inizio spiegando cos’è la calibrazione e da dove viene l’idea.

Nel machine learning, la maggior parte dei modelli di classificazione producono previsioni di probabilità di classe tra 0 e 1, quindi hanno un’opzione per trasformare gli output probabilistici in previsioni di classe. Anche gli algoritmi che producono solo punteggi, come le support vector machine, possono essere adattati per produrre previsioni probabilistiche.

Per un problema di classificazione binaria, ci sono metriche riassuntive – accuratezza, precisione, richiamo, F1-score, e così via – che valutano la qualità dei risultati binari 0 e 1. Se gli output non sono binari ma sono numeri fluttuanti tra 0 e 1, allora posso usarli come punteggi per la classificazione. Ma i numeri fluttuanti tra 0 e 1 urlano probabilità, e come faccio a sapere se posso fidarmi di loro come probabilità?

L’output di un modello può essere visto come una dichiarazione che dice quanto è probabile che qualcosa accada. Un esempio di tale modello – di cui controllo le dichiarazioni ogni giorno prima di uscire di casa – è il servizio meteorologico. In particolare, quanto è probabile che piova?

immagine da weather.com

Dice che domenica c’è un 80% di probabilità di pioggia. Quanto è affidabile questa chiamata all’80%? Se scavo nelle previsioni passate di weather.com e scopro che 8 giorni su 10 sono piovosi quando chiamano un 80%, allora posso convincermi a caricare i miei audiolibri e prepararmi per un traffico pazzesco sull’autostrada nel pomeriggio.

In altre parole, una previsione meteo accurata significa che se ho guardato in 100 giorni che sono previsti con un 80% di possibilità di pioggia, allora ci dovrebbero essere circa 80 giorni di pioggia. Deve anche essere accurata in altri intervalli di probabilità. Per i giorni che sono chiamati a piovere il 30% delle volte, ci dovrebbero essere 30 giorni di pioggia su 100 giorni in media. Se le previsioni di questo servizio di previsioni meteorologiche seguono tutte questo buon modello, allora diciamo che le loro previsioni sono calibrate. È il modo probabilistico di dire che hanno fatto centro.

• Un modello probabilistico è calibrato se ho suddiviso i campioni di test in base alle loro probabilità previste, i veri risultati di ogni bin hanno una proporzione vicina alle probabilità nel bin.

Come si valuta la calibrazione? Invece di riassumere la calibrazione in un singolo numero, preferisco fare dei grafici di calibrazione.

I grafici di calibrazione sono spesso grafici a linee. Una volta che ho scelto il numero di bin e gettato le previsioni nel bin, ogni bin viene poi convertito in un punto sul grafico. Per ogni bin, il valore y è la proporzione di risultati veri, e il valore x è la probabilità media prevista. Pertanto, un modello ben calibrato ha una curva di calibrazione che abbraccia la linea retta y=x. Ecco un esempio di un grafico di calibrazione con due curve, ognuna delle quali rappresenta un modello sugli stessi dati.

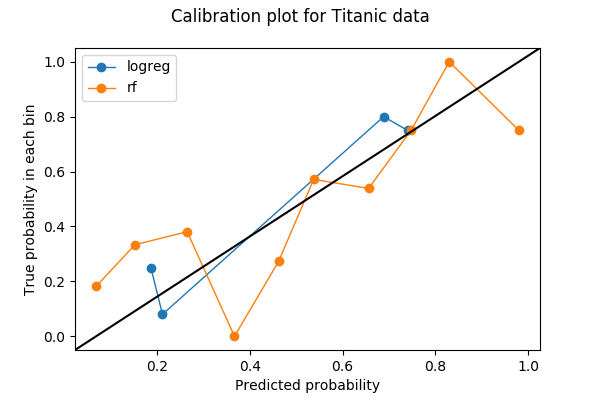
Vi mostro come ho fatto questo grafico in Python e cosa ho visto in esso.

Un esempio Python

La prima cosa da fare nel fare un plot di calibrazione è scegliere il numero di bins. In questo esempio, ho suddiviso le probabilità in 10 bins tra 0 e 1: da 0 a 0.1, da 0.1 a 0.2, …, da 0.9 a 1. I dati che ho usato sono il dataset Titanic da Kaggle, dove l’etichetta da predire è una variabile binaria Survived.

Segnalo le curve di calibrazione per due modelli – uno di regressione logistica e uno di foresta casuale. Entrambi i modelli producono probabilità di classe su Survived basate su due caratteristiche Age e Sex.

+----+------+--------+| Age| Sex|Survived|+----+------+--------+|22.0| male| 0||38.0|female| 1||26.0|female| 1|+----+------+--------+

Preprocessing

Prima di allenare i miei modelli, ho riempito i valori mancanti in Age con la sua media e ho anche trasformato Sex in una variabile numerica con valori 0 e 1.

import numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom sklearn import preprocessingfrom sklearn import model_selectiontitanic = pd.read_csv('train.csv')fitted_age_imputer = preprocessing.Imputer(axis=1).fit(titanic.values)titanic = fitted_age_imputer.transform( titanic.values.reshape(1, -1) ).transpose()titanic = np.where(titanic.Sex == 'female', 1, 0)

Poi, ho diviso i dati in training e validation set con una divisione 80/20.

from sklearn import model_selectionfeature_cols = feature_train, feature_test, label_train, label_test = ( model_selection.train_test_split( titanic, titanic.Survived, test_size=0.2, random_state=1) )

Allenamento e previsione

Posso ora allenare un modello di regressione logistica sul mio set di allenamento e prevedere sul set di validazione.

from sklearn.linear_model import LogisticRegressionlogreg_model = LogisticRegression().fit(X=feature_train,y=label_train)logreg_prediction = logreg_model.predict_proba(feature_test)

Similmente, addestrare un modello di foresta casuale e predire sul set di validazione.

from sklearn.ensemble import RandomForestClassifierrf_model = RandomForestClassifier(random_state=1234).fit(X=feature_train, y=label_train)rf_prediction = rf_model.predict_proba(feature_test)

La probabilità di classe positiva è restituita dai modelli nella seconda colonna (indice=1):

logreg_prediction

array(, , , , ])

Piano di calibrazione

Una volta che ho le probabilità di classe e le etichette, posso calcolare i bins per un grafico di calibrazione. Qui uso sklearn.calibration.calibration_curve che restituisce le (x,y) coordinate dei bins sul plot di calibrazione.

from sklearn.calibration import calibration_curvelogreg_y, logreg_x = calibration_curve(label_test, logreg_prediction, n_bins=10)

Nota che sebbene abbia chiesto 10 bins per la regressione logistica, 6 bins su 10 non hanno dati. La ragione è una combinazione del fatto che la regressione logistica è un modello semplice, che ci sono solo due caratteristiche, e che ho meno di 200 punti di dati nel set di validazione.

), array()]

In seguito, calcolo le coordinate per i bins del modello random forest.

rf_y, rf_x = calibration_curve(label_test, rf_prediction, n_bins=10)

Ora posso tracciare le due curve di calibrazione. Per rendere la trama più facile da leggere, ho anche aggiunto una linea di riferimento y=x basata su una risposta di StackOverflow.

%matplotlib inlineimport matplotlib.pyplot as pltimport matplotlib.lines as mlinesimport matplotlib.transforms as mtransformsfig, ax = plt.subplots()# only these two lines are calibration curvesplt.plot(logreg_x,logreg_y, marker='o', linewidth=1, label='logreg')plt.plot(rf_x, rf_y, marker='o', linewidth=1, label='rf')# reference line, legends, and axis labelsline = mlines.Line2D(, , color='black')transform = ax.transAxesline.set_transform(transform)ax.add_line(line)fig.suptitle('Calibration plot for Titanic data')ax.set_xlabel('Predicted probability')ax.set_ylabel('True probability in each bin')plt.legend()plt.show()

Somma dei bin e discriminazione

Ci sono solo 4 bin non vuoti per la regressione logistica quando ho chiesto 10 bin. È una cosa negativa? Usiamo una funzione che ho preso dal codice sorgente di sklearn.calibration.calibration_curve per scoprire quali sono i bin mancanti.

def bin_total(y_true, y_prob, n_bins): bins = np.linspace(0., 1. + 1e-8, n_bins + 1) # In sklearn.calibration.calibration_curve, # the last value in the array is always 0. binids = np.digitize(y_prob, bins) - 1 return np.bincount(binids, minlength=len(bins))bin_total(label_test, logreg_prediction, n_bins=10)

array(, dtype=int64)

I bidoni mancanti hanno valori medi del 5%, 35%, 45%, 55%, 85% e 95%. In effetti, avere dei totali bassi o dei bidoni vuoti nei bidoni medi (30-60%) può essere effettivamente una buona cosa – voglio che le mie previsioni evitino quei bidoni medi e diventino discriminanti.

La discriminazione è un concetto che va di pari passo con la calibrazione nei problemi di classificazione. A volte viene prima della calibrazione se l’obiettivo nella costruzione di un modello è quello di prendere decisioni automatiche piuttosto che fornire stime statistiche. Immaginate lo scenario in cui ho due modelli meteorologici e vivo a Podunk, Nevada, dove il 10% (36 giorni all’anno) dei giorni sono piovosi:

• il modello A dice sempre che c’è il 10% di possibilità di pioggia, non importa quale giorno sia.
• il modello B dice che pioverà ogni giorno in giugno (100%), e non piove mai negli altri 11 mesi (0%).

Il modello A è perfettamente calibrato. C’è solo un recipiente – il recipiente del 10% – e la vera probabilità è del 10%. Il modello B, invece, è leggermente fuori calibrazione perché ci saranno 30 giorni nel bin 100%, ma anche 6 giorni di pioggia nel bin 0%. Ma il modello B è chiaramente più utile se sto facendo programmi di escursioni nel fine settimana. Il modello B è più discriminante di A, perché è più facile prendere decisioni (escursioni/non escursioni) sulla base dei risultati del modello B.

La discriminazione è spesso controllata con le curve caratteristiche operative del ricevitore, o curve ROC, ma questo è un argomento per un altro post.

Cross-validation?

Se non mi interessa la discriminazione e voglio solo una buona calibrazione, allora la regressione logistica (blu) sembra fare meglio della foresta casuale (arancione). È davvero così? In particolare, se guardo il numero di punti nei bins per la foresta casuale,

bin_total(label_test, rf_prediction, n_bins=10)

array(, dtype=int64)

Sospetto che il problema possa essere che alcuni bins hanno troppo pochi punti dati. Ho messo 200 punti in 10 bins, quindi alcuni bins ne avranno solo alcuni, quindi il plot di calibrazione soffre perché un errore di classificazione in un piccolo bin cambia notevolmente la proporzione.

Solo il 20% dei miei dati è stato usato nel plot precedente, quindi forse posso usarne di più. Per utilizzare tutti i miei dati nel testare la calibrazione tra diversi modelli, ho pensato che posso rubare l’idea della convalida incrociata. Se divido i miei dati in 5 pieghe per la convalida incrociata, allora ogni piega sarà usata una volta come set di convalida. Pertanto, posso concatenare le probabilità previste da tutte e 5 le pieghe e farne un grafico di calibrazione. Il risultato di una trama di calibrazione a 5 pieghe è la seguente trama. Il codice può essere trovato nell’ultima sezione del quaderno Jupyter.

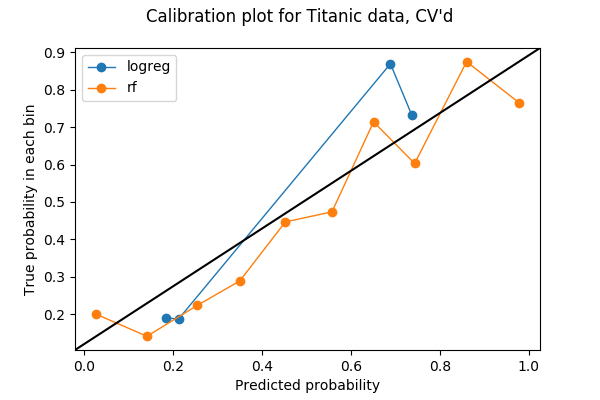
Ora ogni bin ha più punti:

array(, dtype=int64)

e penso si possa dire che, in questo esempio, la foresta casuale è meglio calibrata della regressione logistica.

***

Nate Silver ha un grande esempio sulla calibrazione del tempo nel libro The Signal and the Noise, dove ha studiato le previsioni di tre fonti – il National Weather Service, il Weather Channel e i canali di notizie locali – nel capitolo 4, For Years You’ve Been Telling Us That Rain Is Green. Ha concluso che la maggior parte dei canali di notizie locali sono mal calibrati e sono “bagnati”. È una gemma, e vi consiglio di prendere il libro se riuscite a metterci le mani sopra.

Ho imparato per la prima volta la calibrazione attraverso il mio collega Kevin nel 2016 quando abbiamo discusso diverse metriche sui modelli di classificazione. Senza di lui, probabilmente mi ci vorranno un altro anno o due prima di capire l’importanza della calibrazione, e molto più tardi prima di scrivere questo post.