Cristallografia. Diffusione e diffrazione. La legge di Bragg

Se, dopo la riflessione, le onde emergenti sono in fase, l’intensità riflessa sarà osservata, cioè, la legge di Bragg è soddisfatta.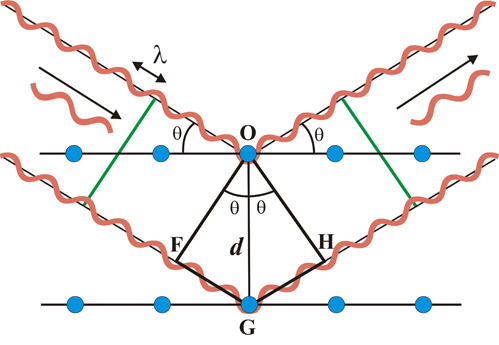
Come è stato dimostrato con le equazioni di Laue, la legge di Bragg proposta da entrambi, padre e figlio (WilliamH. Bragg e WilliamL. Bragg), può anche essere derivata graficamente in modo semplice…
L’ipotesi è di immaginare la diffrazione di Bragg come una riflessione dei raggi X sulla superficie di “specchi” immaginari formati da piani atomici nell’attico cristallino (mostrati come linee orizzontali contenenti centri di diffusione, cioè gli atomi mostrati come cerchi blu nell’immagine di sinistra). A causa della natura ripetitiva del cristallo, questi piani sarebbero separati da una distanza costante d.
I due raggi X di lunghezza d’onda λ, arrivano in fase sui rispettivi piani immaginari, con un angolo di incidenza θ, e formano un fronte d’onda (linea verde a sinistra).er ottenere un effetto cooperativo, dopo la riflessione i due fasci di raggi X devono essere ancora in fase (linea verde a destra), situazione che si verifica solo se la differenza di percorso dei fronti d’onda OF e OH (fronti d’onda prima e dopo la riflessione) corrisponde a un numero intero di lunghezze d’onda.
Questa condizione è equivalente a dire che la somma dei segmenti FGe GH corrisponde a un numero intero (n) per la lunghezza d’onda (λ):

Questa è la Legge di Bragg.

Se le onde riflesse emergenti hanno fase opposta, non si osserva alcuna intensità riflessa, cioè, la Legge di Bragg non è soddisfatta.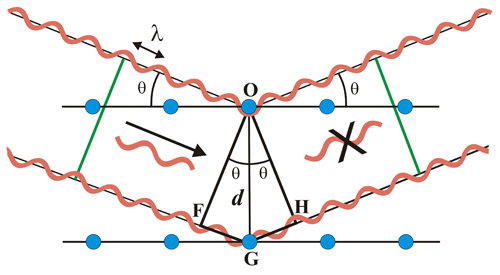
Quando l’angolo di incidenza dei raggi X non soddisfa la Legge di Bragg, i fasci emergenti non sono più in fase (linea verde sulla destra), e si annullano a vicenda, cosicché non si osserva alcuna intensità riflessa.
Se consideriamo lo scenario di base e guardiamo attentamente la legge di Bragg, è facile realizzare che: