Equazioni di instabilità delle colonne
Nell’ultimo post di questa serie, abbiamo introdotto alcuni concetti fondamentali usando una struttura semplificata idealizzata. In questo post inizieremo a considerare strutture più realistiche e a determinare le equazioni di instabilità delle colonne. In particolare, determineremo un’espressione per un carico critico per una colonna caricata assialmente con estremità bloccate. Poi esploreremo alcune altre condizioni di supporto.
📓 Questo post è la seconda parte di una serie in tre parti sull’instabilità delle colonne. Puoi scaricare gratuitamente la serie completa in tre parti, ben formattata e impaginata in un ebook.
Copriremo un bel po’ di cose in questo, quindi ecco l’indice…
- Colonne bloccate alle due estremità
- Stabilire l’equazione differenziale
- Solvere l’equazione differenziale
- Risolvere le costanti di integrazione
- Modi di imbarcamento e forme dei modi
- Flessione massima sotto carico critico
- Modi di imbarcamento di ordine superiore
- Colonne con altre condizioni di supporto
- Fisso-Fisso
- Fisso-Libero
- Fisso-Appuntato
- Asse di instabilità
- Sollecitazione critica
- Lunghezza effettiva della colonna
Quando ci riferiamo ad un supporto a perno, si tratta di un supporto che non offre alcuna resistenza alla rotazione. A volte ci imbattiamo nella pratica in supporti a perno che si avvicinano molto a questa definizione teorica. Ecco alcuni esempi:
Ai fini della nostra discussione qui, daremo per scontato che abbiamo a che fare con supporti a perno come questi, e che non inibiscono la rotazione della struttura.
1.0 Equazione di instabilità per colonne bloccate alle due estremità
Per analizzare questa struttura, useremo l’equazione differenziale della curva di deformazione in cui ![]() è il momento flettente interno ad una data sezione,
è il momento flettente interno ad una data sezione, ![]() rappresenta la deflessione laterale della colonna e
rappresenta la deflessione laterale della colonna e ![]() la distanza sulla lunghezza della colonna.
la distanza sulla lunghezza della colonna. ![]() si riferisce alla rigidità flessionale ed è il prodotto del modulo di Young
si riferisce alla rigidità flessionale ed è il prodotto del modulo di Young ![]() e il secondo momento dell’area della sezione
e il secondo momento dell’area della sezione ![]() .
.
![]()
💡 Questa equazione modella semplicemente la forma deflessa della colonna per una data rigidità flessionale.
È probabile che tu abbia incontrato questa equazione altrove nei tuoi studi di ingegneria. La nostra colonna deflessa lateralmente si comporta più o meno come una trave. Ricordate che l’instabilità è un cedimento per flessione piuttosto che un cedimento dovuto alla compressione diretta (schiacciamento). Il nostro compito ora è quello di utilizzare questa equazione per ricavare un’espressione per il carico assiale critico in una colonna con estremità a perno.
📌 Proprio come per la struttura idealizzata discussa nel post precedente, anche qui la nostra derivazione assumerà che tutte le deformazioni siano piccole rispetto alle dimensioni della struttura.
Stabiliamo l’equazione differenziale
Prima consideriamo la struttura, la sua forma deflessa e il diagramma a corpo liberocorpo libero che risulta dal taglio della struttura ad una distanza ![]() dal supporto inferiore…
dal supporto inferiore…
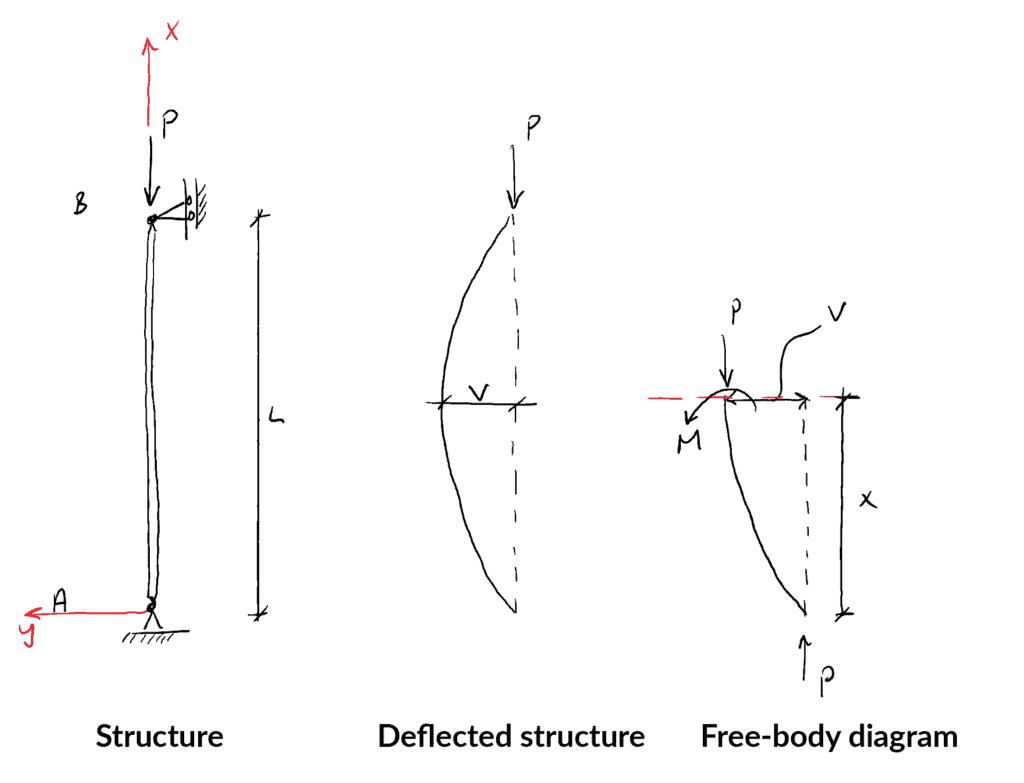
Prendendo i momenti intorno al punto A si ottiene:
![]()
Sostituendo ![]() nell’equazione differenziale della curva di flessione e riorganizzando leggermente si ottiene:
nell’equazione differenziale della curva di flessione e riorganizzando leggermente si ottiene:
![]()
Questa è un’equazione differenziale lineare, omogenea, del 2° ordine con coefficienti costanti. È anche un’equazione che modella la forma deflessa della nostra struttura e contiene ![]() , il carico assiale. Seguendo lo stesso approccio della struttura idealizzata discussa in precedenza, se risolviamo questa equazione possiamo determinare
, il carico assiale. Seguendo lo stesso approccio della struttura idealizzata discussa in precedenza, se risolviamo questa equazione possiamo determinare ![]() , il valore del carico applicato al quale è bilanciato dalla resistenza alla flessione della colonna.
, il valore del carico applicato al quale è bilanciato dalla resistenza alla flessione della colonna.
Siamo quindi di fronte al tentativo di risolvere un’equazione differenziale. A questo punto, è utile poter indicare la soluzione generale di questa forma di equazione differenziale:
![]()
Risolvere l’equazione differenziale
Se vuoi fare una deviazione a questo punto per vedere come si risolve l’equazione differenziale, guarda il video qui sotto. Altrimenti, continueremo a lavorare sulle costanti di integrazione nella prossima sezione.
Risolvere le costanti di integrazione
Ora che abbiamo la soluzione generale per questo formato di equazione, dobbiamo risolvere le costanti di integrazione usando le condizioni al contorno (pinned-pinned) per la nostra colonna.
Condizione limite 1:
A ![]() (base della colonna al supporto del perno),
(base della colonna al supporto del perno), ![]() (la flessione laterale deve essere uguale a zero. Imponendo queste condizioni alla nostra soluzione generale si ottiene:
(la flessione laterale deve essere uguale a zero. Imponendo queste condizioni alla nostra soluzione generale si ottiene:
![]()
Quindi
![]()
Come risultato la nostra soluzione si riduce a:
![]()
Condizione limite 2:
A ![]() (cima della colonna al supporto del perno),
(cima della colonna al supporto del perno), ![]() (anche la deflessione laterale è nulla). Di nuovo, imponendo queste condizioni al contorno si ottiene,
(anche la deflessione laterale è nulla). Di nuovo, imponendo queste condizioni al contorno si ottiene,
![]()
Quindi, o ![]() è uguale a zero o
è uguale a zero o ![]() è uguale a zero. Se
è uguale a zero. Se ![]() è uguale a zero, l’equazione è soddisfatta per qualsiasi valore di
è uguale a zero, l’equazione è soddisfatta per qualsiasi valore di ![]() . Questo non ci fa andare avanti… possiamo pensare a questa soluzione come alla soluzione banale. Più interessante è il caso in cui:
. Questo non ci fa andare avanti… possiamo pensare a questa soluzione come alla soluzione banale. Più interessante è il caso in cui:
![]()
Conoscendo quello che sappiamo sulle ![]() , questa equazione può essere vera solo quando,
, questa equazione può essere vera solo quando,
![]()
Possiamo scartare il caso in cui,
![]()
In questo scenario, ![]() dovrebbe essere uguale a zero (poiché tutti gli altri termini hanno valori non nulli per definizione) e sappiamo che questo non è il caso. Quindi, per una colonna appuntata, la nostra soluzione è:
dovrebbe essere uguale a zero (poiché tutti gli altri termini hanno valori non nulli per definizione) e sappiamo che questo non è il caso. Quindi, per una colonna appuntata, la nostra soluzione è:
![]()
dove ![]() … Infine, possiamo riorganizzare questa equazione per rendere
… Infine, possiamo riorganizzare questa equazione per rendere ![]() il soggetto dell’equazione:
il soggetto dell’equazione:
![]()
Per ![]() …
…
📌 Questa equazione rappresenta una serie infinita di carichi di instabilità. Il più basso ![]() è il carico critico di instabilità, noto anche come carico di Eulero
è il carico critico di instabilità, noto anche come carico di Eulero ![]() .
.
![]()
2.0 Modalità di instabilità e forme dei modi
Finora, abbiamo stabilito che esiste una serie infinita di carichi di instabilità e il più basso è quello critico e chiamato carico di instabilità di Eulero. Questo solleva la domanda: a cosa corrispondono i carichi di instabilità più grandi?
Questi sono i carichi che corrispondono ai modi di instabilità superiori. Ogni modo di instabilità ha una forma corrispondente. Per esplorare ulteriormente questo, ritorniamo alla nostra soluzione generale dopo aver stabilito che ![]() :
:
![]()
L’applicazione della nostra seconda condizione limite ci ha portato a stabilire la relazione
![]()
Combinando queste due equazioni si ottiene:
![]()
per ![]() … Questa equazione descrive la forma deflessa della colonna per ogni valore del carico di instabilità
… Questa equazione descrive la forma deflessa della colonna per ogni valore del carico di instabilità ![]() definito sopra. Solo quando il carico assiale ha uno dei valori dati dall’equazione (precedentemente definita)…
definito sopra. Solo quando il carico assiale ha uno dei valori dati dall’equazione (precedentemente definita)…
![]()
…la colonna può avere una forma piegata ed essere in equilibrio. Per qualsiasi altro carico, la colonna sarebbe dritta e in uno stato di equilibrio STABILE ![]() o di equilibrio INSTABILE
o di equilibrio INSTABILE ![]() . Ricordiamo questo concetto dalla nostra precedente discussione sulle strutture di colonne idealizzate nell’ultimo post:
. Ricordiamo questo concetto dalla nostra precedente discussione sulle strutture di colonne idealizzate nell’ultimo post:
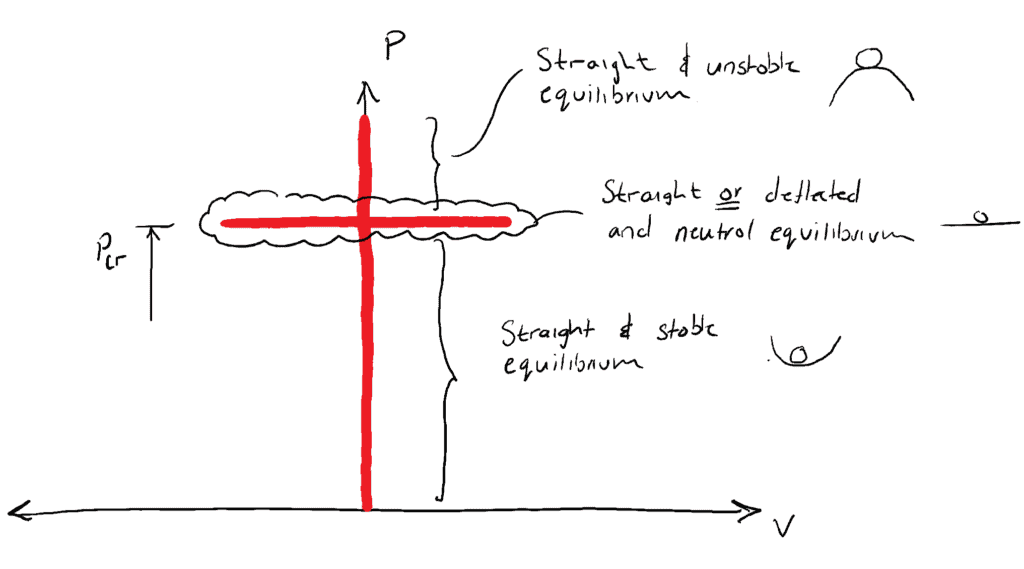
Deformazione massima sotto carico critico
La nostra equazione per la forma deformata o instabile di una colonna contiene il parametro ![]() , rimasto dalla nostra soluzione generale dell’equazione differenziale. Riconosciamo ora che
, rimasto dalla nostra soluzione generale dell’equazione differenziale. Riconosciamo ora che ![]() rappresenta la grandezza dell’onda sinusoidale o, in questo contesto, la massima deflessione laterale per la deviazione/incurvatura (definita sopra):
rappresenta la grandezza dell’onda sinusoidale o, in questo contesto, la massima deflessione laterale per la deviazione/incurvatura (definita sopra):
![]()
Se ora ricordiamo gli stati di equilibrio, quando la colonna è nella sua forma inarcata ![]() e in uno stato di equilibrio neutro, la deflessione laterale massima può avere qualsiasi valore che soddisfa ancora la nostra ipotesi di piccola deflessione. Possiamo rappresentare il valore di
e in uno stato di equilibrio neutro, la deflessione laterale massima può avere qualsiasi valore che soddisfa ancora la nostra ipotesi di piccola deflessione. Possiamo rappresentare il valore di ![]() graficamente…
graficamente…
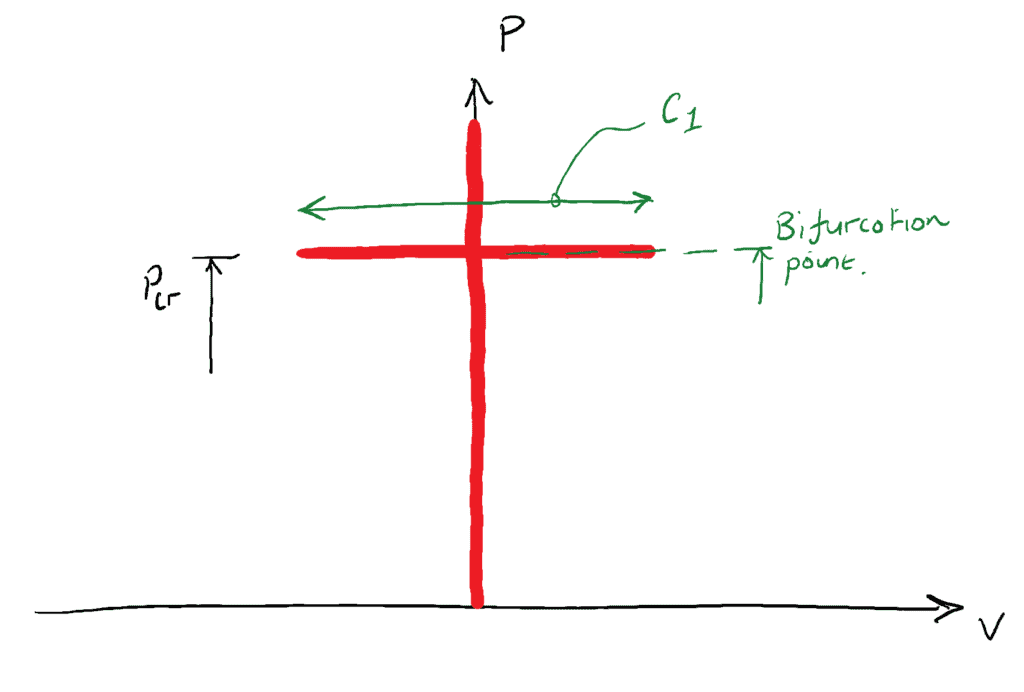
Il valore di ![]() è quindi matematicamente indefinito, può avere qualsiasi valore “piccolo”. Fortunatamente questo non ci causa alcuna difficoltà pratica, come detto in precedenza, lo stato di equilibrio neutro non è qualcosa che osserviamo nella pratica dell’ingegneria civile. A tutti gli effetti, per un ingegnere civile o strutturale, una colonna che sperimenta
è quindi matematicamente indefinito, può avere qualsiasi valore “piccolo”. Fortunatamente questo non ci causa alcuna difficoltà pratica, come detto in precedenza, lo stato di equilibrio neutro non è qualcosa che osserviamo nella pratica dell’ingegneria civile. A tutti gli effetti, per un ingegnere civile o strutturale, una colonna che sperimenta ![]() è considerata fallita. Questo stato teorico di equilibrio neutro è noto anche come punto di biforcazione.
è considerata fallita. Questo stato teorico di equilibrio neutro è noto anche come punto di biforcazione.
Modi di instabilità di ordine superiore
Immaginate una colonna con estremità a perno caricata assialmente che è trattenuta lateralmente nel suo punto di media altezza (per esempio da una soletta). La colonna sarebbe impedita dall’instabilità sotto il primo carico critico (instabilità di Eulero) a causa del vincolo laterale. Il vincolo della soletta tiene letteralmente la colonna e le impedisce di deformarsi.
Come risultato di questo vincolo, la colonna può portare più carico, fino a raggiungere il secondo carico di instabilità ![]() . Poiché la colonna non è trattenuta contro l’instabilità nel secondo modo, ora si instabilizzerebbe (o teoricamente entrerebbe in uno stato di equilibrio neutro).
. Poiché la colonna non è trattenuta contro l’instabilità nel secondo modo, ora si instabilizzerebbe (o teoricamente entrerebbe in uno stato di equilibrio neutro).
💡 Un adeguato vincolo laterale aumenta la resistenza di una colonna all’instabilità “chiudendo” la possibilità di instabilità nei modi inferiori e “sbloccando” i carichi di instabilità più alti.
Possiamo facilmente visualizzare i primi tre modi di instabilità semplicemente valutando le equazioni del carico e della forma deviata per ![]() .
.
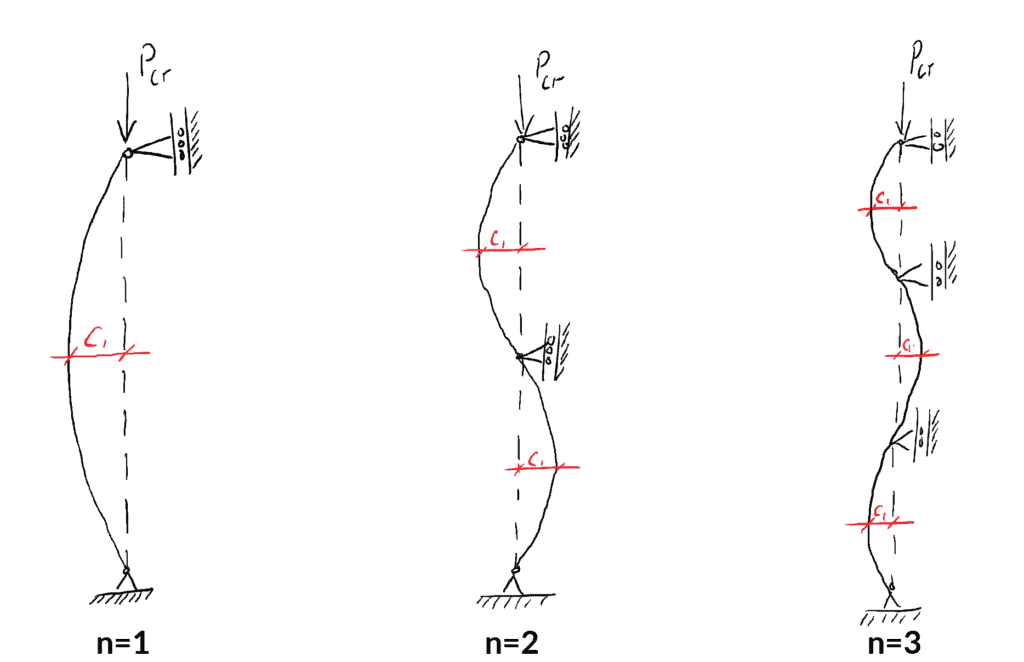
Modo
![]()
![]()
Critical Load
![]()
![]()
![]()
Forma ad incastro
![]()
![]()
![]()
📌 Per qualsiasi modalità data, ![]() rappresenta il limite superiore pratico del carico assiale. Le imperfezioni naturali, per esempio la colonna ‘fuori piombo’ o il cattivo allineamento del carico indurranno quasi certamente l’instabilità quando il carico critico viene superato.
rappresenta il limite superiore pratico del carico assiale. Le imperfezioni naturali, per esempio la colonna ‘fuori piombo’ o il cattivo allineamento del carico indurranno quasi certamente l’instabilità quando il carico critico viene superato.
3.0 Colonne con altre condizioni di supporto
Finora abbiamo guardato il comportamento di una colonna bloccata ad entrambe le estremità. Questo è il tipico punto di partenza. Ma lo stesso processo può essere seguito per determinare le equazioni corrispondenti per colonne con diversi tipi di condizioni di supporto. Nei video qui sotto, eseguirò le derivazioni per dimostrare il processo per:
- Colonne con una base fissata contro la rotazione e libera in cima (fixed-free)
- Colonne fissate contro la rotazione ad entrambe le estremità (fixed-fixed)
- Colonne fissate contro la rotazione alla base e bloccate in cima (fixed-appuntato)
Equazione di bloccaggio per colonne trattenute contro la rotazione ad entrambe le estremità (fisso-fisso)
Equazione di bloccaggio per colonne trattenute contro la rotazione alla base e libere in cima (fisso-libero)
Equazione deluckling per colonne trattenute contro la rotazione in basso e bloccate in alto (fisso-appuntato)
Riassunto delle condizioni di supporto
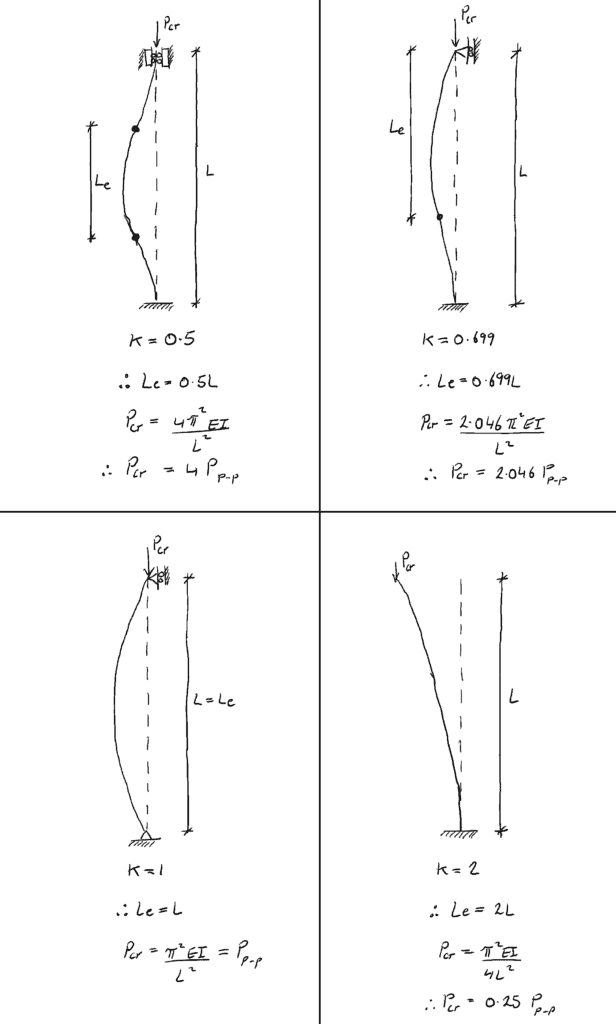
4.0 Asse di imbarcamento
Ricordiamo dall’equazione per il carico di instabilità che è una funzione di I, il secondo momento dell’area della sezione trasversale:
![]()
Quindi per una data sezione trasversale, una colonna si deformerà sempre intorno all’asse con il secondo momento d’area più basso, l’asse ‘debole’. Questo presuppone che entrambi gli assi abbiano lo stesso vincolo. Consideriamo il caso di una sezione di colonna universale (UC) sotto compressione:
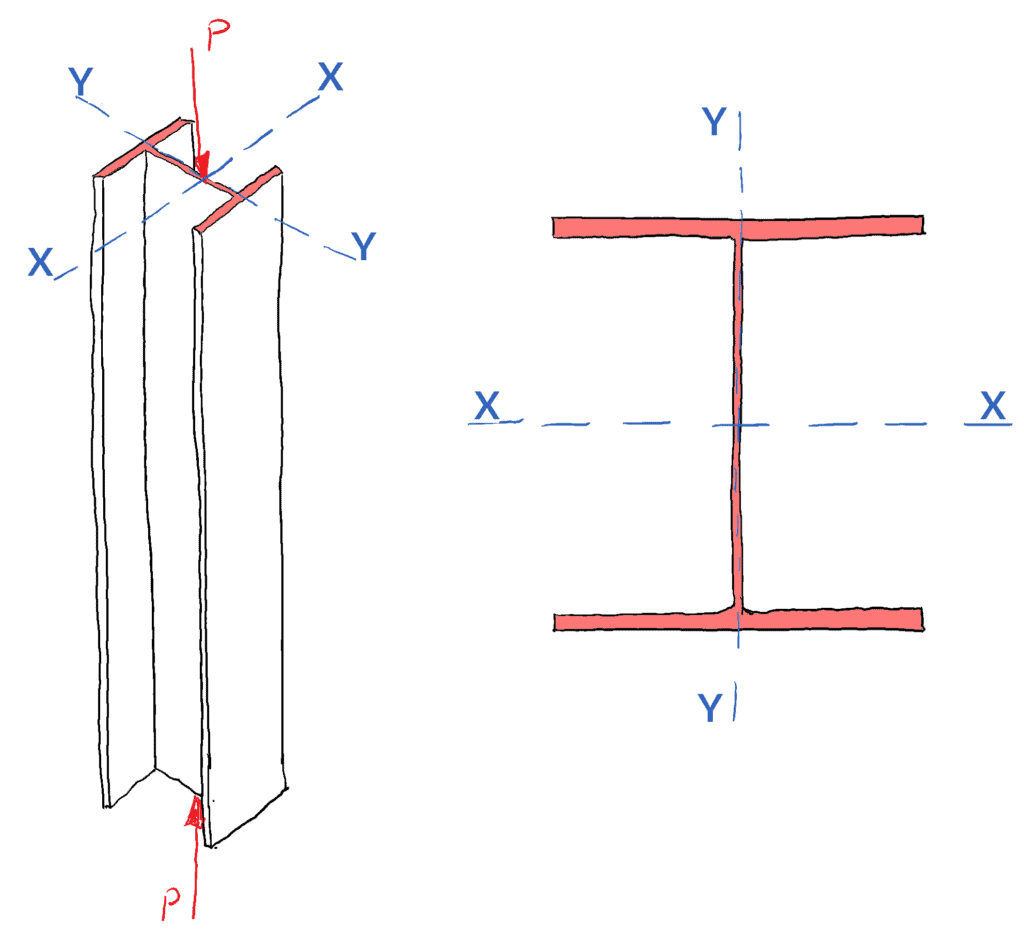
Siccome l’asse X-X, è l’asse del principio maggiore (con il più grande valore del secondo momento dell’area – potresti ricordarlo dal tuo studio del cerchio di Mohr), è l’asse più forte e quindi la colonna si piegherà prima intorno al principio minore o all’asse Y-Y.
Quando si considera il carico di instabilità per una struttura a colonna, la forma della sezione trasversale gioca un ruolo chiave, si dovrebbero valutare gli assi principali maggiori e minori per determinare l’asse critico per l’instabilità.
5.0 Sollecitazione critica
📌 La sollecitazione critica è la sollecitazione assiale media in una sezionesezione sotto il carico critico
![]()
Definiremo ora il Raggio di Giro come:
![]()
Possiamo quindi scrivere lo stress critico come:
![]()
Finalmente definiamo il rapporto di snellezza come:
![]()
Il rapporto di snellezza è una misura molto utile della geometria di una colonna e della sua suscettibilità alla deformazione. Un alto rapporto di snellezza indica una maggiore suscettibilità all’instabilità. Il rapporto di snellezza deve essere determinato separatamente per ogni asse principale. Possiamo avere un’intuizione del rapporto di snellezza visualizzando entrambi gli estremi,
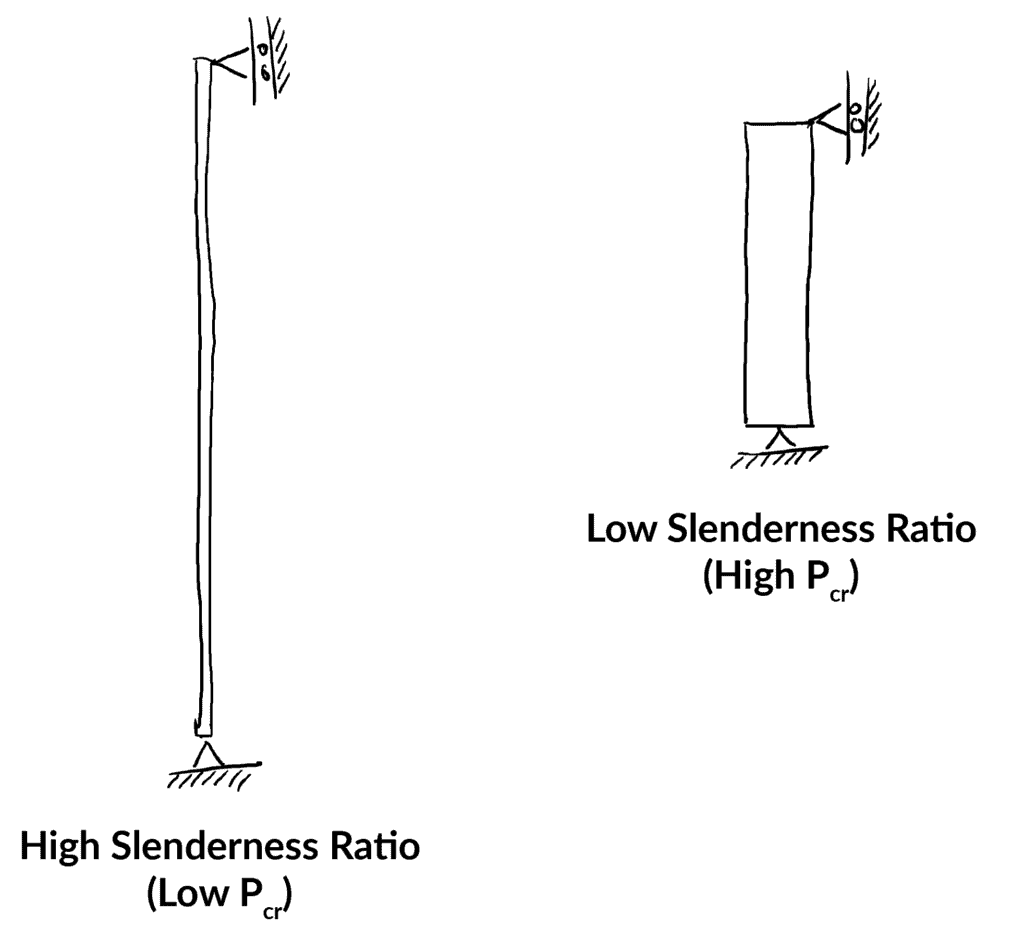
L’equazione dello sforzo critico può quindi essere scritta in funzione del rapporto di snellezza come segue,
![]()
Tracciando la tensione critica in funzione del rapporto di snellezza per un dato valore del modulo di Young si ottiene una curva di Eulero che mostra l’intervallo di sicurezza della sollecitazione assiale media per un dato rapporto di snellezza (o l’intervallo di sicurezza dei valori del rapporto di snellezza per una data sollecitazione assiale),
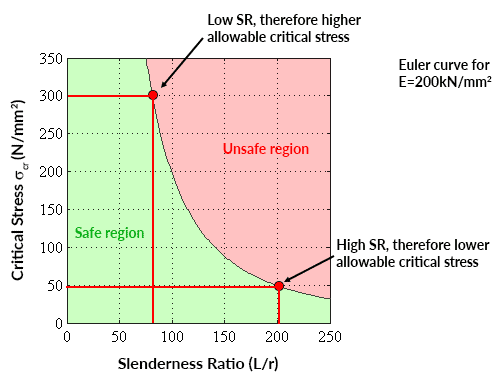
📌 Una curva di Eulero è valida solo per sollecitazioni critiche inferiori allo snervamento del materiale
6.0 Lunghezza effettiva della colonna
L’ultimo concetto che esamineremo in questo post è la lunghezza effettiva della colonna. La lunghezza effettiva di una colonna, ![]() , è la lunghezza tra i punti di flessione sulla curva/forma deviata (anche se la forma deve essere estesa fino a raggiungere un punto di flessione – discusso di seguito). Per una colonna bloccata ad entrambe le estremità, la lunghezza effettiva è semplicemente l’intera lunghezza della colonna tra i vincoli dei perni:
, è la lunghezza tra i punti di flessione sulla curva/forma deviata (anche se la forma deve essere estesa fino a raggiungere un punto di flessione – discusso di seguito). Per una colonna bloccata ad entrambe le estremità, la lunghezza effettiva è semplicemente l’intera lunghezza della colonna tra i vincoli dei perni:
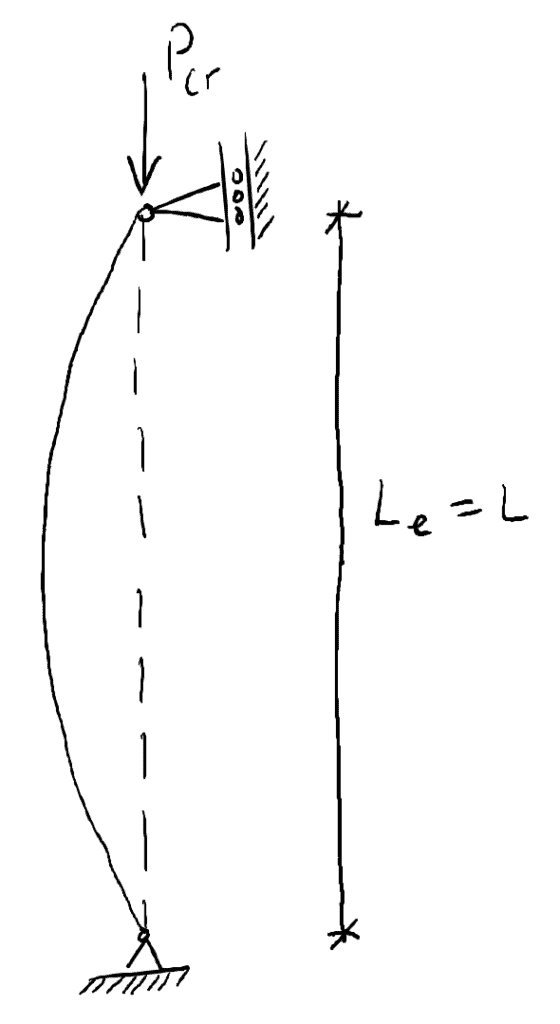
Considera una colonna con un supporto fisso alla base e nessun vincolo laterale in cima (senza vincoli). Alla base, nessuna rotazione può avvenire. Per ottenere due punti di flessione sulla forma deflessa, essa deve essere estesa…
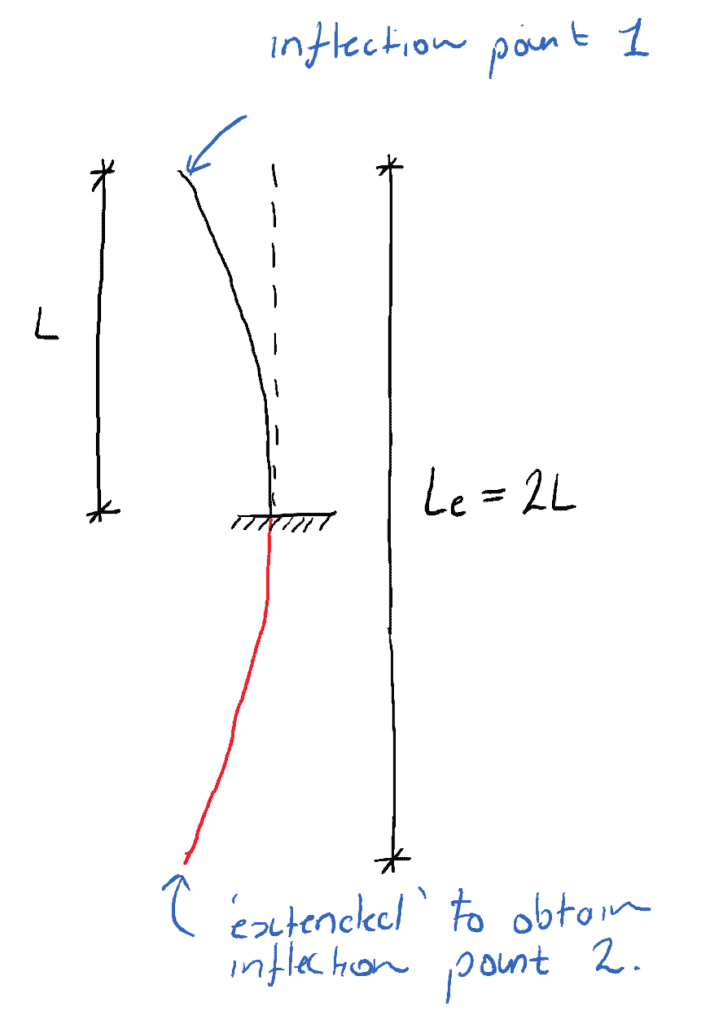
La porzione rossa ‘immaginaria’ della forma deflessa è l’estensione richiesta per fornire il punto di flessione numero 2. Quindi la lunghezza effettiva per una colonna senza punto fisso è 2L.
📌 Un altro modo di pensare alla lunghezza effettiva è che è la lunghezza di una colonna equivalente con estremità appuntate.
Prima di concludere la nostra discussione sulla lunghezza effettiva, possiamo definire un’espressione generale per il carico critico come:
![]()
Se ora introduciamo il fattore lunghezza efficace, ![]() , tale che
, tale che ![]() , possiamo indicare il carico critico in funzione del fattore di lunghezza efficace:
, possiamo indicare il carico critico in funzione del fattore di lunghezza efficace:
![]()
Abbonati agli aggiornamenti
Vieni avvisato quando arrivano nuovi tutorial e corsi



