Frazioni equivalenti

Le frazioni equivalenti hanno lo stesso valore, anche se possono sembrare diverse.

Queste frazioni sono davvero uguali:

12 = 24 = 48

Perché sono uguali? Perché quando moltiplichi o dividi sia la parte superiore che quella inferiore per lo stesso numero, la frazione mantiene il suo valore.

La regola da ricordare è:

“Cambia la parte inferiore usando moltiplica o dividi,
E lo stesso deve essere applicato alla parte superiore”

Ecco perché queste frazioni sono davvero uguali:

	× 2		× 2
1	=	2	=	4
2		4		8
	× 2		× 2

E visivamente appare così:

1/2		2/4		4/8
	=		=

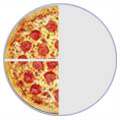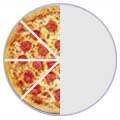Vedi Frazioni sulla linea dei numeri …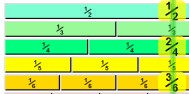

… mostra molte frazioni equivalenti.

Vedi anche il Grafico delle Frazioni con molti esempi di frazioni equivalenti.

Dividendo

Ecco altre frazioni equivalenti, questa volta dividendo:

	÷ 3		÷ 6
18	=	6	=	1
36		12		2
	÷ 3		÷ 6

Scegliete attentamente il numero per cui dividete, in modo che i risultati (sia in alto che in basso) rimangano numeri interi.

Se continuiamo a dividere finché non possiamo andare oltre, allora abbiamo semplificato la frazione (l’abbiamo resa il più semplice possibile).