Inversione della matrice: Trovare l’inverso di una matrice

Per le matrici, non esiste la divisione. Puoi aggiungere, sottrarre e moltiplicare matrici, ma non puoi dividerle. C’è un concetto correlato, però, che si chiama “inversione”. Prima discuterò perché l’inversione è utile, e poi vi mostrerò come farla.

Pensate a quando avete imparato per la prima volta come risolvere le equazioni lineari. Se ti fosse stato dato qualcosa come “3x = 6”, avresti risolto dividendo entrambi i lati per 3. Poiché moltiplicare per1/3 è lo stesso che dividere per 3, potresti anche moltiplicare entrambi i lati per 1/3 per ottenere la stessa risposta: x = 2. Se avevi bisogno di risolvere qualcosa come “(3/2)x = 6”, potresti ancora dividere entrambi i lati per 3/2, ma probabilmente era più facile moltiplicare entrambi i lati per 2/3. La frazione reciproca 2/3 è l’inverso di 3/2 perché, se si moltiplicano le due frazioni, si ottiene 1, che è, in questo contesto, chiamato “l’identità (moltiplicativa)”: 1 è chiamato identità perché moltiplicando qualcosa per 1 non cambia il suo valore.

Questa terminologia e questi fatti sono molto importanti per le matrici. Se vi viene data un’equazione di matrice come AX = C, dove vi vengono dati A e C e vi viene detto di calcolare X, vorreste “dividere” la matrice A. Ma non si può fare la divisione con le matrici. D’altra parte, e se si potesse trovare l’inverso di A, qualcosa di simile al trovare la frazione reciproca di cui sopra? L’inverso di A, scritto come “A-1” e pronunciato “A inverso”, ti permetterebbe di cancellare A dall’equazione della matrice e poi risolvere X.

AX = C
A-1AX = A-1C
IX = A-1C
X = A-1C

Come ha fatto “A-1AX” sul lato sinistro dell’equazione a diventare “X”? Ripensate alla natura degli inversi per i numeri regolari. Se hai un numero (come 3/2) e il suo inverso (in questo caso, 2/3) e li moltiplichi, ottieni 1. E 1 è l’identità, così chiamata perché 1x = x per qualsiasi numero x. Funziona allo stesso modo per le matrici. Se si moltiplica una matrice (come A) e la sua inversa (in questo caso,
A-1), si ottiene la matrice identità I. E il punto della matrice identità è che IX = X per qualsiasi matrice X (intendendo “qualsiasi matrice della dimensione corretta”, ovviamente).

Si noti che l’ordine nella moltiplicazione di cui sopra è importante e non è affatto arbitrario. Ricordiamo che, per le matrici, la moltiplicazione non è commutativa. Cioè, AB non è quasi mai uguale a BA. Quindi moltiplicare l’equazione della matrice “a sinistra” (per ottenere A-1AX) non è affatto la stessa cosa che moltiplicare “a destra” (per ottenere AXA-1). E non puoi dire che il prodotto AXA-1 è uguale a A-1AX, perché non puoi cambiare l’ordine nella moltiplicazione. Invece, devi moltiplicare A-1 a sinistra, mettendolo proprio accanto alla A nell’equazione originale della matrice. E poiché devi fare la stessa cosa ad entrambi i lati di un’equazione quando risolvi, devi moltiplicare “a sinistra” anche sul lato destro dell’equazione, ottenendo A-1C. Non puoi essere casuale con il posizionamento delle matrici; devi essere preciso, corretto e coerente. Questo è l’unico modo per cancellare con successo A e risolvere l’equazione della matrice.

Come avete visto sopra, le matrici inverse possono essere molto utili per risolvere le equazioni di matrice. Ma, data una matrice, come si fa ad invertirla? Come si trova l’inverso? La tecnica per invertire le matrici è piuttosto intelligente. Per una data matrice A e la sua inversa A-1, sappiamo che abbiamo A-1A = I. Useremo la matrice identità I nel processo di inversione di una matrice.

• Trova l’inversa della seguente matrice.

Prima, scrivo le voci della matrice A, ma le scrivo in una matrice doppia:

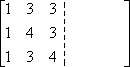
Nell’altra metà della doppia larghezza, scrivo la matrice identità:

Ora farò le operazioni di riga della matrice per convertire il lato sinistro della doppia larghezza nell’identità. (Come sempre con le operazioni di riga, non c’è un modo “giusto” per farlo. Quelli che seguono sono solo i passi che mi sono capitati. I vostri calcoli potrebbero facilmente essere molto diversi.)

Ora che il lato sinistro della doppia larghezza contiene l’identità, il lato destro contiene l’inverso. Cioè, la matrice inversa è la seguente:

Nota che possiamo confermare che questa matrice è l’inversa di A moltiplicando le due matrici e confermando che abbiamo l’identità: Copyright © Elizabeth Stapel 2003-2011 All Rights Reserved

Be advised that, in “real life”, the inverse is rarely a matrix filled with nice neat whole numbers like this. Con un po’ di fortuna, però, specialmente se state facendo le inverse a mano, ve ne verranno date di belle come questa da fare.

Top | 1 | 2 | Return to Index Next >>