Qual è il numero più grande?

I numeri vanno avanti all’infinito – ma sulla strada verso l’infinito, ci sono alcuni way post piuttosto remoti.

Per i nostri antenati, un milione era grande quanto i numeri dovevano diventare. Non c’era bisogno di invocare i miliardi (1.000.000.000) della finanza o i terabyte (1012) dell’informatica. La tecnologia ci ha reso blasé sull’uso di numeri di 9 o 12 cifre nelle conversazioni. Tuttavia, c’è ancora molta strada da fare prima di raggiungere la scala del nostro posto nell’universo, per non parlare dei numeri vertiginosamente giganteschi che i matematici hanno immaginato.

Numeri standard

Oltre il miliardo – l’ordine di grandezza della popolazione umana – dobbiamo davvero dire addio all’idea di avere nomi per i numeri. (Anche se esistono fino a 1063, non sono di uso comune). Per la distanza percorsa dalla luce in un minuto, il numero di atomi in un grammo di carbonio o la distanza tra le galassie, gli scienziati usano la forma standard per esprimersi. La forma standard registra tutti i numeri nel formato a × 10n, dove a è un numero tra 1 e 10 e n può essere qualsiasi numero. È quello che si usa per parlare del numero di atomi di carbonio in un campione di 12 g. Che, per inciso, è 6,22 × 1023, il numero di Avogadro, e abbastanza grande. L’universo osservabile è largo circa 8,8 × 1023 km, e ci sono circa 1087 particelle in esso. Ma più grandi di questi numeri sono i costrutti delle menti matematiche.

Lascia che ti faccia un googol

Immortalato nell’uso comune dal gigante di internet, un googol è il numero 10100 – 10, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000. Il matematico americano Edward Kasner chiese a suo nipote Milton di dargli un nome, e un googol divenne. Ma il prossimo numero veramente grande è il googolplex, che eleva 10 alla potenza di un googol. Questo è astronomicamente più grande di un googol – è impossibile scrivere un googolplex in notazione standard anche se si scrivesse una singola cifra su ogni particella dell’universo.

La potenza delle potenze

Aggiungere un esponenziale nell’esponente aumenta davvero il tasso di ingrandimento dei numeri.

3×3×3=27

3(33) = 7.625.597.484.987

Naturalmente, alla ricerca di numeri più grandi, si aggiungono sempre più potenze alla torre. Questo però diventa rapidamente scomodo da scrivere, oltre a portare a torri che fanno sembrare quella di Pisa stabile. Cambiando la notazione è possibile condensare queste torri ed esprimere concetti più alti.

Seguire le frecce

Sviluppare un altro modo per indicare le potenze:

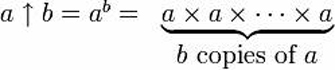
Donald Knuth ha coniato un nuovo operatore per l’esponenziazione ripetuta (“tetrazione”), per riportare quelle torri di potenza sulla terra.

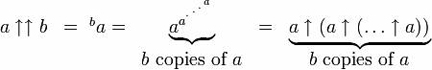
In uso, la doppia freccia si presenta così:

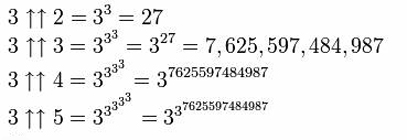
Questo può essere esteso ulteriormente aggiungendo una terza freccia, creando l’operazione di “pentazione” – tetrazione ripetuta.

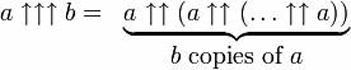
In parole, ciò comporta la tetrazione di a all’a (quindi, una torre di potenza di un ‘a’), poi costruire un’altra torre di ‘a’ alta quanto quella torre di potenza, poi usando il risultato di quella torre di potenza per determinare il numero di ‘a’ nella prossima – con il risultato di calcolare b torri di potenza, aumentando in altezza secondo il risultato della precedente tetrazione.

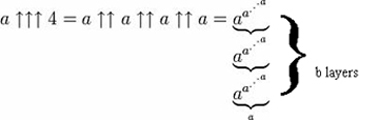
E si possono ancora aggiungere altre frecce, anche se pensare alle operazioni che denotano può richiedere più tempo del cervello di quanto si sia disposti a dedicare alla questione. Ma armati di questa notazione, possiamo ora riconoscere alcuni numeri veramente grandi.

Chiamando Ackermann e Graham

Le prove matematiche ci hanno dato delle quantità enormi. All’inizio del ventesimo secolo, i matematici volevano sapere come dire se una sequenza era calcolabile – si poteva definire un processo meccanico per elaborarla? Fu proposto che una sequenza fosse calcolabile se aveva la proprietà di essere “ricorsiva primitiva”. Wilhelm Ackermann mise una pietra sopra alla sequenza coniando una sequenza che, pur essendo calcolabile, non era ricorsiva primitiva. E fa così:

Inizia con l’operazione matematica più semplice possibile: l’addizione. Applicala al primo numero naturale, 1:

1 + 1 = 2

Poi passa all’operazione successiva, la moltiplicazione (aggiunta ripetuta). Fallo per il prossimo numero:

2 × 2 = 4

Il prossimo passo è la moltiplicazione ripetuta – l’esponenziazione per voi e per me – con 3 come variabile.

33 = 27

Fin qui, tutto molto semplice. Ma abbiamo appena definito una funzione per l’esponenziazione ripetuta, la tetrazione, e se lo facciamo a 4..

Sembra piccolo, ha 10154 cifre. E questo è solo il 4° termine della sequenza.

Il quinto è … una torre di potenza di cinque cifre.

Il sesto è . Solo cinque simboli denotano un numero più grande di quanto ci sia spazio nell’universo, anche se si scrivesse ogni cifra in un carattere largo 1nm. E la sequenza continua.

La stessa notazione con le frecce verso l’alto fu usata da Ronald Graham per limitare alcune proprietà di un ipercubo (un cubo in 4 dimensioni spaziali), anche se il ‘numero di Graham’ è ora meglio conosciuto semplicemente per essere collossale.

Il numero di Graham è definito così:

Il numero di frecce in ogni strato è dato dal risultato della valutazione delle frecce nello strato sottostante, finché dopo 64 strati si raggiunge il numero finale. Per darvi un’idea delle dimensioni di questo, possiamo guardare solo il primo strato:

dove il numero di tre nell’espressione a destra è

Ora ogni operazione di tetrazione () si riduce a una “torre” di esponenziazioni () secondo la definizione

dove ci sono X tre.

Quindi,

dove il numero di tre è , diventa, solo in termini di “torri di esponenziazione” ripetute, e dove il numero di tre in ogni torre, a partire dalla torre più a sinistra, è specificato dal valore della torre successiva a destra.

Questo è, tecnicamente parlando, un sacco di tre. Non rilassatevi ancora, però, perché il numero di Graham, pur essendo il più grande numero che i matematici abbiano ancora avuto bisogno di scrivere esplicitamente, è nanizzato da alcuni prodotti della teoria dei calcoli. Non abbiamo spazio per approfondirli qui, ma date un’occhiata a “Chi può scrivere il numero più grande?” di Scott Aaronson se il numero di Graham non vi basta. Approfondisce anche la storia dei grandi numeri e le loro spiegazioni.

Grande, più grande, più grande

Il mondo dei numeri è, come ci si potrebbe aspettare, infinito. La natura è piuttosto grande, ma i numeri che ci chiede di usare sono molto più piccoli di quelli che i matematici umani hanno sognato. In questo senso, la mente umana è più grande dell’universo.