Stiramento orizzontale -Proprietà, grafico ed esempi

Potresti aver già incontrato grafici che si assomigliano ma che hanno larghezze diverse. Queste funzioni possono essere state allungate orizzontalmente usando una funzione base. Gli stiramenti orizzontali sono tra le tecniche di trasformazione più applicate quando si graficano le funzioni, quindi è meglio capirne la definizione.

Gli stiramenti orizzontali avvengono quando un grafico di base viene allargato lungo l’asse x e lontano dall’asse y.

Imparare come possiamo stirare i grafici orizzontalmente può aiutarci a capire la famiglia dei grafici delle funzioni. Possiamo anche imparare come velocizzare la rappresentazione grafica di nuove funzioni in base ai fattori di scala applicati.

Assicuratevi di rivedere la vostra conoscenza delle funzioni madri, delle traslazioni e degli allungamenti verticali prima di passare alla prossima sezione.

• Comprendere le funzioni madri comuni che potremmo incontrare.
• Rinfrescare la vostra conoscenza delle trasformazioni verticali e orizzontali.
• Ripassare come applicare gli allungamenti verticali.

Questi articoli collegati possono aiutarti a rinfrescare le tue conoscenze, e quando sei pronto, andiamo avanti e impariamo di più sullo stretching orizzontale.

Che cos’è uno stretching orizzontale?

Possiamo applicare lo stretch orizzontale ad una funzione moltiplicando i suoi valori di input per un fattore di scala, a, dove 0 < 1/a < 1. Cosa significa questo per funzioni come f(x)? Quando 1/a viene moltiplicato per x, il grafico di f(x) si allunga orizzontalmente di un fattore di scala di a.

Andiamo avanti e vediamo come f(x) = x2 sarà influenzata da un fattore di scala di 1/2 e 1/3.

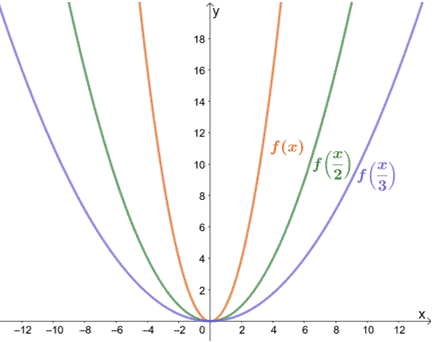
Come ci aspettavamo, il grafico si allunga di un fattore 2 e 3. Notate come i valori y rimangono gli stessi? Questo è vero per tutti gli allungamenti orizzontali. Il grafico si allunga solo lontano dall’asse y quando allunghiamo orizzontalmente un grafico.

L’allungamento orizzontale su altre funzioni mostrerà proprietà simili. Diciamo che abbiamo f(x) = |x|, se il grafico di questa funzione deve essere allungato orizzontalmente per ottenere g(x), la nuova espressione della funzione può essere espressa come |1/3 ∙ x| = |x/3|.

Perché non confrontiamo alcuni valori delle due funzioni?

x	-2	-1	0	1	2
f(x) = |x|	2	1	0	1	2

Ci aspettiamo anche che tutte le sue coordinate x-aumentino di 3. Quando facciamo questo, i valori di uscita rimarranno gli stessi.

x	-6	-3	0	3	6
g(x) = |x/3|	2	1	0	1	2

Cosa significa questo per le coordinate del grafico della nuova funzione? Se la funzione f(x) passa per (m, n) e viene allungata orizzontalmente di un fattore 1/a, la nuova funzione passerà per (am, n).

Come allungare orizzontalmente una funzione?

Ora che abbiamo imparato gli allungamenti orizzontali e come influenzano una funzione base, è il momento di applicarli ai grafici delle funzioni. Prima di iniziare ad allungare le funzioni orizzontalmente di un certo fattore, ricordate queste indicazioni per allungare i grafici più velocemente in orizzontale:

• Solo allungare la base del grafico orizzontalmente in modo che le coordinate y rimangano nella stessa posizione.
• Siccome le coordinate y rimarranno le stesse, anche l’intercetta y rimarrà la stessa.
• Assicurati di ricontrollare i punti critici del grafico, come le sue intercette, i punti massimi, e altro.
• Vedi se anche i punti delle coordinate sono scalati correttamente.

Utilizziamo la tabella di valori mostrata nella sezione precedente per tracciare il grafico di y = |x| e y = |x/3| per visualizzare gli effetti di un tratto orizzontale su un grafico.

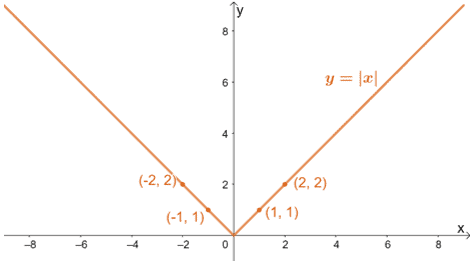
Come abbiamo discusso, ci aspettiamo che i grafici si allunghino lungo la base con i valori di y che rimangono costanti.

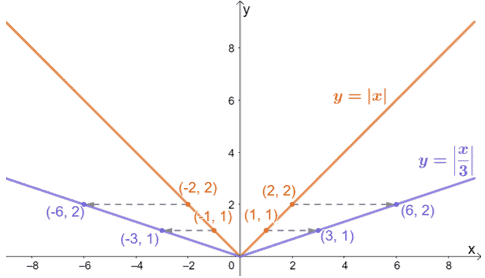
Per ottenere y = |x/3|, allunghiamo la funzione madre y = |x| di un fattore 3. Il grafico mostrato sopra lo conferma, e possiamo applicare lo stesso processo quando allunghiamo orizzontalmente i grafici di altre funzioni. Riassumiamo quello che abbiamo imparato finora prima di provare altre domande.

Riassunto della definizione e delle proprietà dello stiramento orizzontale

Queste sono alcune indicazioni importanti da ricordare quando si risponde a problemi e si tracciano grafici di funzioni che comportano uno stiramento orizzontale:

• Si può stirare orizzontalmente un grafico di un fattore 1/a solo quando anche il valore di ingresso è aumentato di a.
• Quando f(x) viene allungata orizzontalmente in f(ax), moltiplicare le coordinate x per a.
• Mantenere la posizione delle intercette y.
• La funzione risultante avrà lo stesso intervallo ma potrebbe avere un dominio diverso.
• Dato un punto (m, n), esso diventa (am, n) se allungato orizzontalmente.

Torniamo sempre a questi cinque punti quando siamo in dubbio. Essere in grado di padroneggiare la tecnica dello stiramento orizzontale dei grafici può aiutarci a tracciare i grafici di funzioni più velocemente e a capire il loro comportamento.

Sei pronto a mettere alla prova le tue conoscenze? Andiamo avanti e proviamo alcuni di questi problemi!

Esempio 1

La funzione g(x) si ottiene allungando orizzontalmente f(x) = 8x con un fattore di scala di 1/4. Quale delle seguenti è l’espressione corretta per g(x)?

a. g(x) = 32x
b. g(x) =16x
c. g(x) = 2x
d. g(x) =1/2 x

Soluzione

Ricordiamo che quando allunghiamo orizzontalmente una funzione di 1/a, dividiamo il valore di ingresso per a. Perché non applichiamo questo al problema? Sostituiamo x con x/4 per trovare l’espressione di g(x).

g(x) = 8(x/4)

Semplificando l’espressione si ottiene g(x) = 2x.

Esempio 2

Scrivere le espressioni per g(x) e h(x) in termini di f(x) date le seguenti condizioni:

a. La funzione g(x) è il risultato dell’allungamento orizzontale di f(x) di un fattore 1/5.
b. Quando allunghiamo orizzontalmente g(x) di un fattore di scala di 1/2, otteniamo h(x).

Soluzione

Iniziamo con g(x). Possiamo allungare orizzontalmente f(x) per ottenere g(x), quindi dividiamo il valore di ingresso di f(x) per 5 per ottenere l’espressione di g(x): f(x/5).

Ora che abbiamo g(x), possiamo trovare l’espressione per h(x). Dividiamo il valore di ingresso di g(x) per 2. Quindi, abbiamo:

h(x) = g(x/2)

= f(x/5 -1/2 )

= f(x/10)

Questo significa che in termini di f(x), g(x) = f(x/5) e h(x)= f(x/10).

Esempio 3

La funzione f(x) passa per il punto (6, 4). Se f(x) viene allungata orizzontalmente di un fattore di scala di 1/2, quale sarebbe la nuova coordinata x del punto?

Soluzione

Quando allunghiamo orizzontalmente un grafico, moltiplichiamo l’ascissa della funzione base per il denominatore del fattore di scala dato per trovare il nuovo punto che giace lungo la stessa ascissa.

Quindi, abbiamo (6, 4) → (2 ∙ 6, 4). La nuova coordinata x del punto sarà (12, 4).

Esempio 4

La tabella dei valori di f(x) è mostrata sotto. Se h(x) è il risultato dell’allungamento orizzontale di f(x) di un fattore di scala di 1/4, costruisci la sua tabella di valori e mantieni i valori di uscita attuali.

x	-3	-2	-1	0	1	2	3
f(x)	-6	-4	-2	0	2	4	6

Soluzione

Quando la funzione è allungata orizzontalmente, moltiplichiamo i valori di input (in questo caso, sono i valori di x) per il denominatore del fattore di scala dato.

Questo significa che (-2, -4) sarà trasformato in (4∙ -2, -4) = (-8, -4). Applichiamo lo stesso processo per il resto dei valori e abbiamo la tabella dei valori di h(x) come mostrato qui sotto.

x	-12	-8	-4	0	4	8	12
h(x)	-6	-4	-2	0	2	4	6

Esempio 5

Osserva le funzioni mostrate sotto. Qual è la relazione tra f(x) e g(x)?

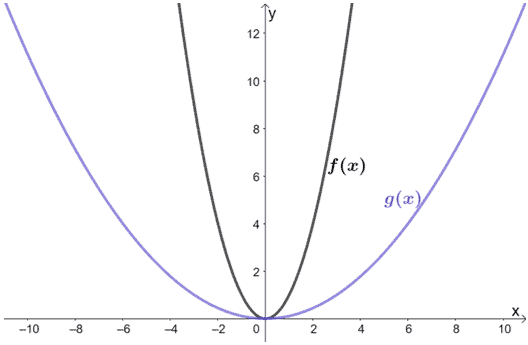
Soluzione

Solo guardando il grafico, possiamo vedere che g(x) risulta da f(x) allungata orizzontalmente. Perché non esaminiamo alcuni punti di entrambi i grafici?

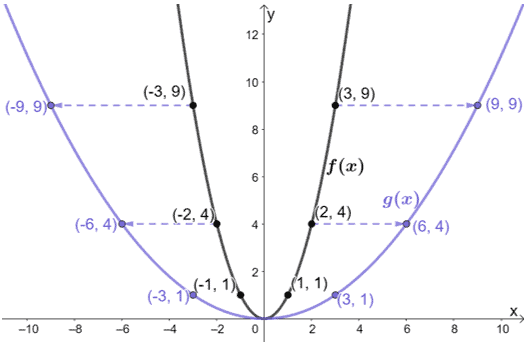
Ecco cosa succede ai punti:

• (-3, 9) → (-9, 9)
• (-2, 4) → (-6, 4)
• (-1, 1) → (-3, 1)
• (0, 0) → (0, 0)
• (1, 1) → (3, 1)
• (2, 4) → (6, 4)
• (3, 9) → (9, 9)

Nota come per ogni caso: le coordinate x di g(x) sono tutte tre volte più grandi di f(x). Questo significa che il fattore di scala usato per allungare f(x) è 1/3.

La funzione g(x) è il risultato dell’allungamento orizzontale di f(x) con un fattore di scala di 1/3.

Esempio 6

L’immagine sottostante mostra il grafico di f(x). Fai il grafico di g(x) usando il fatto che è il risultato di f(x) allungata orizzontalmente di un fattore 1/2. Assicurati di includere i nuovi punti critici di g(x).

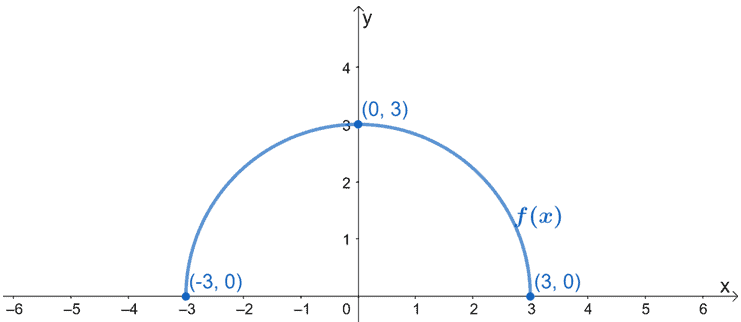
Soluzione

Per prima cosa troviamo i nuovi punti critici di g(x). Poiché f(x) sarà allungata orizzontalmente, moltiplicheremo le coordinate x per 2. Quindi, abbiamo i seguenti punti critici:

• (-3, 0) → (-6, 0)
• (0, 3) → (0, 3)
• (3, 0) → (6, 0)

Plottare questi punti e allungare il grafico di f(x) di 3. Assicurati che le coordinate y e l’intercetta y rimangano le stesse.

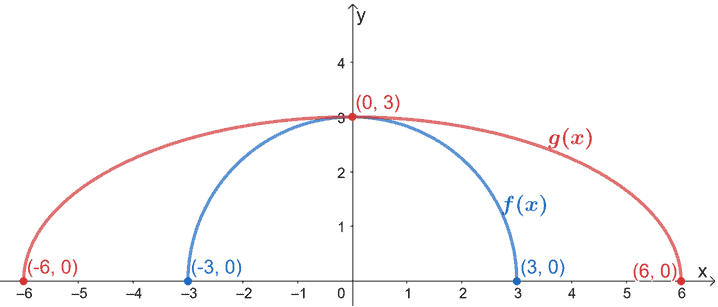
Ecco come dovrebbe apparire il grafico risultante. Poiché g(x) è il risultato dell’allungamento orizzontale di f(x), allunghiamo il grafico di f(x) di una scala di 3.

Esempio 7

Descrivi le trasformazioni fatte sulle seguenti funzioni mostrate qui sotto.

a.f(x) = x2 → g(x) = x2/9

b. m(x) = √x → n(x) = 3√(x/4)
c. p(x) = 3x – 1→ q(x) = 3x/4 – 2

Soluzione

Se hai notato che alcune possono non presentare solo tratti orizzontali, hai ragione!

Tieni presente che a volte dobbiamo applicare diverse tecniche di trasformazione per ottenere l’espressione di una particolare funzione.

Primo, cominciamo con f(x) e g(x):

Per controllare il fattore di scala applicato nel valore di ingresso di f(x) per ottenere g(x), esprimiamo g(x) come un quadrato perfetto: g(x) = (x/3)2 = (1/3 – x)2.

Esprimendo g(x) in termini di f(x), abbiamo g(x) = f(x/3). Quindi, g(x) è il risultato dell’allungamento orizzontale di f(x) con un fattore di scala di 1/3.

Passiamo a m(x) e n(x):

Vediamo due fattori di scala applicati a n(x): 3 sul valore di uscita e 1/4 per quello di ingresso. Applicando ciò che sappiamo sui tratti verticali e orizzontali, abbiamo n(x) = 3-m(1/4 – x). Cioè, n(x) è il risultato di m(x) allungato verticalmente di un fattore di scala 3 e orizzontalmente di un fattore di scala 1/4.

Infine, osserviamo le traslazioni fatte su p(x).

q(x) = 3/4 x – 1 – 1

= 3(x/4) – 1 – 1

= p(x/4) – 1

Da questo, possiamo vedere che q(x) risulta da p(x) allungata orizzontalmente di un fattore di scala di 1/4 e traslata di una unità verso il basso.

Esempio 8

Quali sono le trasformazioni fatte su f(x) in modo che risulti g(x) = 2|x/3| – 1? Usa il grafico di f(x) mostrato qui sotto per guidarti. Applica le trasformazioni al grafico di g(x).

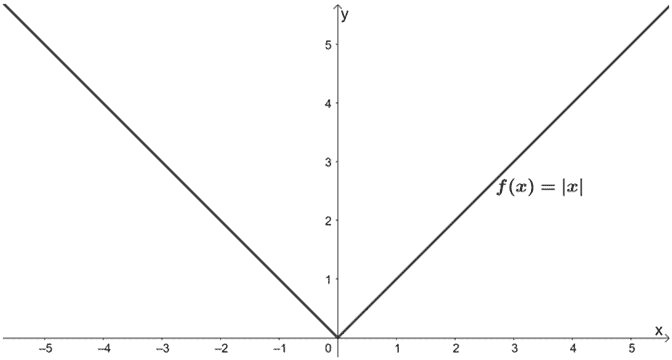
Soluzione

Andiamo avanti ed esprimiamo g(x) in termini di f(x).

g(x) = 2 – |1/3 – x| – 1

= 2- f(x/3) – 1

Questo significa che le traslazioni su f(x) per ottenere g(x) sono:

• Teso orizzontalmente di un fattore di scala di 1/3.
• Teso verticalmente di un fattore di scala di 2.
• Traslato verso il basso di 1 unità.

Applichiamo lentamente queste trasformazioni su f(x), iniziando con lo stiramento orizzontale di f(x).

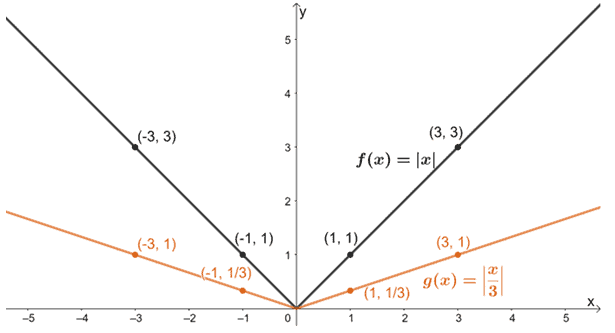
Stendiamo ora il grafico risultante verticalmente di un fattore di scala 2.

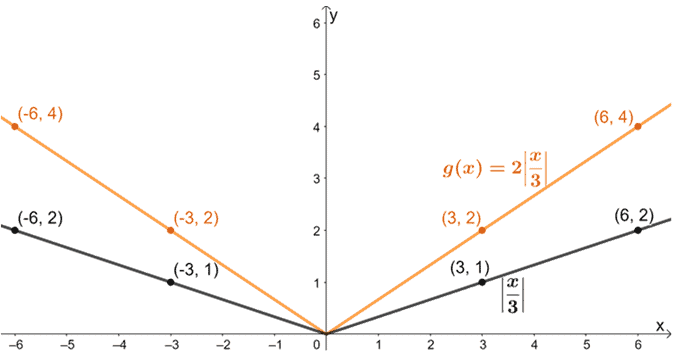
Infine, traduciamo il grafico di una unità verso il basso.

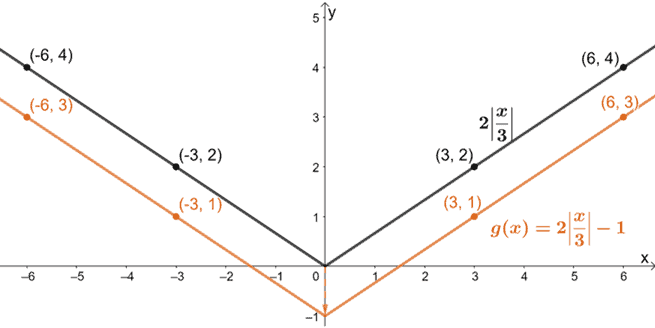
Allora, abbiamo appena mostrato come g(x) può essere rappresentata graficamente usando la funzione madre delle funzioni di valore assoluto, f(x) = |x|.

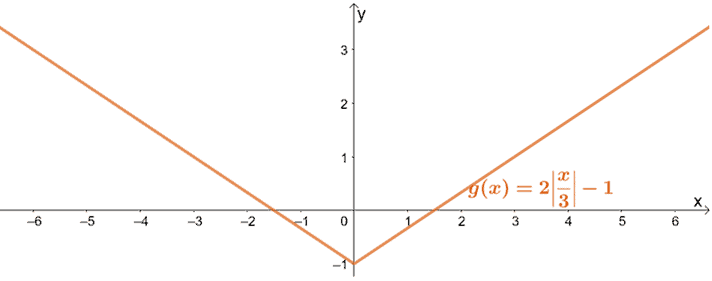
Domande pratiche

1. La funzione g(x) si ottiene allungando orizzontalmente f(x) = 16×2 di un fattore di scala 2. Quale delle seguenti è l’espressione corretta per g(x)?

a. g(x) = 32×2

b. g(x) = 16×2

c. g(x) = 8×2

d. g(x) = 2×2

2. Scrivi le espressioni per g(x) e h(x) in termini di f(x) date le seguenti condizioni:

a. La funzione g(x) è il risultato dell’allungamento orizzontale di f(x) di un fattore 1/4.

b. Quando allunghiamo orizzontalmente g(x) di un fattore di scala di 1/3, otteniamo h(x).

3. La funzione f(x) passa per il punto (10, 8). Se f(x) viene allungata orizzontalmente di un fattore di scala di 5, quale sarebbe la nuova coordinata x del punto?

4. La tabella dei valori di f(x) è mostrata sotto. Se g(x) è il risultato dell’allungamento orizzontale di f(x) di un fattore di scala 3, costruisci la sua tabella dei valori e mantieni i valori di uscita attuali.

x	-9	-6	-3	0	3	6	9
f(x)	-17	-11	-5	1	7	13	19

5. Osservate le funzioni mostrate qui sotto. Qual è la relazione tra f(x) e g(x)?

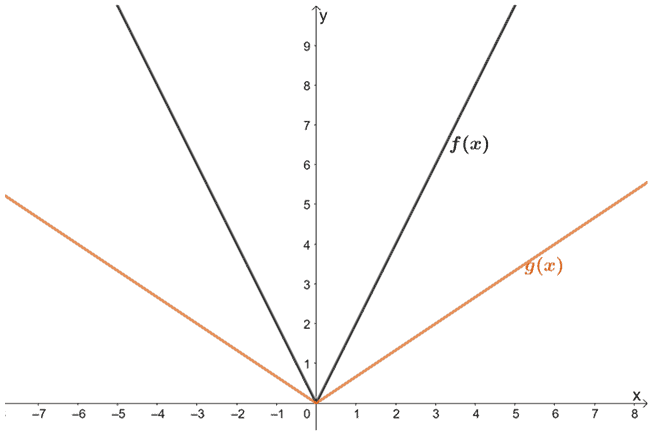
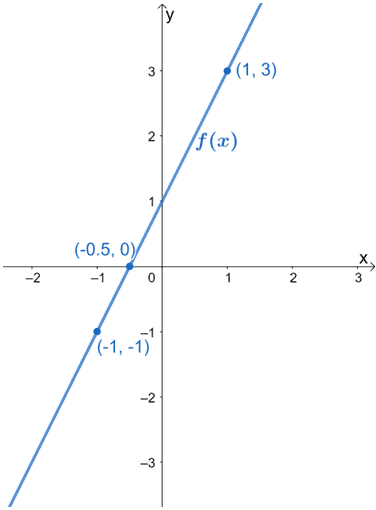
6. L’immagine sottostante mostra il grafico di f(x). Fai il grafico di h(x) usando il fatto che è il risultato dell’allungamento orizzontale di f(x) di un fattore 1/3. Assicurati di includere i nuovi punti critici per g(x).

7. Descrivi le trasformazioni effettuate sulle seguenti funzioni mostrate qui sotto.

a. f(x) = x2 → g(x) = x2/16

b. m(x) = √x → n(x) = √(x/5) + 3

c. p(x) = 2x + 1→ q(x) = 2x/3 + 2

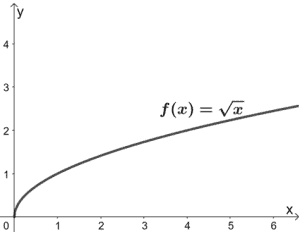
8. Quali sono le trasformazioni fatte su f(x) in modo da ottenere g(x) = 3√(x/2)? Usa il grafico di f(x) mostrato qui sotto per guidarti. Applicare le trasformazioni al grafico di g(x).

Le immagini/i disegni matematici sono creati con GeoGebra.