回帰問題に最適な機械学習アルゴリズムを選択する

私は最近、本に焦点を当てた教育的なニュースレターを始めました。隔週で配信しています。 Book Dives」は隔週で発行されるニュースレターで、新しい号のたびにノンフィクションの本にダイブします。 このニュースレターでは、隔週でノンフィクションの本を取り上げ、その本の核となる教訓と、それを実際の生活に応用する方法を紹介しています。

機械学習（ML）の問題に取り組む際には、さまざまなアルゴリズムから選択する必要があります。 機械学習では、「フリーランチのない定理」と呼ばれるものがあり、基本的に、すべての問題に最適なMLアルゴリズムはないとされています。 さまざまなMLアルゴリズムの性能は、データのサイズや構造に強く依存します。

しかし、それぞれのMLアルゴリズムには長所と短所があり、それを参考にすることができます。 あるアルゴリズムが常に他のアルゴリズムより優れているというわけではありませんが、正しいアルゴリズムを迅速に選択し、ハイパーパラメータをチューニングする際のガイドとして利用できる、各アルゴリズムの特性があります。 これから、回帰問題のためのいくつかの著名なMLアルゴリズムを見て、その長所と短所に基づいて、いつ使用するかのガイドラインを設定します。

この記事は、回帰問題に最適なMLアルゴリズムを選択する際の大きな助けとなるはずです！

本題に入る前に、AI、機械学習、データサイエンスに関する最新かつ最高の情報を読むために、AI Smart Newsletterをチェックしてみてください。

線形回帰と多項式回帰

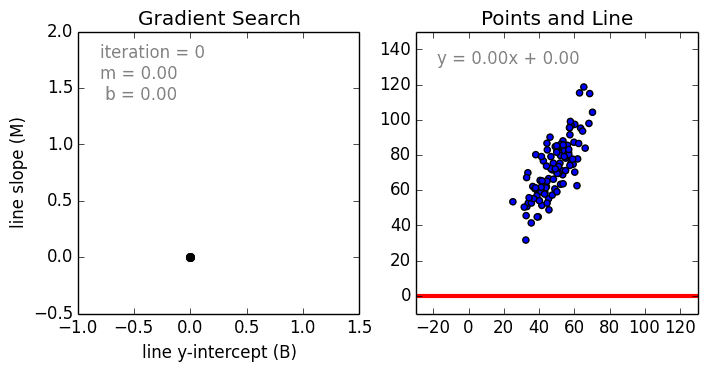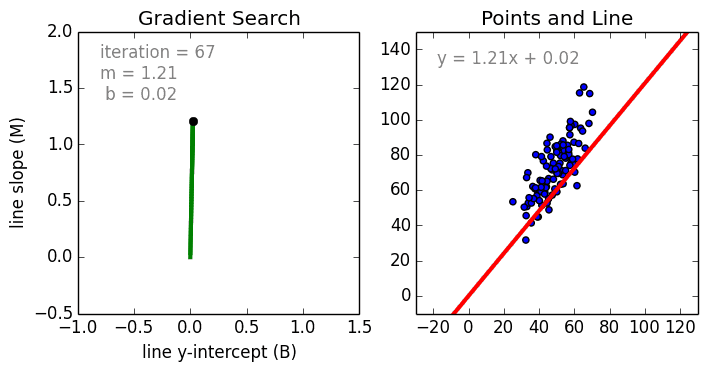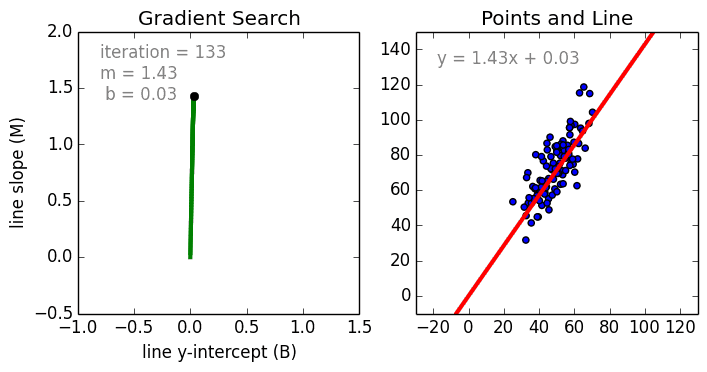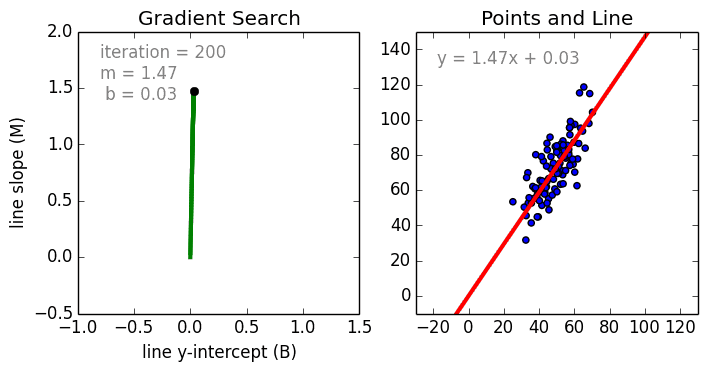
まず、単純なケースから。 単一変数線形回帰は、単一の入力独立変数（特徴変数）と出力従属変数の間の関係を、線形モデル（直線）を使用してモデル化するために使用される手法です。つまり、直線です。 より一般的なケースは、多変数線形回帰で、複数の独立した入力変数（特徴変数）と出力従属変数の間の関係のモデルを作成します。

最も一般的なケースとして、モデルが特徴変数の非線形な組み合わせになる多項式回帰というものがあります（指数変数、サインとコサインなど）。 しかし、これには、データと出力の関係についての知識が必要です。

長所：

• モデル化が速く、モデル化される関係が極端に複雑でなく、データ量が多くない場合に特に役立ちます。
• 線形回帰は理解しやすく、ビジネス上の意思決定に非常に役立ちます。

Cons:

• 非線形データの場合、データの構造や特徴変数間の関係に関する情報が必要となるため、多項式回帰の設計は非常に困難になります。
• 以上の結果、これらのモデルは、非常に複雑なデータに関しては、他のモデルよりも優れていません。

ニューラルネットワーク

iv

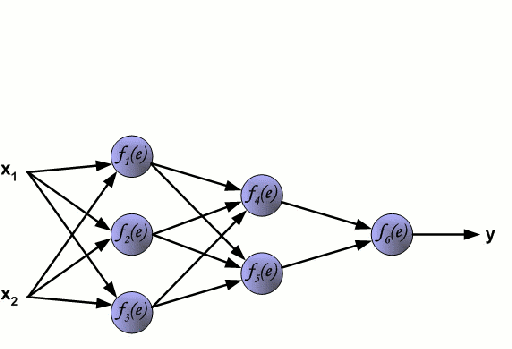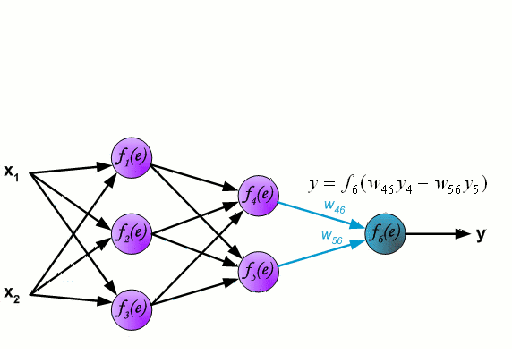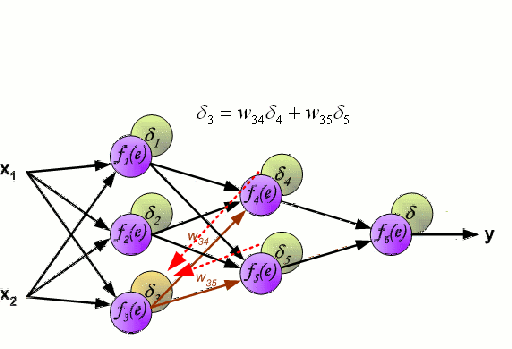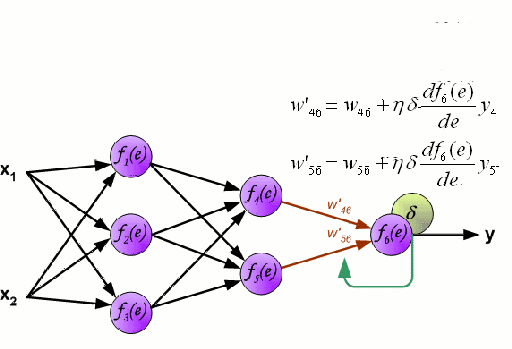
ニューラルネットワークは、ニューロンと呼ばれるノード群が相互に接続されて構成されています。 データからの入力特徴変数は、多変数の線形結合としてこれらのニューロンに渡され、各特徴変数に乗算された値は重みとして知られています。 そして、この線形結合に非線形性を適用することで、ニューラルネットワークは複雑な非線形関係をモデル化することができます。 ニューラルネットワークは複数の層を持つことができ、ある層の出力は同じように次の層に渡されます。 出力には、通常、非線形性は適用されません。

Pros:

• ニューラル ネットワークは、非線形性を持つ多くの層 (およびそのためのパラメータ) を持つことができるため、非常に複雑な非線形関係をモデル化するのに非常に効果的です。
• ニューラル ネットワークは、ほぼすべての種類の特徴変数の関係を学習する上で非常に柔軟であるため、一般的にデータの構造を心配する必要はありません。
• 研究では、まったく新しいものであれ、元のデータ セットを補強したものであれ、ネットワークにより多くのトレーニング データを与えるだけで、ネットワークのパフォーマンスが向上することが一貫して示されています。

Cons:

• これらのモデルは複雑であるため、解釈や理解が容易ではありません。
• これらのモデルは、慎重なハイパーパラメータのチューニングと学習率スケジュールの設定を必要とするため、学習するのが非常に難しく、計算負荷が高い場合があります。
• これらのモデルは、高いパフォーマンスを達成するために多くのデータを必要とし、「小さなデータ」のケースでは、一般的に他の ML アルゴリズムよりも優れたパフォーマンスを発揮します。

Regression Trees and Random Forests

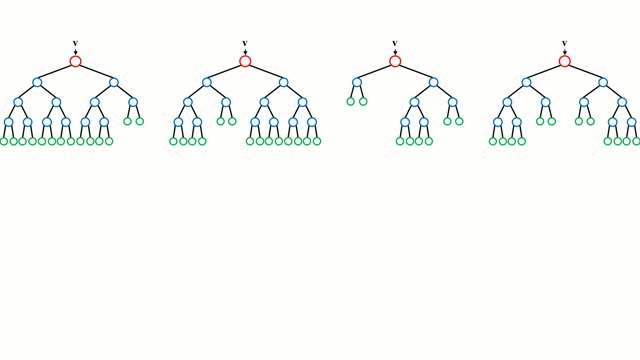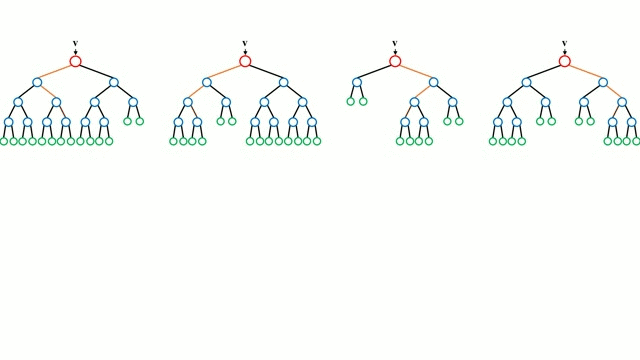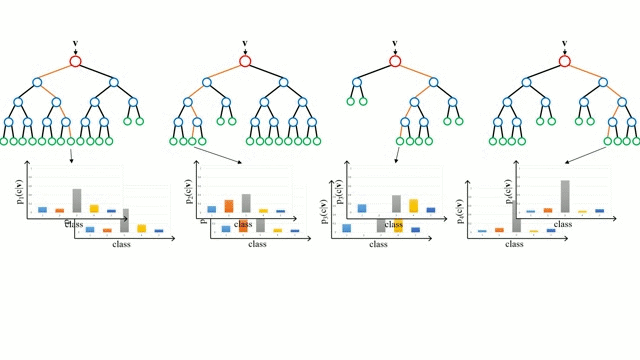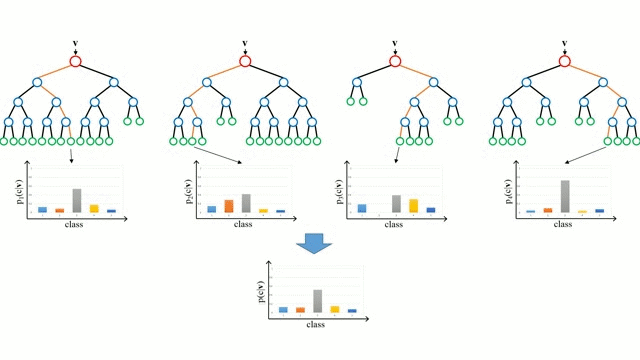
まず、ベースケースから始めます。 決定木とは、木の枝を辿り、ノードでの決定に基づいて次の枝を選択する直感的なモデルです。 ツリー誘導とは、トレーニングインスタンスを入力とし、どの属性で分割するのが最適かを決定し、データセットを分割し、すべてのトレーニングインスタンスが分類されるまで、分割されたデータセットを繰り返し処理する作業です。 ツリーを構築する際の目標は、可能な限り純粋な子ノードを作成する属性で分割することで、データセット内のすべてのインスタンスを分類するために必要な分割の数を最小限に抑えることです。 純度は、情報利得の概念によって測定されます。情報利得とは、以前に見たことのないインスタンスを適切に分類するために、そのインスタンスについてどれだけのことを知る必要があるかということに関連します。 実際には、エントロピー (現在のデータセット パーティションの 1 つのインスタンスを分類するために必要な情報量) と、現在のデータセット パーティションが特定の属性でさらにパーティションされた場合に 1 つのインスタンスを分類するための情報量を比較することで測定されます。 入力ベクトルを複数の決定木に通します。

Pros:

• 複雑で高度に非線形な関係を学習するのに適しています。 通常、かなり高いパフォーマンスを達成でき、多項式回帰よりも優れており、多くの場合、ニューラル ネットワークと同等です。
• 解釈と理解が非常に容易です。

Cons:

• 決定木のトレーニングの性質上、大幅なオーバーフィッティングが発生しやすい。 完成した決定木モデルは過度に複雑で、不必要な構造を含むことがあります。
• 高いパフォーマンスを得るために大きなランダム フォレスト アンサンブルを使用すると、速度が低下し、より多くのメモリを必要とするという欠点があります。

結論

Boom! これで長所と短所がわかりました。 次回の記事では、さまざまな分類モデルの長所と短所を見ていきます。 この記事を読んで、何か新しいことや役に立つことを学んでいただけましたら幸いです。 楽しんでいただけたなら、遠慮なく拍手をお願いします

。