大学代数
学習成果
- 対数形から指数形への変換
- 指数形から対数形への変換。
地震の大きさを分析したり、2つの異なる地震の大きさを比較したりするためには、対数形と指数形の変換ができる必要があります。 例えば、ある地震で放出されたエネルギー量が、別の地震で放出されたエネルギー量の500倍であったとします。 その大きさの違いを計算したいとします。 この問題を表す方程式は{10}^{x}=500で、xはリヒタースケールでのマグニチュードの差を表します。
私たちはまだ指数方程式を代数的に解く方法を学んでいません。 10}^{x}=500を解くには、これまでに説明したどの代数的手段も十分ではありません。 10}^{2}=100と{10}^{3}=1000を知っているので、y={10}^{x}が増加していることからxは2と3の間のある値でなければならないことは明らかです。
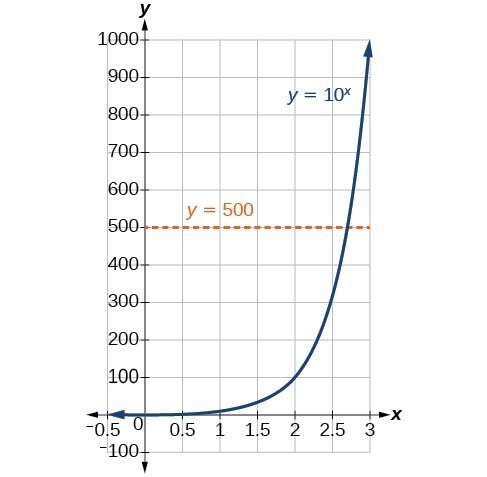
しかしながら、グラフからの推定は不正確です。 代数的な解を求めるためには、新しい関数を導入する必要があります。 上のグラフが水平線検定に合格していることを確認してください。 指数関数y={b}^{x}は一対一なので、その逆関数x={b}^{y}も関数です。 すべての逆関数の場合と同様に、xとyを入れ替えてyを解くことで逆関数を求めることができます。 yをxの関数として表すには、y={˶‾᷅᷅˵}_{b}_left(x˶‾᷄˵)という形の対数関数を使います。
対数式を「xの底bの対数はyに等しい」と読んだり、簡略化して「xの底bの対数はyである」と言ったりします。 また、対数は指数であるため、「bをyの累乗にするとxになる」とも言えます。 例えば、32の基数2対数は5です。なぜなら、5は32を得るために2に適用しなければならない指数だからです。 2}^{5}=32なので、 {\mathrm{log}}_{2}32=5 と書くことができます。 これを「32の対数基数2は5」と読みます。”
対数形とそれに対応する指数形の関係を以下のように表現できます。
{{mathrm{log}}_{b}\left(x\right)=y\Leftrightarrow {b}^{y}=x,\{}b>0,b\ne 1
基数bは常に正であることに注意してください。
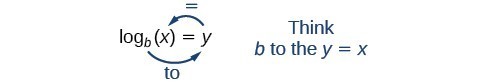
対数は関数なので、f\left(x\right)と同じように、括弧を使って関数の評価を表し、{mathrm{log}}_{b}_left(x\right)と書くのが最も正しいです。 ただし、入力が単一の変数や数値の場合は、括弧を外して {\mathrm{log}}_{b}x のように記述するのが一般的です。
対数の表記を例示すると次のようになります。
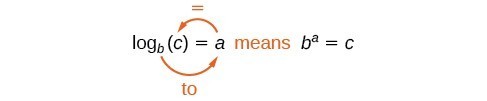
一般論:対数関数の定義
正数xの対数基数bは次の定義を満たします。
For x>0,b>0,b\ne 1,
y={mathrm{log}}_{b}left(x\right)}text{ is equal to }{b}^{y}=x, ここで、
- {mathrm{log}}_{b}_left(x\\right)を、「xの底bの対数」または「xの底bの対数」と読みます。”
- 対数 y は x を得るために b を上げなければならない指数である。
- 基数 b が示されていない場合、対数の基数は 10 と仮定される。
また、対数関数と指数関数では x と y の値が入れ替わるため、指数関数の領域と範囲は対数関数と入れ替わる。 したがって、
- 基数bの対数関数のドメインは\left(0, ˶ˆ꒳ˆ˵)
- 基数bの対数関数の範囲は\left(-˶ˆ꒳ˆ˵)
divine
Q & A
負の数の対数をとることはできるか
いいえ、指数関数の底は常に正であるため、その底の累乗が負になることはありません。 そのため、負の数の対数をとることはできません。 また、ゼロの対数をとることもできません。 電卓は複素数モードの時に負の数の対数を出力することがありますが、負の数の対数は実数ではありません。
How To: How To: Have an equation in logarithmic form {\mathrm{log}}_{b}left(x\right)=y, convert it to exponential form
- 方程式y={\mathrm{log}}_{b}xを調べ、b, y, xを特定しなさい。
- {mathrm{log}}_{b}x=yを{b}^{y}=xと書き直します。
Example: 対数形から指数形への変換
以下の対数形の方程式を指数形で書いてみましょう。
- {{mathrm{log}}_{6}\left(sqrt{6}\right)=\frac{1}{2}
- {{mathrm{log}}_{3}\left(9\right)=2
Try It
以下の対数方程式を指数形式で書きなさい。
- {{mathrm{log}}_{10}}left(1,000,000right)=6
- {\mathrm{log}}_{5}\left(25\right)=2
指数形から対数形への変換
指数形から対数形への変換は、同じ手順を逆に行います。 基数b、指数x、出力yを特定し、x={\\{log}}_{b}}left(y\\right)と記述します。
Example: 指数形から対数形への変換
以下の指数方程式を対数形で書いてみましょう。
- {2}^{3}=8
- {5}^{2}=25
- {10}^{4}=\frac{1}{10,000}
Try It
以下の指数方程式を対数形式で書いてください。
- {3}^{2}=9
- {5}^{3}=125
- {2}^{-?1}=frac{1}{2}