柱の座屈方程式
このシリーズの前回の記事では、単純化された理想的な構造を使って、いくつかの基本的な概念を紹介しました。 今回の記事では、より現実的な構造を検討し、柱の座屈方程式を決定します。 特に、端部が固定された軸方向荷重の柱の限界荷重の式を決定します。
📓 この投稿は、柱の座屈に関する 3 部作のうちの 2 部です。
この記事は、柱の座屈に関する 3 つのパートのうちのパート 2 です。
この 3 つのパートは、きれいにフォーマットされた電子ブックとして無料でダウンロードできます。
この記事では、かなり多くのことを取り上げます。
- 両端で固定された柱
- 微分方程式の確立
- 微分方程式の解決
- 積分定数の解決
- のようになります。
- 座屈モードとモードシェイプ
- 限界荷重下での最大たわみ
- 高次の座屈モード
- 他の支持条件を持つ柱
- Fixed-Fixed
- Fixed-Free
- Fixed-Pinned
- 座屈の軸
- 臨界応力
- 柱の有効長
ピンサポートとは、抵抗のないサポートのことです。 これは、回転に対して抵抗のないサポートです。 実際には、この理論的な定義に非常に近いピン サポートに出会うことがあります。 以下にいくつかの例を示します。
ここでの議論の目的は。 ここでは、このようなピン サポートを扱い、構造体の回転を阻害しないと仮定します。
1.0 両端で固定された柱の座屈方程式
この構造を分析するために、![]()
![]()
![]()
![]()
![]()
![]() の積となります。
の積となります。
![]()
💡この式は、ある曲げ剛性を持つ柱のたわみ形状を単純にモデル化したものです。
この式は、工学の勉強の中でどこかで目にしたことがあると思います。 横方向にたわんだ柱は、梁とほぼ同じように振る舞います。 座屈は、直接の圧縮 (破砕) による破壊ではなく、曲げによる破壊であることを覚えておいてください。
📌 前の投稿で説明した理想化された構造の場合と同様に、ここでの導出も、構造のサイズに比べてすべての偏向が小さいと仮定します。
微分方程式の確立
まず、構造体を考えます。 たわみの形状と、構造物を切断して得られる自由な
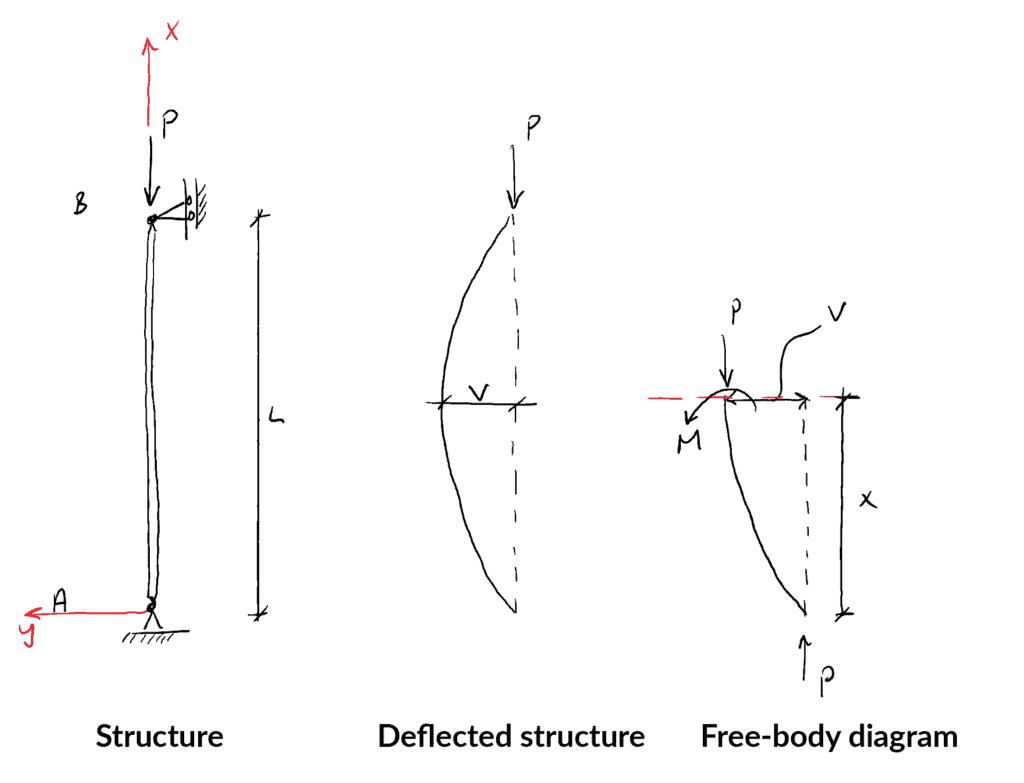
点Aについてモーメントを取ると以下のようになります。
![]()
![]() をたわみ曲線の微分方程式に戻して、少し並べ替えると次のようになります。
をたわみ曲線の微分方程式に戻して、少し並べ替えると次のようになります。
![]() {align*}。 + ¶frac{P}{EI}v=0\end{align*}
{align*}。 + ¶frac{P}{EI}v=0\end{align*}
これは、定数係数を持つ線形の同次2階微分方程式です。 また、この方程式は、構造物のたわみ形状をモデル化し、軸方向の荷重である![]()
![]() 、つまり柱の曲げ抵抗で釣り合う適用荷重の値を求めることができます。
、つまり柱の曲げ抵抗で釣り合う適用荷重の値を求めることができます。
このように、私たちは微分方程式を解こうとしています。 この時点で、この形式の微分方程式の一般的な解法を示すことができると便利です。
![]()
微分方程式を解く。
微分方程式を解く
この時点で、微分方程式がどのようにして解かれるのか、ちょっと寄り道してみたい方。 以下のビデオをご覧ください。 そうでなければ、次のセクションで積分の定数を計算することを続けます。
積分の定数を解く
この形式の方程式の一般的な解が得られたので、列の境界条件(ピンと張った状態)を使って積分の定数を解く必要があります。
境界条件 1:
![]()
![]() (横方向のたわみはゼロでなければならない)。 これらの条件を我々の一般的な解に課すと、次のようになります。
(横方向のたわみはゼロでなければならない)。 これらの条件を我々の一般的な解に課すと、次のようになります。
![]()
従って
以下のようになります。
![]()
その結果、我々の解は次のようになります。
![]()
境界条件2:
![]()
![]() (横方向のたわみもゼロ)となります。 この境界条件を適用すると、
(横方向のたわみもゼロ)となります。 この境界条件を適用すると、
![]()
つまり、![]()
![]() が0になるかです。…)
が0になるかです。…)
はゼロに等しい。 ![]()
![]() のどの値でも方程式は満たされます。 これでは、あまり前に進みません…この解はトリビアル解と考えることができます。 もっと興味深いのは、次のような場合です。
のどの値でも方程式は満たされます。 これでは、あまり前に進みません…この解はトリビアル解と考えることができます。 もっと興味深いのは、次のような場合です。
![]()
![]() の関数について知っていること。
の関数について知っていること。
![]() P
P
はゼロになる必要がありますが(他のすべての項が定義上ゼロ以外の値を持つため)、そうではないことがわかっています。 そのため、ピン留めされた列に対しては、次のように解決します。
![]()
ここで ![]()
![]() を式の主語にすることができます。
を式の主語にすることができます。
![]()
![]() …
…
![]()
![]() としても知られています。
としても知られています。
![]()
2.0 座屈モードとモードシェイプ
これまでに、座屈荷重には無限系列があり、その中で最も低いものが臨界荷重であり、オイラー座屈荷重と呼ばれることを確認しました。
これは、より高い座屈のモードに対応する荷重です。 座屈の各モードには、対応する座屈の形状があります。 これをさらに検討するには、![]() を確立した後の一般的な解決策に戻ります。
を確立した後の一般的な解決策に戻ります。
![]()
2つ目の境界条件を適用した結果、次のような関係が成立しました。
![]()
この2つの式を組み合わせると次のようになります。
![]()
for ![]()
![]() の各値に対する柱のたわみ形状を表しています。…)で定義されます。
の各値に対する柱のたわみ形状を表しています。…)で定義されます。
![]()
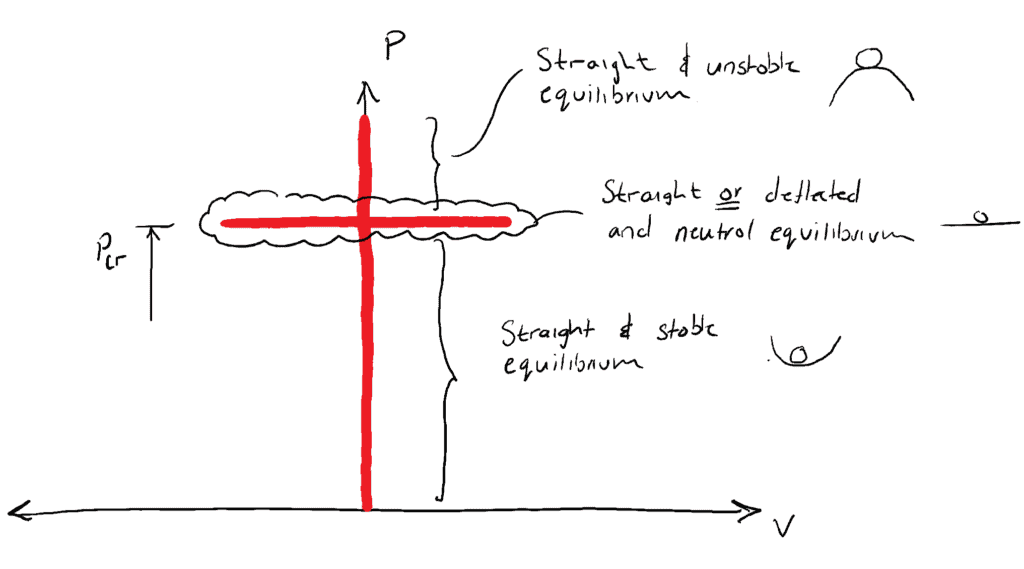
…柱が曲がった形をしていても、平衡状態であることがわかります。 他の荷重であれば、柱はまっすぐになり、STABLE(安定)な平衡状態 ![]() または UNSTABLE(不安定)な平衡状態
または UNSTABLE(不安定)な平衡状態 ![]() になります。 この概念は、前回の記事で理想的なカラム構造について説明した際に思い出しました。
になります。 この概念は、前回の記事で理想的なカラム構造について説明した際に思い出しました。
臨界荷重下での最大たわみ量
臨界荷重下での最大たわみ量 b
柱のたわみや座屈の形状を表す方程式には、パラメータ ![]()
![]() は正弦波の大きさを表し、この文脈では、偏向/座屈した偏向(上記で定義)の最大横方向の偏向を表していることがわかります。
は正弦波の大きさを表し、この文脈では、偏向/座屈した偏向(上記で定義)の最大横方向の偏向を表していることがわかります。
![]()
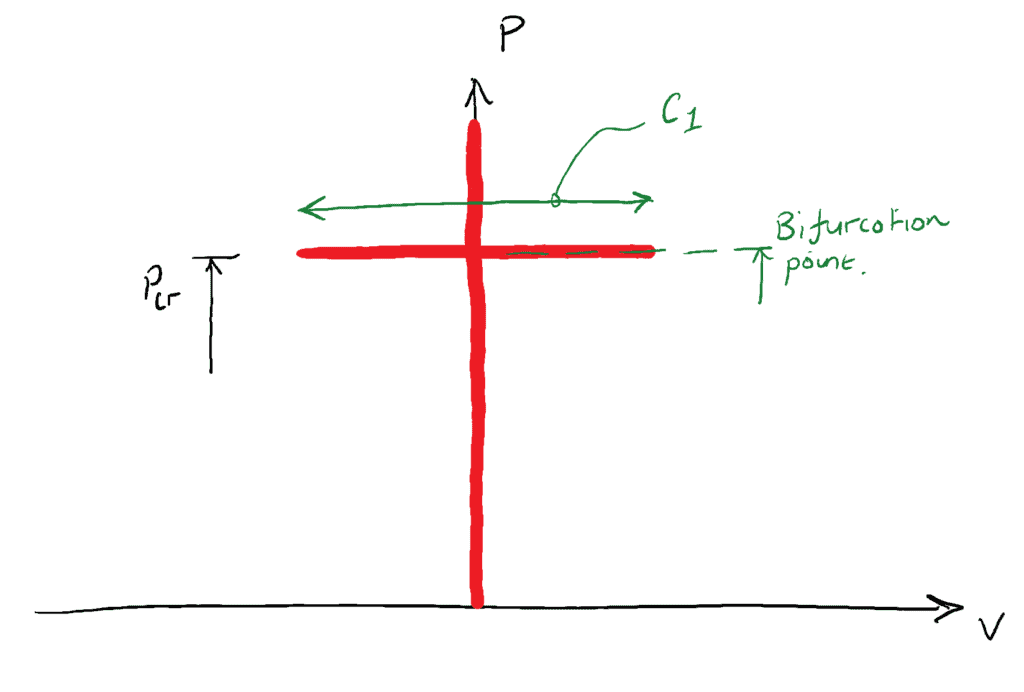
ここで、平衡状態を思い出してみましょう。 柱が座屈した状態である![]() と中立平衡状態にあるとき、最大横たわみ量は、小さなたわみ量の仮定を満たすような任意の値をとることができます。
と中立平衡状態にあるとき、最大横たわみ量は、小さなたわみ量の仮定を満たすような任意の値をとることができます。
![]()
![]() が発生した柱は故障していると考えられます。
が発生した柱は故障していると考えられます。
高次の座屈モード
軸方向に荷重を受けた固定端の柱が、その高さの中間点で横方向に拘束されていると想像してください (例えば、床スラブによって)。 柱は、横方向の拘束により、最初の臨界(オイラー座屈)荷重で座屈するのを防ぐことができます。
この拘束の結果、柱は2つ目の座屈荷重![]() に達するまで、より多くの荷重を支えることができます。
に達するまで、より多くの荷重を支えることができます。
💡適切な横方向の拘束は、低いモードでの座屈の可能性を「遮断」し、より高い座屈荷重を「解放」することで、柱の座屈に対する抵抗力を高めます。
![]() に対する荷重とたわみの形状の方程式を評価するだけで、座屈の最初の3つのモードを簡単に可視化することができます。
に対する荷重とたわみの形状の方程式を評価するだけで、座屈の最初の3つのモードを簡単に可視化することができます。
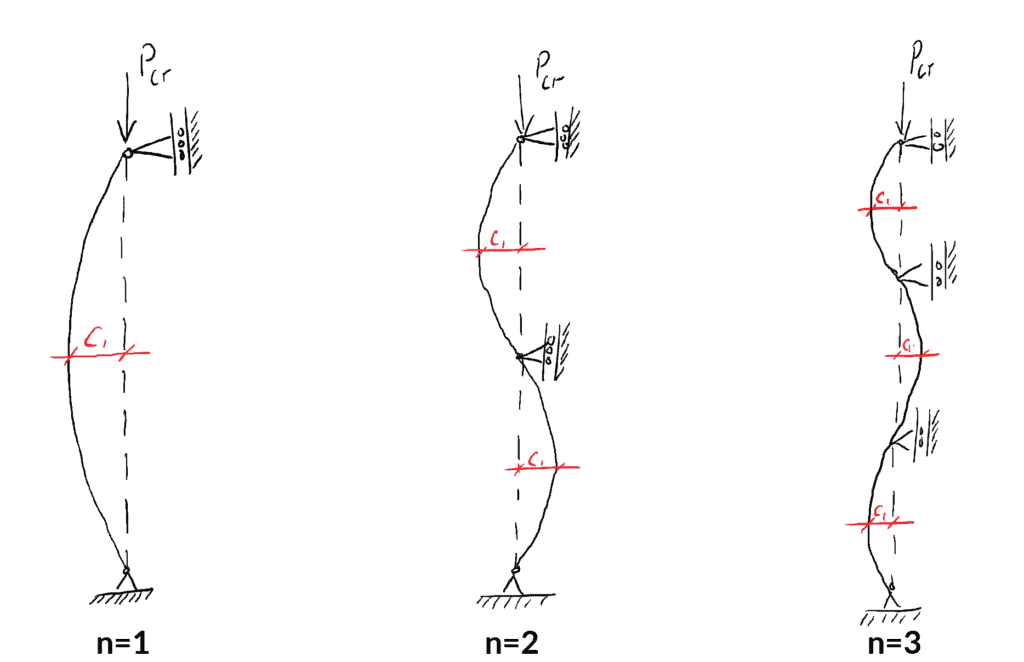
モード
div ![]()
![]()
![]()
クリティカルロード
![]()
![]()
![]()
くびれた形
![]()
![]()
![]()
![]() は軸方向の荷重の実用的な上限を表しています。
は軸方向の荷重の実用的な上限を表しています。
3.0 他の支持条件を持つ柱
これまでは、両端で固定された柱の挙動を見てきました。 これは典型的な出発点です。 しかし、同じプロセスで、異なるタイプの支持条件を持つ柱の対応する方程式を決定することができます。 以下のビデオでは、そのプロセスを実演するために導出を行っています。
- 基部が回転に対して固定され、上部が自由である柱 (fixed-free)
- 両端が回転に対して固定された柱 (fixed-fixed)
- 基部が回転に対して固定され、上部がピンで固定された柱 (fixed-pinned)
両端で回転に対して拘束された柱のバッ クリング方程式(fixed-fixed)
下部で回転に対して拘束され、上部で自由になった柱のバッ クリング方程式(fixed-free)
柱が下部で回転を拘束され、上部で固定されている場合のバックリング方程式(fixed-pinned)
支持条件のまとめ
div
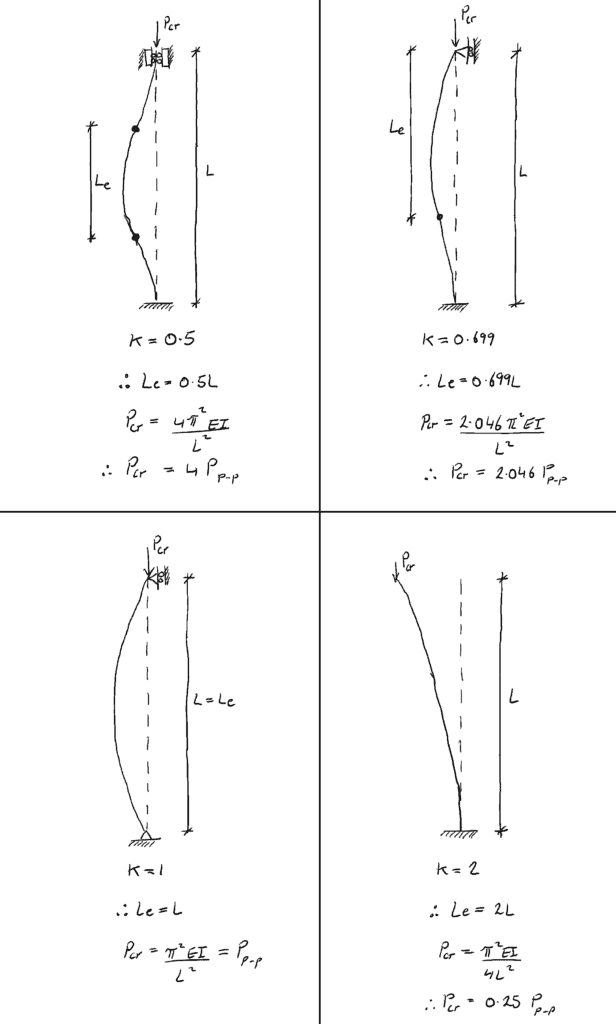
4.0 座屈の軸
座屈荷重の式から、断面積の2次モーメントであるIの関数であることを思い出します。
![]()
従って、任意の断面に対して、柱は常に面積の2次モーメントが小さい方の軸、つまり「弱い」軸を中心に座屈します。 これは、両軸の拘束力が等しいことを前提としています。 ユニバーサルコラム(UC)の断面が圧縮される場合を考えてみましょう。
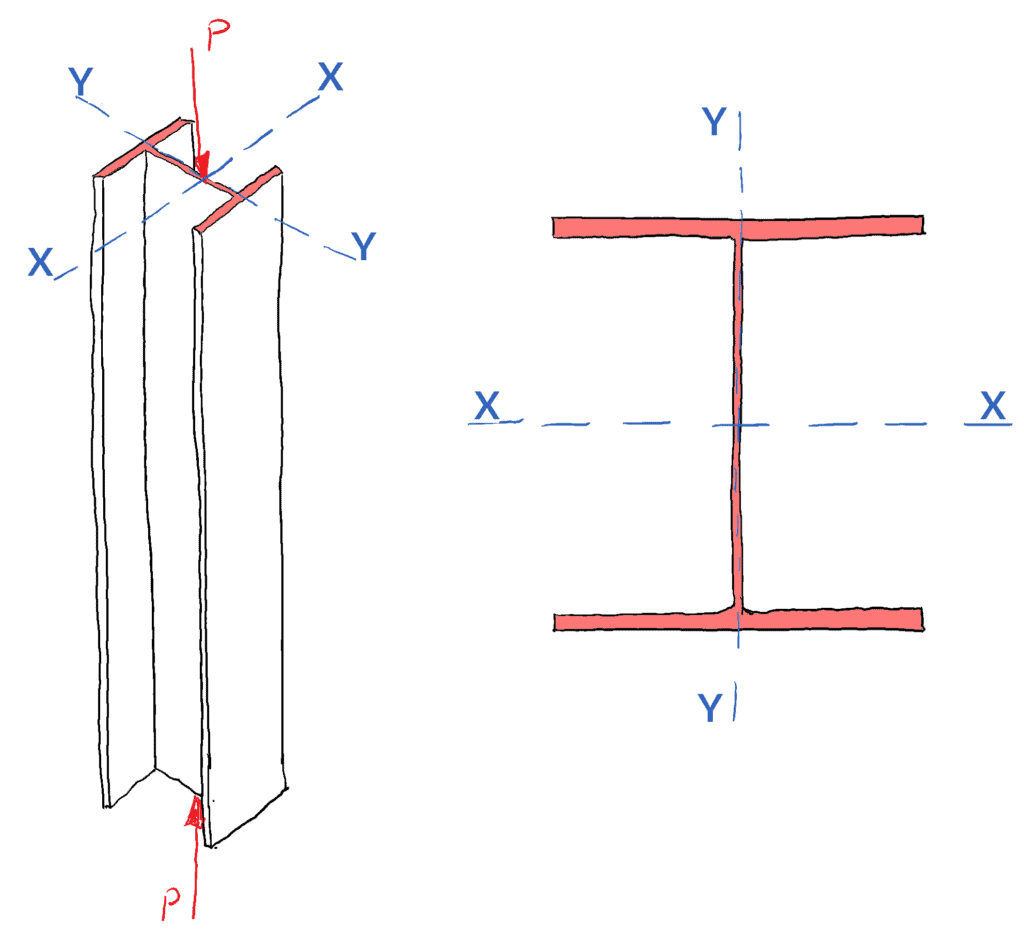
X-X軸。 は大原則軸 (面積の二次モーメントの最大値を持つ軸 – Mohr の円の研究から覚えているかもしれません) であり、これはより強い軸であるため、柱はまず小原則軸または Y-Y 軸を中心に座屈します。
柱構造の座屈荷重を検討する際には、断面形状が重要な役割を果たすため、長軸と短軸を評価して座屈の臨界軸を決定する必要があります。
5.0 臨界応力
📌 臨界応力とは、臨界荷重下での断面における平均軸方向応力のことです。
![]()
ここで、旋回半径を定義します。 と定義します。
![]() {align*}
{align*}
このことから、臨界応力を次のように書くことができます。
![]()
最後に、Slenderness Ratioを次のように定義します。
![]()
スレンダーネス比は、柱の形状や座屈のしやすさを表す非常に有効な指標です。 スレンダネス比が高いほど座屈しやすいことを示しています。 柱の形状や座屈のしやすさを表す指標としては、細長比が大きいほど座屈しやすい。
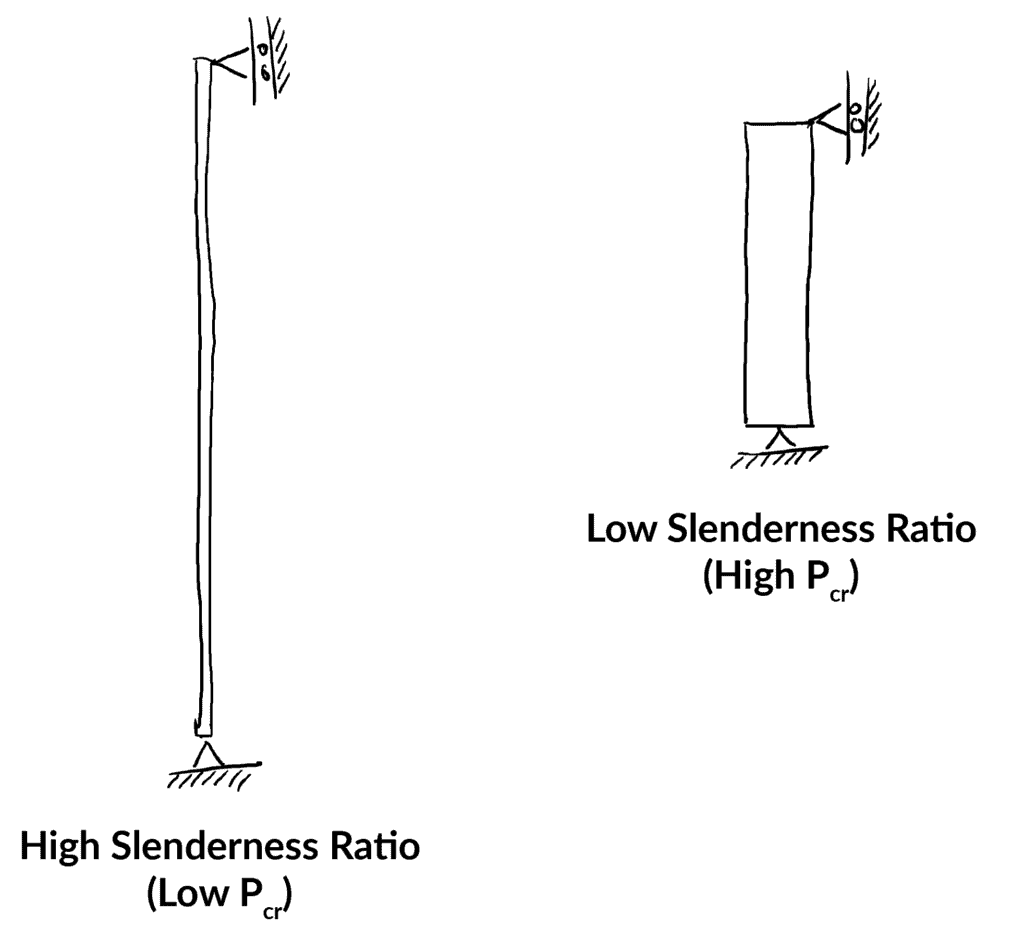
そのため、限界応力の式は、スレンダネス比の関数として次のように書くことができます。
![]()
あるヤング率の値に対する限界応力とスレンダーネス比をプロットすると、次のようになります。
与えられたヤング率の値に対する限界応力とスレンダーネス比をプロットすると、与えられたスレンダーネス比に対する平均軸方向応力の安全な範囲を示すオイラー曲線が得られます(または、与えられた軸方向応力に対するスレンダーネス比の安全な範囲)。
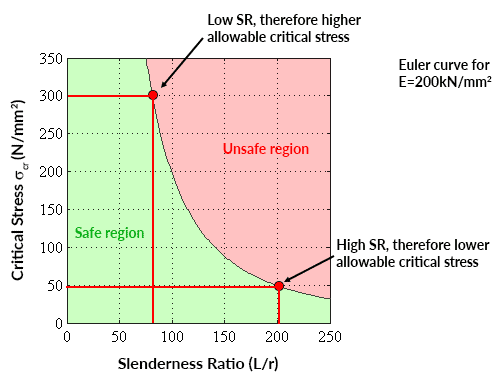
📌 オイラー曲線は、材料の降伏応力以下の臨界応力の場合にのみ有効です
6.0 コラムの有効長
この記事で見る最後の概念は、コラムの有効長です。 コラムの有効長、![]() は、たわみ曲線/形状の変曲点間の長さです(変曲点に到達するまで形状を延長しなければならない場合でも、後述します)。
は、たわみ曲線/形状の変曲点間の長さです(変曲点に到達するまで形状を延長しなければならない場合でも、後述します)。
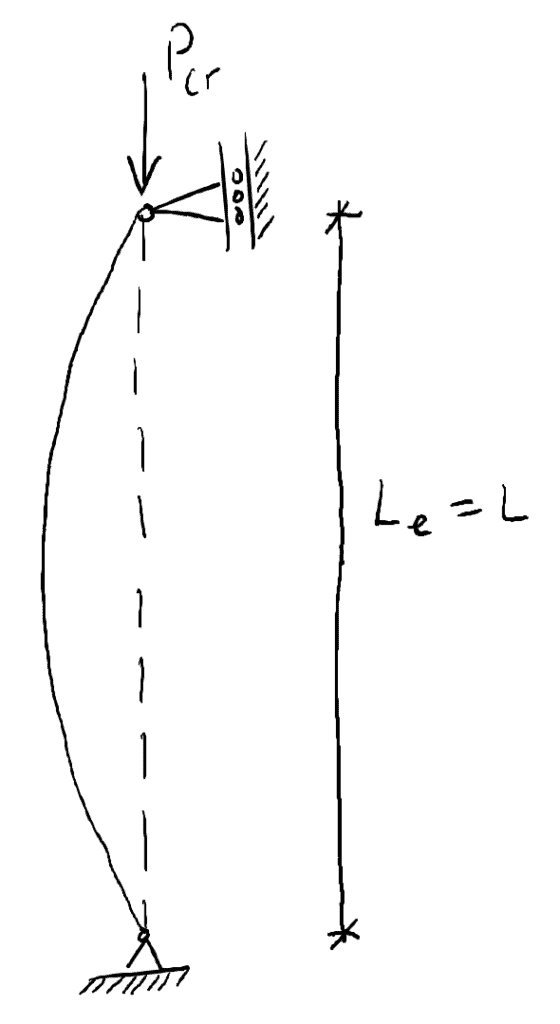
柱の根元に固定されたサポートがあり、上部には横方向の拘束がない(fixed-free)柱について考えてみましょう。 根元では回転は起こりません。 たわみ形状に2つの変曲点を得るためには、延長しなければなりません…
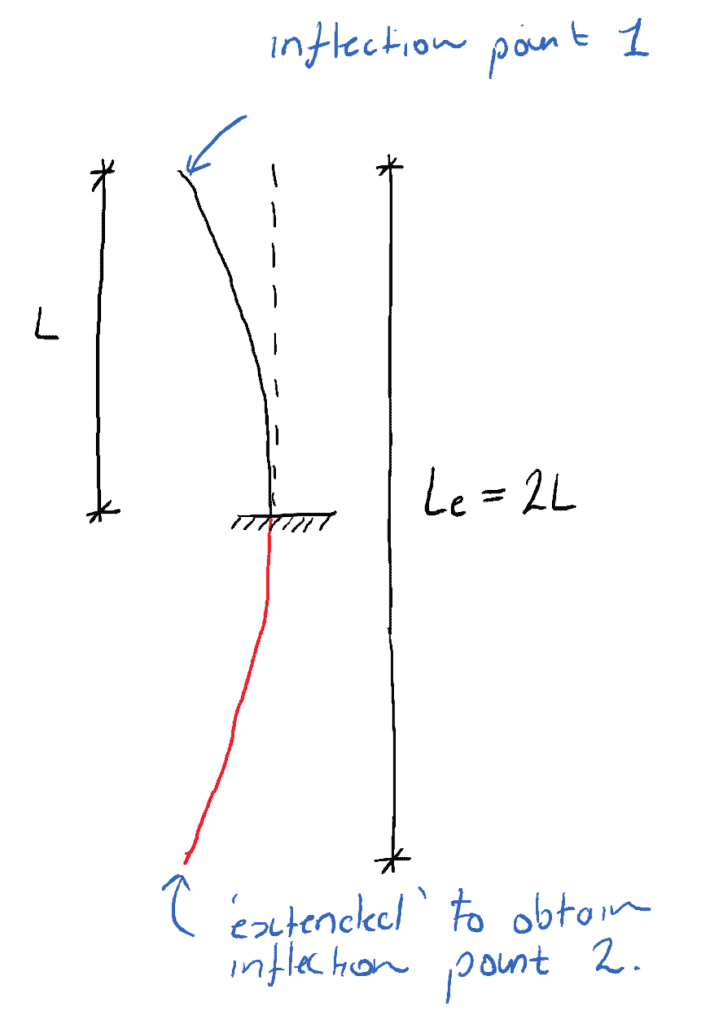
たわみ形状の「想像上」の赤い部分は、変曲点番号2を提供するために必要な延長です。
📌 有効長についての別の考え方は、同等のピン留めされた端部の柱の長さです。
有効長の議論を終える前に、限界荷重の一般的な表現を次のように定義することができます。
![]()
ここで、有効長係数を導入すると。 ![]()
![]() となり、臨界荷重を実効長さ因子の関数として表すことができます。
となり、臨界荷重を実効長さ因子の関数として表すことができます。
![]()
Subscribe for Updates
新しいチュートリアルやコースの上陸時に通知を受ける



