等価分数

等価分数は、見た目が違っていても、同じ値を持っています。

以下の分数は、実際には同じです：

12 = 24 = 48

なぜ同じなのでしょうか？ 上と下の両方に同じ数を掛けたり割ったりすると、分数はその値を維持するからです。

覚えておくべきルールは次の通りです：

「掛け算や割り算で下を変えると、上にも同じことをしなければならない」

これらの分数が本当に同じである理由は次の通りです。

	×。 2		× 2	です。
1	=	2	=	4
2		3		4	8
	×2		td 2

そして、視覚的には次のようになります。

1/2		2/4		4/8
	=		=

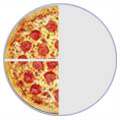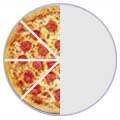「数直線上の分数」を参照してください。…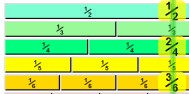

…多くの等価分数を示しています。

また、等価分数の多くの例を示した「分数の表」もご覧ください。

Dividing

ここでは、さらにいくつかの等価な分数を、今度は分割することによって示します。

td

	÷3		÷6
18	=	6	=	1td
36		12		2
	÷ 3		÷ 6

割る数の選択は慎重に行ってください。

分割する数を慎重に選び、結果（上下とも）が整数になるようにします。

これ以上進まなくなるまで割り続けると、分数を簡略化したことになります（できるだけシンプルにしたことになります）。