10.2 – 自己相関と時系列法

重回帰モデルの「独立性」条件が失敗する一般的な方法の1つは、サンプルデータが時間をかけて収集され、回帰モデルが時間的傾向を効果的に捉えることができない場合です。 このような状況では、モデル内のランダムエラーが時間的に正の相関を持つことが多く、ランダムエラーが互いに独立している場合よりも、それぞれのランダムエラーが前のランダムエラーと類似している可能性が高くなります。 この現象は、自己相関（または系列相関）として知られており、モデルの残差を時間に対してプロットすることで検出できることがあります。

時系列とは、同じ変数を時間をかけて測定した一連の測定値のことです。 通常、測定は、毎月または毎年など、等間隔の時間に行われます。 まず、時系列で測定されたy変数がある場合の問題を考えてみましょう。 例えば、地球の気温を表すy変数があり、毎年測定が行われているとします。 時系列で測定された値であることを強調するために、通常の「i」ではなく「t」を添え字として使用しています。 自己回帰モデルとは、ある時系列の値をその時系列の過去の値に回帰させたもので、例えば、\(y_{t}\)on \(y_{t-1}\):

この回帰モデルでは、前の時系列の応答変数が予測変数となり、誤差は単純な線形回帰モデルの誤差を想定しています。 自己回帰の次数は、現時点での値を予測するために使用される系列の直前の値の数です。 つまり、先行するモデルは1次の自己回帰であり、AR(1)と書かれます。

過去2年間の世界の気温の測定値（˶{t-1},y_{t-2}˶）を用いて、今年の気温（˶{t-1},y_{t-2}˶）を予測したい場合、そのための自己回帰モデルは次のようになります。

このモデルは、時刻$t$の値が、時刻\(t-1\)とathy(t-2\)の値から予測されることから、AR(2)と書かれる2次自己回帰モデルとなります。 より一般的には、AR(k)と表記される、\(t-1,t-2,˶‾᷄ -̫ ‾᷅˵)オーダーの自己回帰は、任意の時間tにおける系列の値が、時間\(t-1,t-2,˶‾᷅˵)における値の(線形)関数である重回帰です。

自己相関と部分自己相関

時系列の2つの値の間の相関係数は自己相関関数（ACF）と呼ばれます。 ラグ1の自己相関(上図ではk=1)は、1期間離れた値の間の相関です。

ACFは、ある時刻tの観測値とそれ以前の時刻の観測値との間の線形関係を測定する方法です。 AR(k)モデルを仮定した場合、\(y_{t}\)と\(y_{t-k}\)の間の関連性のみを測定し、その間にある確率変数（つまり、\(y_{t-1},y_{t-2},\ldots,y_{t-(k-1 )}\）の線形的な影響をフィルタリングしたい場合、時系列の変換が必要になります。

PACFは、自己回帰モデルの次数を特定するのに最も有効です。 具体的には、サンプルの部分自己相関が0から有意に異なる場合、\(y_{t}\)の予測因子となるラグ付きの項を示しています。 ここで重要なのは，順序の選択に意味があるということです。 例えば、過去2年間の毎日の血圧測定値があるとします。 血圧のモデル化には、AR(1)またはAR(2)モデルが適切であることがわかるかもしれません。

例 1: Google データ

データ セット (google_stock.txt) は、2005 年 2 月 7 日から 2005 年 7 月 7 日の間の Google 株式 1 株の終値である n = 105 個の値で構成されています。 このデータセットを分析して、自己回帰モデルの次数を確認します。

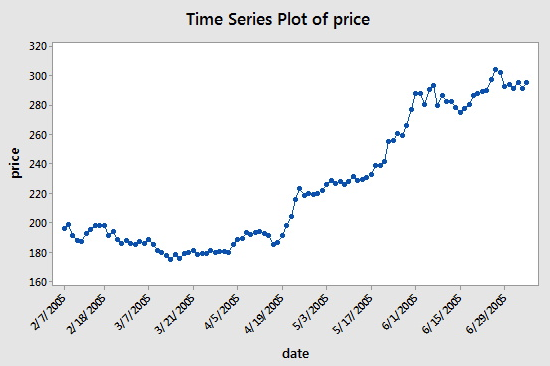
連続した値がかなり密接に追随しているように見えることから、自己回帰モデルが適切である可能性が示唆されます。

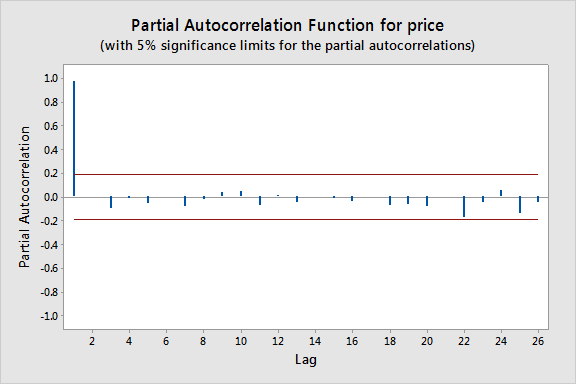
ここでは、ラグが 1 のときに顕著なスパイクがあり、それ以降のラグではスパイクがかなり少ないことがわかります。

大きな値を決定するために、このプロットに近似境界を構築することもできます (上のプロットの赤い線で示されています)。 近似的な有意差の範囲は\(1-˶‾᷅᷅˵)で与えられます。 このいずれかの境界の外側にある値は、自己回帰プロセスを示しています。

次にlag-1価格変数を作成し、このlag-1変数に対する価格の散布図を検討します。

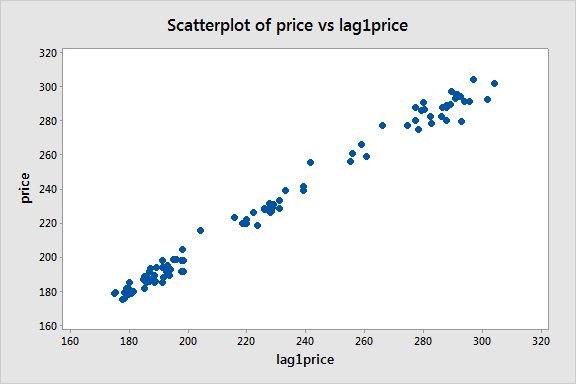
強い線形パターンがあるように見え、一次自己回帰モデル

が有用であることが確認されました。

Example 2: 地震のデータ

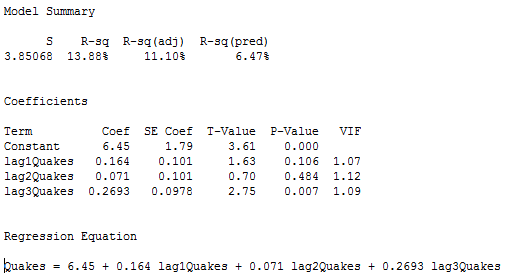
yt=n=100年間のリヒタースケールで7以上の世界的な地震の年間発生数とします（データはhttps://earthquake.usgs.govから入手したearthquakes.txt）。 下の図は、このデータセットの時系列プロットです。

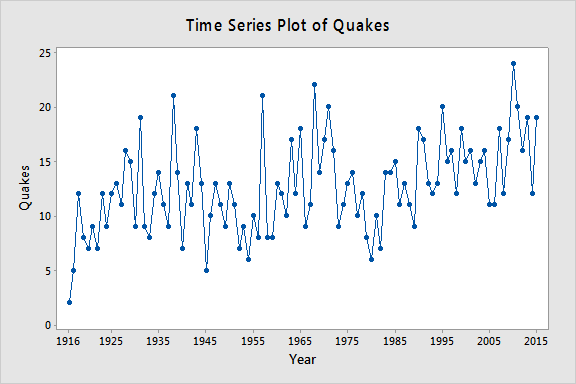
以下のプロットはPACF（部分自己相関関数）のプロットで、ラグ1とラグ3に顕著な部分自己相関があることから、3次の自己回帰が必要であると解釈できます。

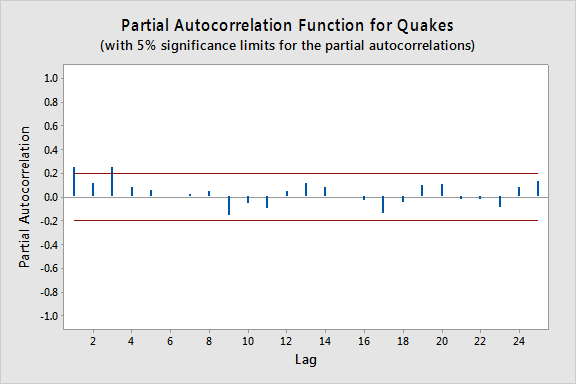
次に、地震の数を応答変数、ラグ-1、ラグ-2、ラグ-3の地震を予測変数とした重回帰を行いました。