32 ビット ALU
回答欄に数値を入力する際には、整数（1000、0x3E8、0b1111101000）、浮動小数点数（1000.役に立つリンク:
- Jadeの紹介
- 標準セルライブラリ
問題1. Design Problem: 32-bit Arithmetic and Logic Unit以下の説明を参照してください。以下のJadeインスタンスを使用して、デザインを入力してください。 このデザイン問題を完了するには、/alu/aluモジュールを選択し、Jadeツールバーをクリックして、内蔵のtesterwillは、期待される出力と実際の出力の間の不一致を報告するか、または、あなたのデザインが正しい場合、それはテストが合格したと記録します.{ “shared_modules”: , “hierarchical”: “true”, “parts”: , “tools”: , “editors”: , “edit”: “/alu/alu”, “required_tests”: }この実習では、ベータ・プロセッサのALU（arithmetic and logic unit）を作ります。 ALUは、2つの32ビット入力（”A “と “B “と呼びます）を持ち、1つの32ビット出力を生成します。 まず、ALUの各部分を独立した回路として設計し、それぞれが32ビットの出力を出すようにします。 そして、これらの出力を1つのALUの結果にまとめます。回路を設計する際には、最適化できる3つの要素があります。
- 最大性能（最小レイテンシ）の設計
- 最小コスト（最小面積）の設計
- 最良のコスト/性能比（最小面積*レイテンシ）の設計
幸いなことに、3つすべてを同時に行うことが可能な場合が多いのですが、回路の一部では、ある種の設計上のトレードオフを行う必要があります。 回路を設計する際には、3つの要素のうちどれが最も重要であるかを選択し、それに応じて設計を最適化する必要があります。 スタンダードセルライブラリ & ゲートレベルシミュレーションこの研究室のビルディングブロックは、ロジックゲートのライブラリから来ています。ICメーカーは、モスフェットや配線を作成するために使用されるマスク層の詳細なジオメトリを気にすることなく、顧客が簡単に設計できるように、「スタンダードセルライブラリ」やさまざまな設計ツールを持っていることがよくあります。
2入力、3入力、4入力のAND、OR、NAND、NORゲート
2入力のXOR、XNORゲート
2:1および4:1マルチプレクサー
Dレジスタ、Dラッチ
各ゲートの適切な接続の詳細については、ライブラリのドキュメントを参照してください。
ゲートレベルで設計しているので、（トランジスタや電圧ではなく）ゲートと論理値のみを知る高速シミュレーターを使用することができます。 ゲートレベルのシミュレータは、スタンダードセルライブラリのゲートプリミティブのみをサポートしているため、デザインにはモスフェット、抵抗、コンデンサなどは含まれません。入力は電圧で指定されますが (他のシミュレータとのネットリストの互換性を保つため)、ゲートレベルシミュレータは、デザインファイルの最初に指定された vil と vih のしきい値を使用して、電圧を 3 つの可能な論理値のいずれかに変換します。
1 logic high (vihしきい値以上の電圧)
X unknown or undefined (しきい値の間の電圧、または未知の電圧)
4番目の値「Z」は、どのゲート出力によっても駆動されていないノードの値を表すために使用されます。g., 4つ目の値 “Z “は、どのゲート出力によっても駆動されていないノードの値を表します。) 次の図は、これらの値が波形表示されている様子を示しています。
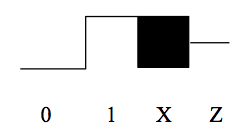
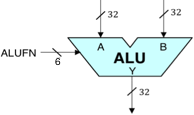今回製作する32ビットALUは、この後の研究室で取り組むベータプロセッサの構成要素となります。 このALUの論理記号を右に示します。 これは、2つの32ビットのデータワードAとBを入力とし、AとBの入力に対して指定された算術関数または論理関数を実行して32ビットの出力Yを生成する組み合わせ回路である。 実行される特定の機能は6ビットの制御入力FNで指定され、その値は次の表のように機能をコード化します。
| FN | Operation | Output Value Y |
|---|---|---|
| 00-!011 | CMPEQ | Y = (A == B) |
| 00-101 | CMPLT | Y = (A < B) |
| 00-!111 | CMPLE | Y = (A ≤ B) |
| 01–0 | 32ビットADD | Y = A + B |
| 01-?-1 | 32ビットSUBTRACT | Y = A – B |
| 10abcd | ビットワイズ・ブーリアン | Y = Fabcd(A,B) |
| 11–00 | ロジカルシフトレフト(SHL) | Y = A << B |
| 11-!-01 | ロジカル・シフト・ライト（SHR） | Y = A >> B |
| 11–11 | Arithmetic Shift right (SRA) | Y = A >> B (sign extended) |
なお、6ビットのFN入力に適切な値を指定することで、ALUは様々な処理を行うことができます。 ALUは、6ビットのFN入力に適切な値を指定することで、Betaプロセッサが必要とする様々な算術演算、比較、シフト、ビットごとのブール演算の組み合わせを行うことができます。
| Bi | Ai | Yi |
| 0 | d | |
| 0 | 1 | c |
| 1 | 0 | b |
| 1 | a |
ビット単位のブール演算はFN=10で指定されています。 この場合、FNの残りのビットabcdは、右図のように、Yの各ビットがAとBの対応するビットによってどのように決定されるかを記述した真理値表の項目として扱われます。3つの比較演算は、それぞれブール値を出力します。 これらの場合、Yはすべて0で、下位ビットのYは32ビットのAとBのオペランドの比較結果を反映して0または1になります。ALUの設計は、以下のように、算術演算、比較、ブール演算、シフト演算のサブシステムに分けてアプローチすることができます。
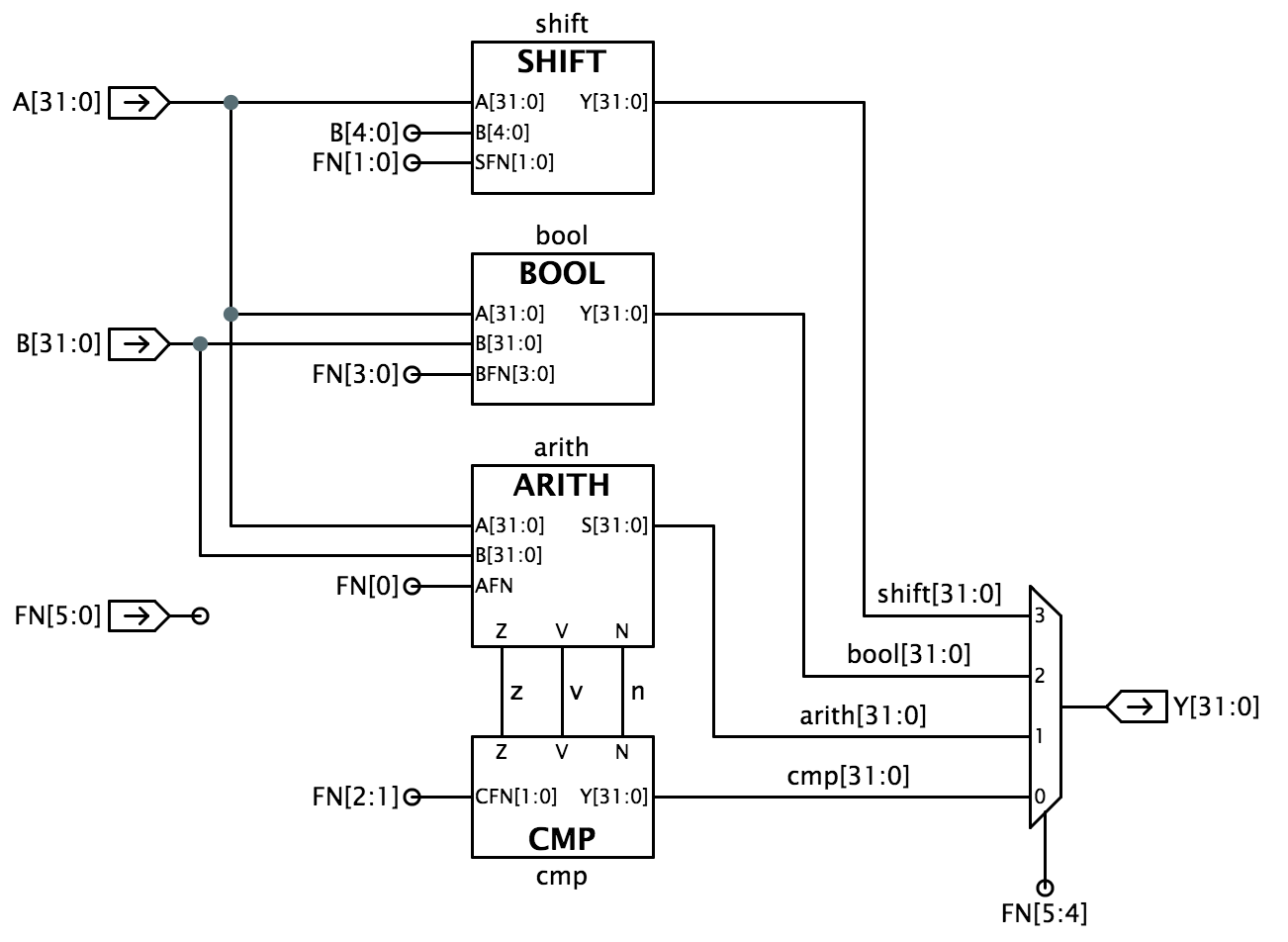
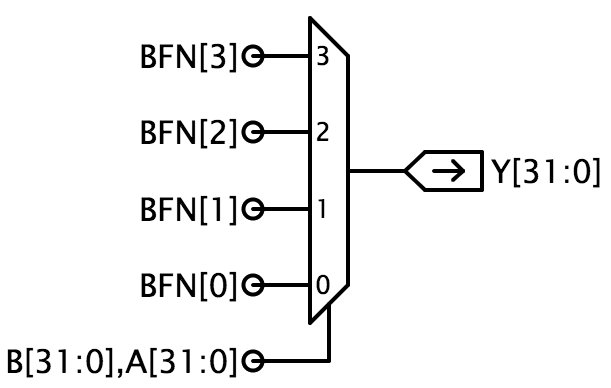提案された実装では、4対1のマルチプレクサ(mux4)のコピーを32個使用しています。BFNは実行する演算をエンコードし、AとBはマルチプレクサのセレクト入力にフックされます。
次の表は、テスト用治具で使用されるBFN制御信号のいくつかのエンコーディングを示しています(我々の典型的なBetaimplementationでも使用されます)。
| 動作 | BFN |
|---|---|
| AND | 1000 |
| OR | 1110 |
| XORtd | 0110 |
| “A” | 1010 |
| 比較 | LSBの計算式th | CFN |
|---|---|---|
| A = B | LSB = ˶(Z˶) | 01 |
| A < B | LSB = “\\” | 10 |
| A ≤ B | LSB = “⏺️”(Z + (N ⏺️) | 11 |
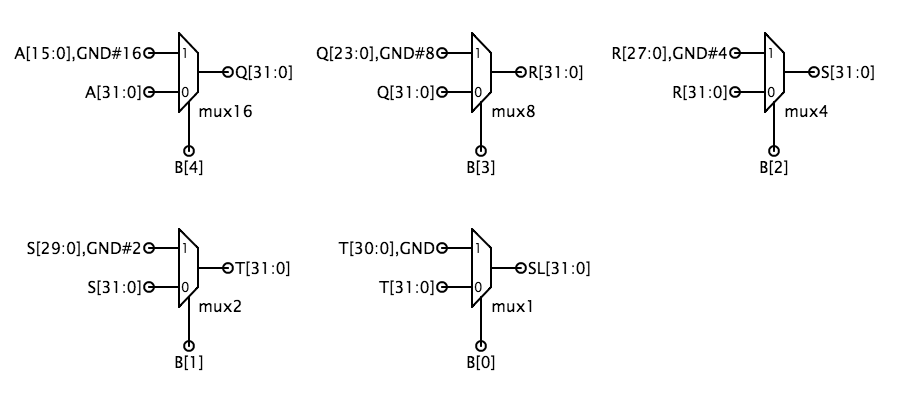
| 操作 | SFN |
|---|---|
| SHL (左シフト) | 00 |
| SHR (シフト 右シフト） | 01 |
| SRA（符号拡張による右シフト） | 11 |
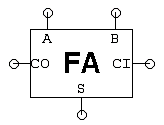
- 全加算器の1つのテストベクターは、3つの入力値（A、B、CIに各1つ）と2つの出力値（S、CO）で構成されています。 テストを実行するには、現在のテストベクターからの入力値を被試験デバイスに適用し、実際の出力値をテストベクターに記載されている期待値と比較します。 このプロセスは、すべてのテストベクターが使用されるまで繰り返されます。 全加算器の内部回路について何も知らないと仮定して、その機能を網羅的にテストするには、いくつのテストベクタが必要でしょうか。 全加算器を徹底的にテストするためのテスト ベクトルの数は？
- 64 個の入力 (2 つの 32 ビット入力オペランド、CIN は下の図のようにグランドに接続されていると仮定) と 32 個の出力 (32 ビットの結果) を持つ 32 ビット加算器を考えます。 内部の回路については何も知らないので、入力の組み合わせによっては間違った結果が出る可能性を排除できないとします。 つまり、2＋3で正しい答えが出たからといって、2＋7でどのような答えが出るのか、結論を出すことはできないのです。 100nsごとに1つのテストベクターを適用できるとしたら、加算器を網羅的にテストするにはどれくらいの時間がかかるでしょうか。 32 ビット加算器を網羅的にテストする時間は？
- 明らかに、入力値のすべての組み合わせを試して32ビット加算器をテストすることは、良い計画ではありません。 以下に、32 ビットのリップルキャリー加算器の回路図を示します。
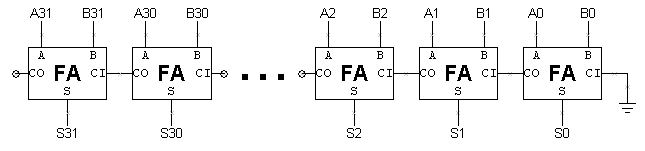右隣のビットからのキャリーインを除いて、加算器の各ビットは独立して動作しています。 この観察結果を利用して、加算器をビットごとにテストすることができ、少し考えれば、実際にこれらのテストの多くを並行して実行することができます。 この場合、加算器が2 + 3に対して正しい答えを出したという事実は、実際に2 + 7に対して出す答えについて多くのことを教えてくれます。 加算器のビット0とビット1で行われる計算はどちらも同じなので、2＋3の答えが正しければ、2＋7の答えの下位2ビットも正しいことになります。 そこで、リップルキャリー加算器をテストする計画は、各全加算器を独立してテストすることです。 ビットNをテストするときは、テストベクターから直接AとBを設定します。 CIを0にしたい場合、AとBはどのような値にすればよいでしょうか。 CIを1にしたい場合は？ CIの値については何も仮定できないとする。 C=0にするためのAとBの値？ A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 C=1にするためのAとBの値は？ A=0, B=0 A=1, B=0 A=0, B=1 A=1, B=1 この方法では、加算器の偶数ビットを1組のテストベクターで並列にテストし、奇数ビットを別のテストベクターで並列にテストすることができます。 ここでは、32ビットのリップルキャリー加算器の各FAの入力値のすべての組み合わせをテストするための10個のテストベクターのセットを紹介します。
ビット0、2、… ビット1、3、…。 A B A=0, B=0, CI=0 A=0, B=0, CI=0 0x00000000 0x00000000 A=1, B=0, CI=0 A=0, B=0, CI=0 0x555555 0x00000000 A=0, B=1, CI=0 A=0, B=0, CI=0 0x00000000 0x555555 A=1, B=1, CI=0 A=0, B=0, CI=1 0x555555 A=0, B=0, CI=0 A=1, B=0, CI=0 0xAAAAAAAA 0x00000000 A=0, B=0, CI=0 A=0, B=1, CI=0 0x00000000 0xAAAAAAAA A=0, B=0, CI=1 A=1, B=1, CI=0 0xAAAAAAAA A=1, B=0, CI=1 A=1, B=0, CI=1 0xFFFFFFFF 0x00000001 A=0, B=1, CI=1 A=0, B=1, CI=1 0x00000001 0xFFFFFFFF A=1,B=1,CI=1 A=1,B=1, CI=1 0xFFFFFFFF - コンペアユニットの入力のうち3つ（Z、V、N）は、A-Bを計算する減算モードで動作する加算器/減算器から来ています。
| Bi | Ai | Yi |
| 0 | 0 | d |
| 0 | 1 | c |
| 1 | 0 | b |
| 1 | 1 | a |
ALUの命令で見たように。ビット単位のブール演算はFN=10で指定されています。 この場合，FNの残りのビットabcdは，右図のように，Yの各ビットがAとBの対応するビットによってどのように決定されるかを記述した真理値表の項目として扱われます。以下に示す各ブール演算\(F(A,B)\)について，Boolユニットが必要な演算を行うようにFNの設定を決定します。 AND(A,B): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 or(A,B): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 XOR(A,B): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 NAND(A,B): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 nor(a,b): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 xnor(a,b): FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 A: FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 B: FN= 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
div